课程地址：https://www.xuetangx.com/course/nju0802bt/14363483

课程回放：https://www.xuetangx.com/learn/nju0802bt/nju0802bt/14363483/video/26163005

课程讨论：https://www.xuetangx.com/learn/nju0802bt/nju0802bt/14363483/forum

教材地址：https://cs.nju.edu.cn/zhouzh/zhouzh.files/publication/MLbook2016.htm

试题备份：https://xuwp.top/Zhihua-Zhou-Machine-Learning-Prelim-Questions.html

绪论

科学、技术、工程、应用各解决什么问题？

科学：是什么？为什么？

技术：怎么做？

工程：怎么做得多、快、好、省？

应用：怎么用？

机器学习

经典定义：利用经验改善系统自身的性能（T. Mitchell, 1997）

经验在计算机系统中以数据形式存在，因对数据分析的需求，从而产生了智能数据分析理论和方法。“智能”前缀是为了与数学家、统计学家利用数理统计方法进行数据分析相区别，其强调人工智能学者利用计算机进行数据分析。

典型的机器学习过程

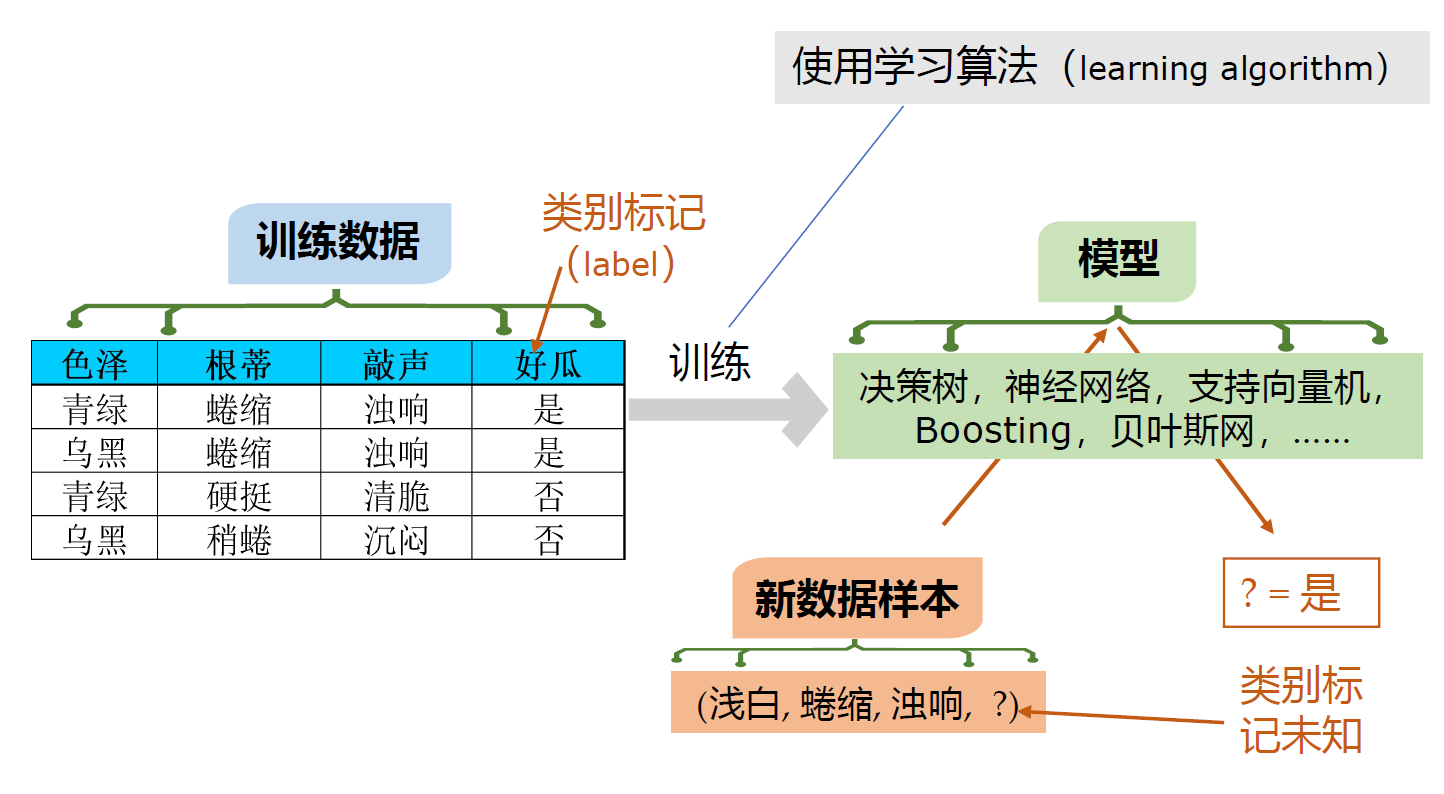
在训练数据上，使用学习算法，经训练，得到模型，输入新数据，产生输出。

从数据中产生的东西，可以认为是一个神经网络，甚至是一条规则，都可以宽泛地统称为“模型”。

David Hume(?)：适用于全局的叫模型，适用于局部的叫模式。

计算学习理论

机器学习具有坚实的理论基础：Leslie Valiant建立的计算学习理论（Computational learning theory），其中最重要的模型是PAC（Probably Approximately Correct，概率近似正确）learning model（Leslie Valiant, 1984）。

其基础表达式：

在机器学习中解释为：以很高的概率得到很好的模型。

Q：为什么要有$\epsilon$和$\delta$，而不是$P\left(\left\vert f(\boldsymbol{x}) - y \right\vert= 0\right)= 1$呢？

A：从人工智能基本概念的角度，对于确定性的知识，我们可以通过确定性推理方法，在多项式时间内得到确定性结果。机器学习往往处理那些带有不确定性的知识及它们的组合，因为知识带有不确定性，所以我们的结果一定带有可信度，因此需要引入$\epsilon$。

从计算的角度，机器学习往往处理$NP$问题，如果模型$f(\cdot)$每次都以$P=1$的概率预测出最佳答案$y$，即在多项式时间内解决掉了问题，那么就意味着我们构造性地证明了$P=NP$，因为$P=NP$尚未被证明，因此需要引入$\delta$。

基本术语

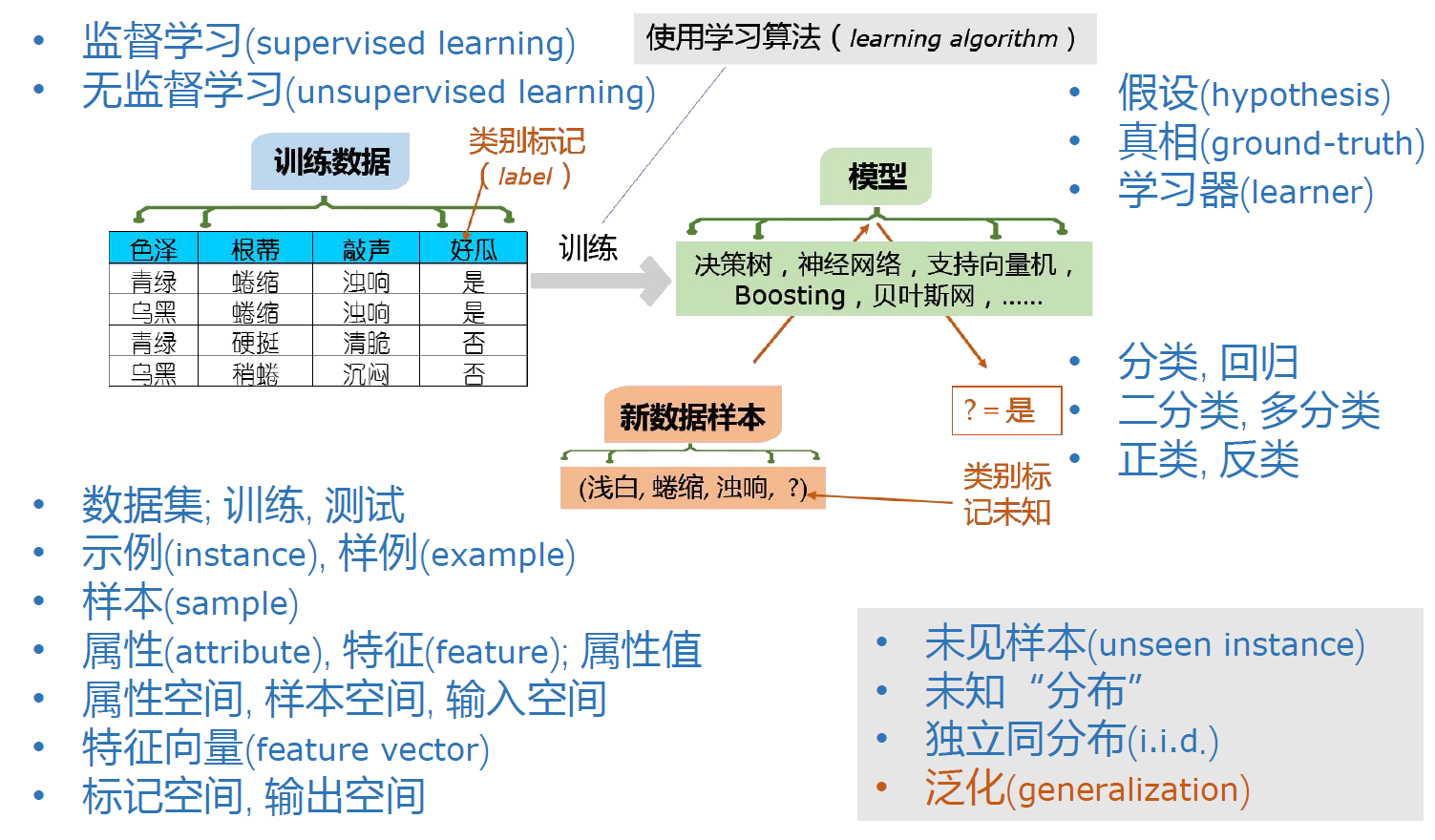
输入部分

数据集：dataset，如图左侧的表

训练：train，建立模型的过程

测试：test，向模型传入数据，根据数据的label判断模型的结果正确或错误

示例：instance，如（青绿，蜷缩，浊响）

样例：example，如（青绿，蜷缩，浊响，是）

样本：sample，有时指样例，如（青绿，蜷缩，浊响，是）；有时指数据集，如图左侧的表

属性/特征：attribute/feature，如色泽

属性值：attribute value，如青绿

属性空间/样本空间/输入空间：attribute space/sample space/input space，由属性所张成的空间，如轴为青绿、蜷缩、浊响的三维空间

特征向量：feature vector，示例在属性空间中所形成的向量

模型部分

假设：hypothesis，训练得到的模型，即PAC模型中的$f(\boldsymbol{x})$

真相：ground-truth，即PAC模型中的$y$

学习器：learner，在训练数据上使用学习算法经训练产生的东西，可以宽泛地认为是“模型”，如“分类器”

输出部分

分类：classification，输出是离散的

二分类：binary classification，可能输出的基数为2

多分类：multiclass classification，可能输出的基数大于等于2，可以分解为若干个二分类问题

回归：regression，输出是连续的

正类：positive class，对输出进行划分，我们需要的部分定义为正类，如“好瓜”中的是

负类：negative class，对输出进行划分，我们不需要的部分定义为负类，如“好瓜”中的否

学习任务

监督学习：supervised learning，样例中含有label的学习任务，主要任务：分类、回归

无监督学习：unsupervised learning，样例中不含label的学习任务，主要任务：聚类（离散）、密度估计（连续）

基本假设

未见样本：unseen instance，不在训练数据中的样本

未知分布：unknown distribution，所有的数据所服从的分布

独立同分布：i.i.d. (independent and identically distributed)，样本服从同一分布，并且互相独立。只有满足独立同分布才能应用统计学的基本原理（大数定律），用频率逼近概率。

泛化：generalization，对新数据处理的能力，即PAC模型中的$\epsilon$能做到多小，当$\epsilon < 0.5$（比随机猜测准）时，可以努力去优化模型的性能。

归纳偏好

归纳偏好/偏置（Inductive Bias）：机器学习算法在学习过程中对某种类型假设的偏好。

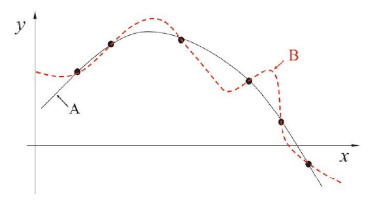
如图，当两种模型（类型假设）都能解释训练数据时，哪种模型更好？此时需要由算法的归纳偏好决定。因此机器学习算法的归纳偏好是否与问题本身匹配，直接决定算法取得的性能。

奥卡姆剃刀（Occam’s razor）准则：一个典型的归纳偏好，其最流行的表述方式为：“若非必要，勿增实体”，另外还有一种表述为“若有多个假设与观察一致，则选最简单的那个”。

但因“简单”这个标准比较宽泛，所以如何确定哪个假设更“简单”有很多种不同角度的实现方式。

NFL定理

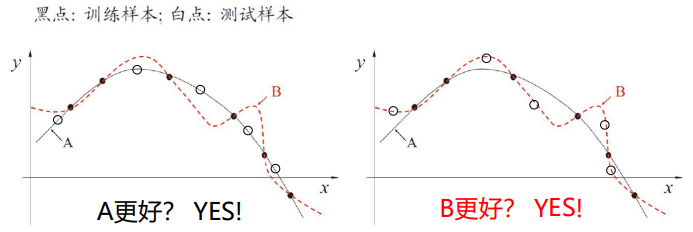
NFL定理（No Free Lunch Theoren）：一个算法$\mathfrak{L}_a$若在某些问题（左图）上比另一个算法$\mathfrak{L}_b$好，必存在另一些问题（右图），$\mathfrak{L}_b$比$\mathfrak{L}_a$好。

NFL定理的重要前提：所有问题出现的机会相同，或所有问题同等重要。

因此，机器学习中没有“更好的算法”，只有“在这个问题上更好的算法”！

模型评估与选择

泛化能力

错误率低、精度高、召回率高，都可以作为好模型的标准，与NFL定理类似，没有“好标准”，只有“在这个问题上的好标准”

泛化能力（generalization ability）：模型在未见样本上表现好。

过拟合和欠拟合

经验误差/训练误差（empirical error/training error）：学习器在训练集上的误差

泛化误差（generalization error）：学习器在新样本上的误差

因为过拟合现象的存在，经验误差与泛化误差并不是越小越好。

过拟合（overfitting）：学习器把训练样本自身的一些特殊性质当做了所有样本都会有的一般性质。

欠拟合（underfitting）：学习器尚未学好训练样本自身的性质。

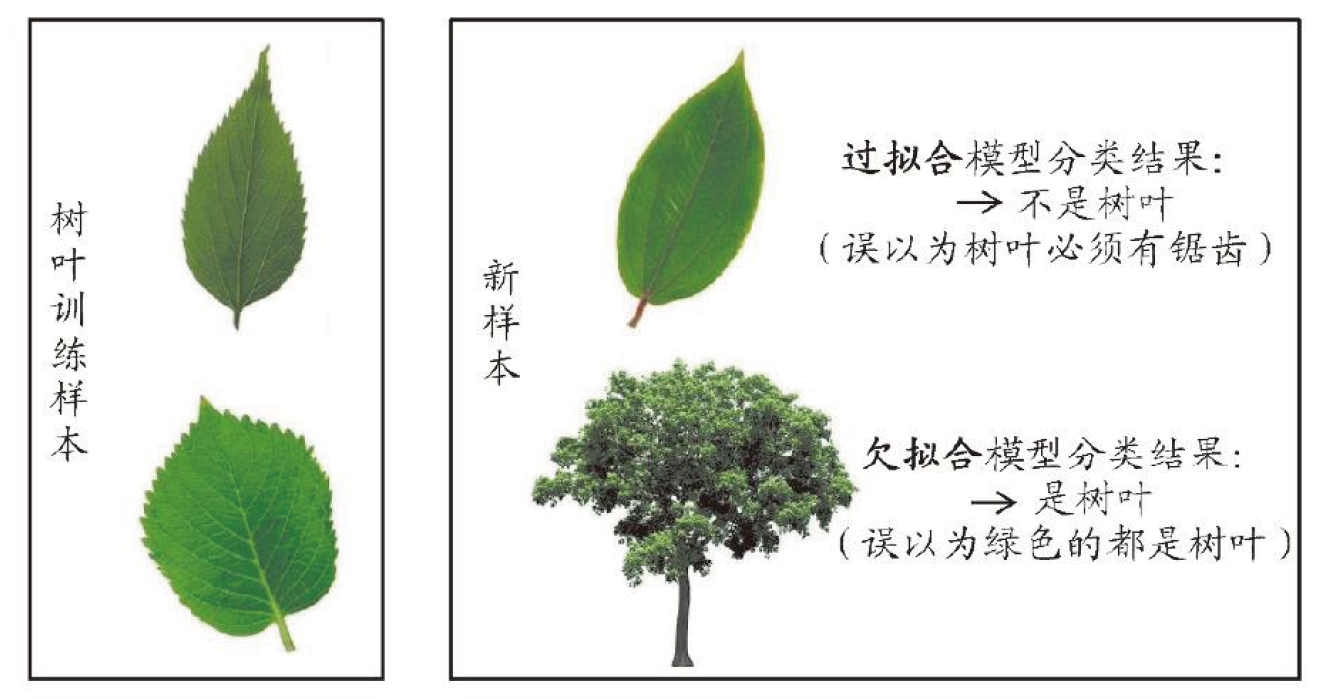
过拟合、欠拟合的直观类比

所以，对于具体机器学习算法，明白了其用什么方法缓解overfitting，这种方法在什么时候失效，就明白了这个机器学习算法的应用场景。

三大问题

如何进行模型选择，有三个关键问题：

  • 如何获得测试结果？
  • 如何评估性能优劣？
  • 如何判断实质差别？

解决这三个方面的问题，有一些经典的方法/标准，分别为：

  • 评估方法：对学习器的泛化误差进行量化
  • 性能度量：衡量模型泛化能力的评价标准
  • 比较检验：比较模型在统计意义上的表现

三者的工作方式为：对于某个学习器，使用某种评估方法，测得某个性能度量结果，比较检验这些结果。

评估方法

注：这一节提到的“测试集”，用“验证集”表述更好。

Q：怎么获得测试集？测试集应与训练集“互斥”。

A：对数据集进行适当的处理，从中产生训练集和测试集。

常见方法：留出法（hold-out）、交叉验证法（cross validation）、自助法（bootstrap）

留出法

直接将数据集划分为两个互斥的集合

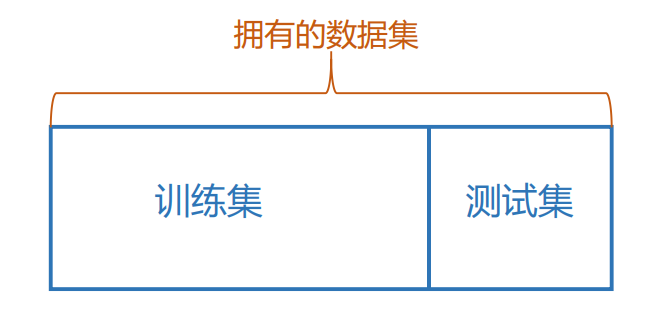
注意：

  • 保持数据分布的一致性，如分布采样/分层采样（stratified sampling）
  • 多次重复划分，如100次随机划分
  • 测试集不能太大、不能太小（$\frac{1}{5}$~$\frac{1}{3}$）

Q：如果有一些数据，每次重复划分都在训练集里，永远没有被用作测试怎么办？

A：使用k折交叉验证，可以保证所有数据都成为过测试数据。

k折交叉验证

将数据集（共m个样本）划分为k个大小相似的互斥子集，每次用k-1个子集的并集作为训练集，余下的那个子集作为测试集。

留一法（leave-one-out, LOO）：k=m时的k折交叉验证，即每1个样本都被用作其余m-1个样本的测试数据一次。

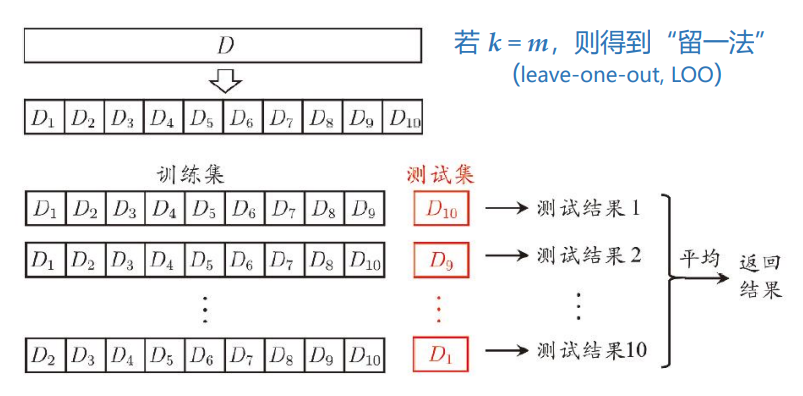
10折交叉验证

将m个样本划分为k个子集的方式有很多，为了减小因划分方式的不同而引入的差别，通常要重复p次不同的划分方式，最终的评估结果为“p次k折交叉验证”的均值，如“10次10折交叉验证”。

k折交叉验证中，将k-1个子集训练出的Model，视为用全部数据集训练出的Model进行评估，即$\widetilde{M}_k=M_{k-1}$。

Q：有没有什么方法，既可以直接得到$M_k$，又有剩余的数据进行测试呢？

A：自助法

自助法

自助法以自助采样法（bootstrap sampling）为基础（Efron and Tibshirani, 1993），其内容为：

给定数据集D（共m个样本）和数据集$D^{\prime}$（初始共0个样本），重复m次以下操作：从D中随机选中1个样本，复制进$D^{\prime}$。

这样就得到了训练集：具有m个样本（可能重复）的数据集$D^{\prime}$，和测试集：未出现在$D^{\prime}$中的样本集合$D-D^{\prime}$。

Q：某个样本在m次操作中没有被选中的概率是多少？

A：

即每个样本都有36.8%的概率不被选为训练数据，那么根据数学期望可得训练集的大小，即$E(D-D^{\prime})=0.368*\left\vert D\right\vert$

使用这样的测试集完成的估计，也称作“包外估计”（out-of-bag estimation）

注意：

  • 改变了数据分布

所以，当数据分布不那么重要，或数据集过小时，可以考虑自助法。

调参与验证集

算法的参数：一般由人工设定，亦称“超参数”，数目常在10以内。

模型的参数：一般由学习确定，数目可能极多，深度学习中可达上百亿。

对算法的参数进行调整，即“参数调节”，简称“调参”（parameter tuning）。

事实上，前文中提到的，从训练集中划分出的、用于评估模型的数据，常称为“验证集”（validation set）。而真正的测试集是指在实际使用中遇到的、真的没有标签的数据。

当通过评估确定算法的参数后，因评估过程中仅使用训练集训练模型，所以应该用这些确定的参数对全部数据（训练集+验证集，即D）重新训练出模型，提交给用户。

性能度量

性能度量（performance measure）：对学习器的泛化性能进行评估。

错误率、精度

回归任务中：

均方误差（mean squared error）：

给定数据分布$\mathcal{D}$和概率密度函数$p(\cdot)$的一般形式：

分类任务中：

错误率：

正确率：

给定数据分布$\mathcal{D}$和概率密度函数$p(\cdot)$的一般形式：

查准率、查全率

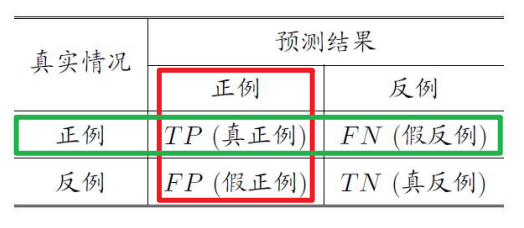
分类结果混淆矩阵

TF：预测对了或错了

PN：预测结果

例如FN（假反例）：预测错了，给预测成反例了。

查准率（precision）：预测结果准确的比率，如“预测出的真的好瓜（$TP$）占预测出的好瓜（$TP+FP$）的多少”

查全率（recall）：预测结果全面的比率，如“预测出的真的好瓜（$TP$）占所有好瓜（$TP+FN$）的多少”

$F1$、$F_\beta$

为了同时考虑查准率与查全率，同时又不忽视较小值，我们可以对二者进行调和平均，得到F1度量。

即

如果对P和R有偏好，可以对二者进行加权调和平均，得到$F_\beta$度量。

注. 这里的权重$\beta$加在R上，P的权重为1。所以当$\beta < 1$时，P更重要；当$\beta > 1$时，R更重要。

比较检验

学习器间的性能比较是一件复杂的事情，因为：

  • 测试性能不等于泛化性能（验证集不等于测试集）
  • 测试性能随测试集变化
  • 很多机器学习算法本身有一定的随机性

我们可以使用统计假设检验（hypothesis test）在统计意义上比较学习器的泛化性能。

单个学习器假设检验：二项检验（binomial test）、t检验（t-test）

两个学习器假设检验：交叉验证t检验、McNemar检验

多个学习器假设检验：Friedman检验、Nemenyi后续检验

测试

题14

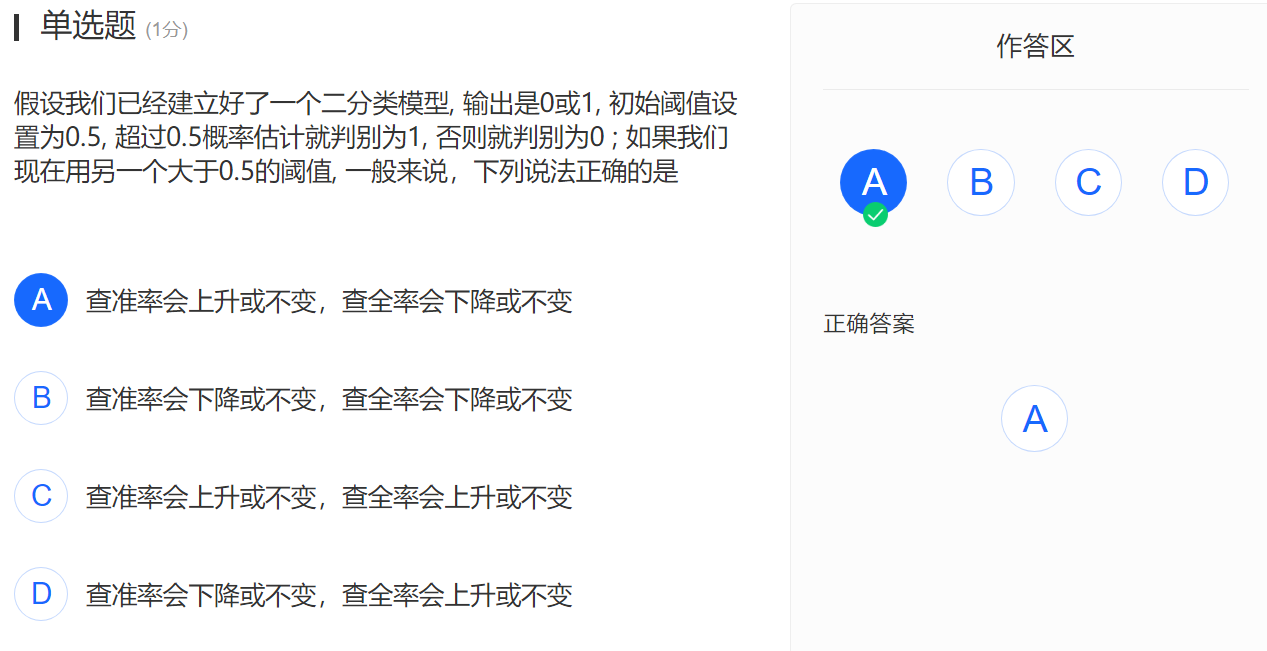
阈值上升，则预测为正类的样本（P）可能变少，预测为负类的样本（N）可能变多。因R的分子含TP，可能变小，分母恒为真实情况正例数，所以R下降或不变。根据P-R曲线（这不是个经验曲线吗？一定准确？），P上升。

线性模型

人类很难直接思考非线性问题，而在思考线性问题时可以有几何上的直观印象，基于这种直观印象，再加上一些技巧，便可能得到复杂的非线性问题的解决方案，所以线性模型很重要。

回归（regression）：该词源于生物学，意思是平均而言，子代的表现型比其父代更接近该物种的基因型应该表现出来的样子。所以回归就是根据样本的“表现型”确定其“基因型”。在统计学上，指确定变量之间的关系。

线性回归

线性回归（linear regression）：将变量间的关系建模为线性方程（线性模型）的回归分析。

线性回归在分类问题中，建模出一个线性方程，用于将不同样本“分开”。

线性回归在回归问题中，建模出一个线性方程，用于将样本“串起来”。

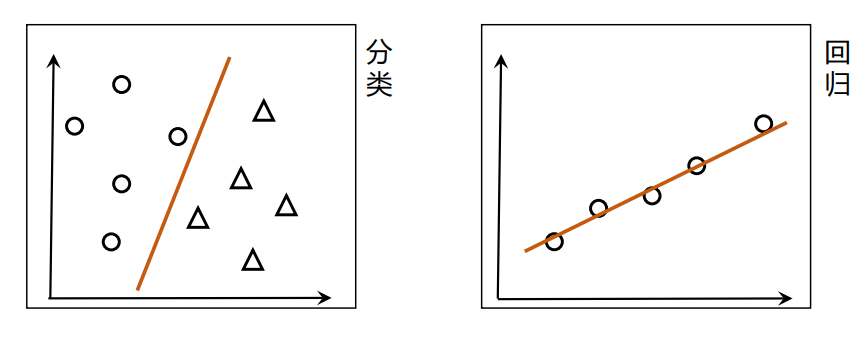
以上图为例，即确定

注. $\simeq$是\simeq，“similar equal”，近似相等。

更一般地，该线性模型的标量形式为：

向量形式为：

Q：若某一组输入的属性是离散的，如三值长度属性：{“长”，“中”，“短”}或三值敲声属性：{“浊响”，“清脆”，“沉闷”}，如何回归分析？

A：可以对输入属性进行处理，若属性值间存在“序”（order）关系，则可将其连续化，成为连续值，如长度属性可转化为$\{1.0, 0.5, 0.0\}$。若属性值间不存在序关系，则可以将其one-hot编码，成为one-hot向量，如敲声属性可转化为$\{(1, 0, 0), (0, 1, 0), (0, 0, 1)\}$

注. pandas中通过get_dummies（转哑变量）实现one-hot编码。

Q：线性回归怎么得到线性模型的呢？

A：通过使均方误差最小化，解出$w^$和$b^$

注.

$\left(x_1, x_2, …, x_n\right)$代表行向量

$\left(x_1; x_2; …; x_n\right)$代表列向量

线性回归求解析解（最小二乘解）

上述通过使均方误差最小化得到的解，也叫最小二乘/最小平方（least square method）解。

最小二乘解是一种解析解/闭式解（Closed-form expression），其解法如下：

分别对$w$和$b$求导

令导数为 0, 得到解析解:

因为是一个关于$w$和$b$的凸函数，所以其关于$w$和$b$的导数为0时，解得的就是最优解，对应全局极小点。

推导过程：

多元线性回归

如第一节中所述，线性回归的一般形式是

其中$\boldsymbol{x_i}=\left(x_{i1}; x_{i2}; …; x_{id}\right)$，样本共有$d$个属性。

这便是“多元线性回归”（multivariate linear regression）。

类似地，我们仍可以利用最小二乘法得到其最优参数。但为了方便解，我们首先对一般形式进行调整。

令

即

那么，数据集即为

类似地，令均方误差最小

注. 需要从一般形式推导至向量形式

设

对$\hat{\boldsymbol{w}} $求导，得

令其为零即可得$\hat{\boldsymbol{w}}$

但，若想解出$\hat{\boldsymbol{w}}$，需要对$\mathbf{X}$求逆！

所以，若：

  • $\mathbf{X}^{\mathrm{T}}\mathbf{X}$为满秩矩阵或正定矩阵，则可以解得唯一$\hat{\boldsymbol{w}}^* = \left(\mathbf{X}^{\mathrm{T}}\mathbf{X}\right)^{-1}\mathbf{X}^{\mathrm{T}}\boldsymbol{y}$
  • $\mathbf{X}^{\mathrm{T}}\mathbf{X}$不为满秩矩阵，则$\hat{\boldsymbol{w}}$不唯一，此时需要引入归纳偏好/正则化使其可解

广义线性模型

在$f(\boldsymbol{x})$预测出$y$后，我们还可以预测$y$的“衍生物”（以$y$为自变量的其他函数），即

其中$g(\cdot)$称为“联系函数”（link function），其单调可微、连续且充分光滑。

其等价于

即我们用线性模型，逼近/预测了标记的“衍生物”，这样得到的模型称为“广义线性模型”（generalized linear model）。

当$g(\cdot) = ln(\cdot)$时，即得到“对数线性模型”（log-linear model）

首先预处理标记，然后以线性回归求解线性模型的参数，最后得到标记真实的模型——指数模型。

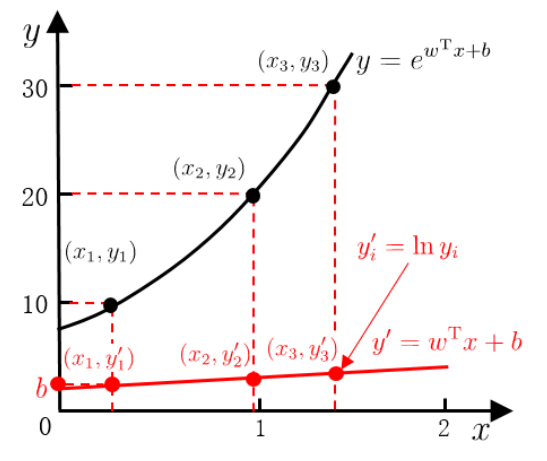
注. 广义线性模型的参数估计常通过加权最小二乘法或极大似然法进行。

对数几率回归

使用线性模型和广义线性模型进行回归分析，可以解决回归任务。

那么对于分类任务，事实上是在更进一步地，将线性模型的连续预测值$z$映射到离散的真实标记$y$。

以二分类任务为例，设其输出标记 $y \in \{0, 1\} $，其线性回归模型及其预测值$z=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b$。

那么为了将$z$映射到$y$，有一个最理想的函数“单位阶跃函数”（unit-step function）

其在预测值大于零时判为正例，小于零时判为负例，等于零（临界值）时任意判别，取两标记0和1的平均值0.5。

但单位阶跃函数性质很差，不连续且不可微，所以需要寻找能在一定程度上近似它的、性质好的“替代函数”（surrogate function）。

我们常用“对数几率函数”（logistic function）替代单位阶跃函数，其表达式为：

二者的函数图像为

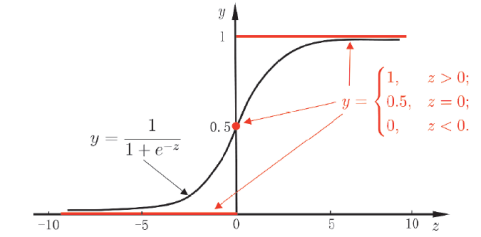
对数几率（对率）函数是一种代表性的Sigmoid函数（形似“S”的函数），其单调可微、任意阶可导，并且能将$z$映射到接近0或1的$y$，且在$z=0$附近很“陡”。

注. “对数几率”logistic一词源自统计学造词术语logit，其原本的单词为log odds，odds是“事件发生的概率与事件不发生的概率之比”，可译作“几率”或“发生比”。

将线性模型代入对数几率函数（将对率函数视作$y=g^{-1}(\cdot)$），得到广义线性模型$y=g^{-1}(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b)$

将其转化为线性回归的形式，即

$y$是学习器将样本视作正例的可能性，$1-y$是学习器将样本视作负例的可能性，所以$\frac{y}{1-y}$便是odds，$\ln\frac{y}{1-y}$便是log odds，即logit。所以该模型称作“对数几率模型”。

虽然对数几率模型是用线性回归方法确定的，也被叫做对数几率回归（logistic regression），但其实际上用于分类任务。

注. 统计回归方法只用于确定一个模型，模型适用于分类任务还是回归任务，是由模型自身决定的。

优点：

  • 无需事先假设数据分布（直接对原始的“类别”可能性建模，即将$\mathbb{R}$压缩到(0, 1)）
  • 可得到“类别”的近似概率预测
  • 可直接应用现有数值优化方法求取最优解（模型/目标函数的对数似然函数是任意阶可导的凸函数）

对数几率回归求近似解

Note. $P(A\mid B)$, is usually read as “the conditional probability of A given B“.

事实上， $y = \frac{1}{1 + \exp{\left(-\left(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}+b\right)\right)}}$ 是非凸的，所以不能用最小二乘法确定模型。

既然原函数是非凸的，我们可以考虑其“对数似然函数”（log-likelihood function）。

似然，是指当已知结果时，对其参数的推测。（也很类似从“表现型”得到“基因型”）

例如在二分类问题中，似然函数就是

当其最大时所对应的参数就最接近原函数的解。

在计算机处理较小数的乘法时可能会发生数值下溢，所以使用对数似然，即对似然函数取对数。

当线性模型参数$\boldsymbol{w}$和$b$确定时，可得$y$的后验概率估计$p(y_i \mid \boldsymbol{x})$

解得

现在确定线性模型参数$\boldsymbol{w}$和$b$（将它们设为$\boldsymbol{\beta}$），令

即

注. 设为$\boldsymbol{\beta}$是因为最优化中二阶导方法喜欢用这个符号。

令

那么，每个似然项表达式为

对数似然函数为

用最优化形式表达最大似然法

化简似然项$p(y_i \mid \hat{\boldsymbol{x}}_i; \boldsymbol{\beta})$

即

注. 我觉得这里我的化简方法比西瓜书和南瓜书更简单。

其对数似然

$$ \begin{aligned} \ln p(y_i \mid \hat{\boldsymbol{x}}_i; \boldsymbol{\beta}) &= {y_i}{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i}-\ln\left({1 + \exp\left(\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i\right)}\right)\\ &= \ln \exp \left({y_i}{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i}\right) - \ln\left({1 + \exp\left(\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i\right)}\right)\\ &= \ln \frac{{y_i}{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i}}{{1 + \exp\left(\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i\right)}} \end{aligned} $$

最大似然法的最大化式等价于

即

$$ \min \quad \sum_{i=1}^{m}\ln \frac{{1 + \exp\left(\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i\right)}}{{y_i}{\boldsymbol{\beta}^{\mathrm{T}} \hat{\boldsymbol{x}}_i}} $$

是一种无约束优化问题。

此时的求和项，是一个关于$\boldsymbol{\beta}$高阶可导的、连续的凸函数，证明先贴南瓜书，等我啃完西瓜书再回来重写。

所以我们可以采用梯度下降法、牛顿法等二阶导最优化方法求得其近似最优解$\boldsymbol{\beta}^*$

若使用牛顿法，其第$t+1$轮迭代解的更新公式为

其中，关于$\boldsymbol{\beta}$的一阶、二阶导数分别为

但我们还是偏向使用梯度下降法解决问题。

Q：为什么是近似最优解？

A：梯度下降法和牛顿法，二者的迭代终止条件均为$\left|f\left(\boldsymbol{x}^{t+1}\right)-f\left(\boldsymbol{x}^t\right)\right|<\epsilon$，且牛顿法的迭代公式通过必要条件推导而来，不保证是极小值点。

Q：为什么更偏向使用梯度下降法？

A：因为梯度下降法的更新公式$w = w + \Delta w$是迭代的，更适合计算机采用并行处理，速度快。牛顿法每次迭代时需要求解Hessian矩阵的逆矩阵，计算量通常较大，速度慢。

Q：为什么不用一阶导方法了？

A：当输入是向量时，需要涉及到矩阵的逆矩阵（对应标量计算中的除法），如多元线性回归中的最优解$\hat{\boldsymbol{w}}^* = \left(\mathbf{X}^{\mathrm{T}}\mathbf{X}\right)^{-1}\mathbf{X}^{\mathrm{T}}\boldsymbol{y}$，而输入矩阵很可能不存在逆矩阵。

类别不平衡

类别不平衡（class-imbalance）：分类任务中不同类别的样例数目差别很大的情况。

以二分类问题为例，通常的分类思想是，线性模型预测出的$y$（或者说$\hat{y}$）大于某个阈值（threshold）时，将其判为正例，最朴素的阈值是0.5，即

或用odds表示

假如样本中正例过少，而正例又很重要时（不能预测错了），那么我们必须要解决类别不平衡问题。

设$m^+$表示训练集中的正例数目，$m^-$表示训练集中的负例数目。

那么，一种自然的想法就是按照比例降低阈值，提高将样本判断为正例的可能性

即

那么，即可设$y^{\prime}$，使其满足

这就是解决类别不平衡的一个基本策略——“再缩放”/“再平衡”（rescaling/rebalance）。

但因为训练集和真实情况的分布往往不同（即不是“无偏采样”），训练集中正例少，不一定说明gt正例少，所以不一定准确。

实际上，现在针对类别不平衡实现的做法有：

  • 欠采样/下采样（undersampling/downsampling）：去除一些反例，使正、反例数目接近。如EasyEnsemble算法（划分反例、集成）
  • 过采样/上采样（oversampling/upsampling）：增加一些正例，使正、反例数目接近。如SMOTE算法（插值）
  • 阈值移动（threshold-moving）：使用原始训练集训练，预测时使用$y^{\prime}$进行决策。

测试

这一章的测试开始有计算了。

题6

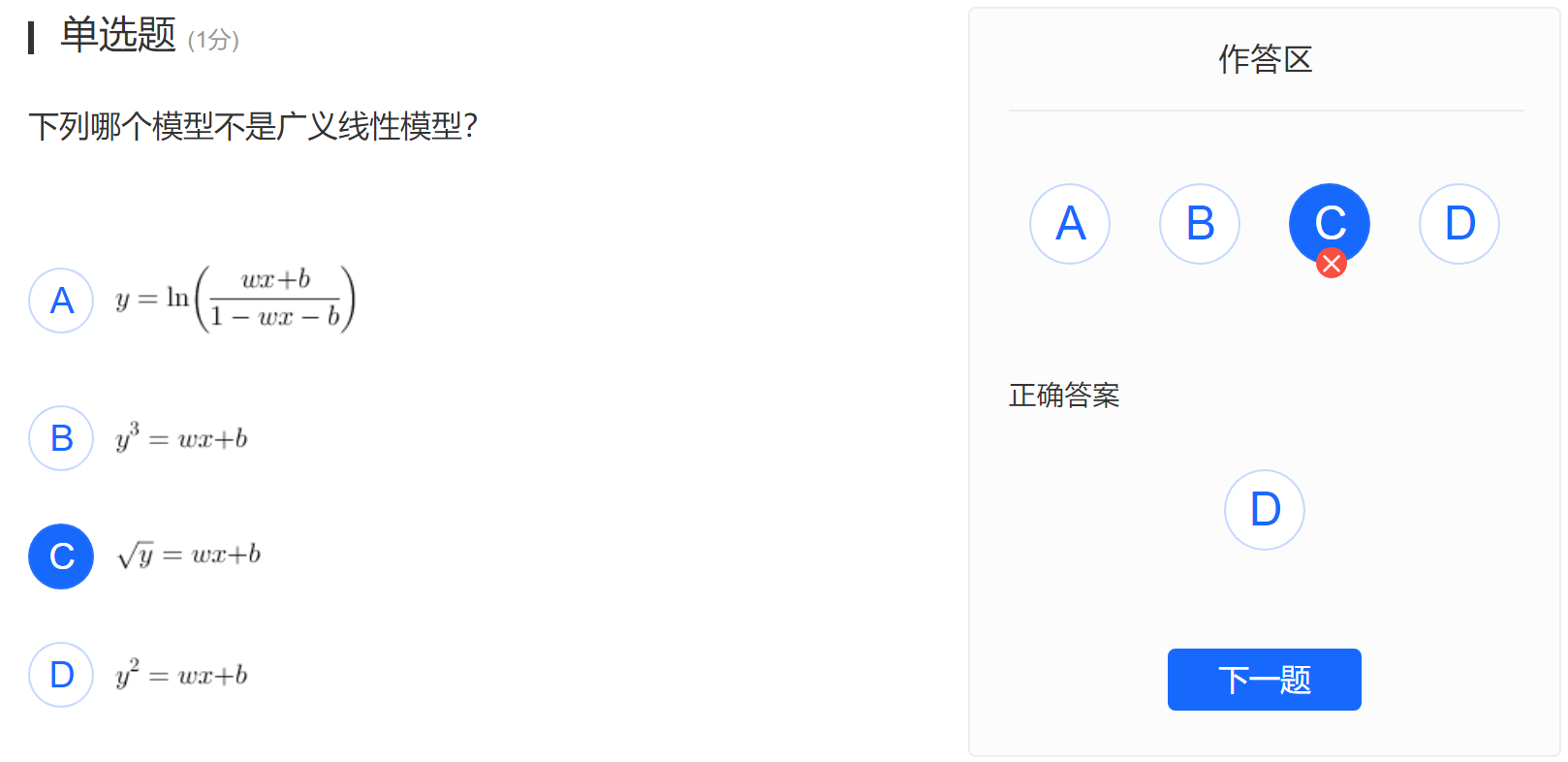
A经化简，为$g(y) = \frac{e^y}{1 +e^y} = \boldsymbol{w}^\mathrm{T} \boldsymbol{x} + b$，与B、C同样为单调函数；而D是非单调函数。

因$g(\cdot)$是单调、可微、连续、充分光滑的，所以答案是D。

题7

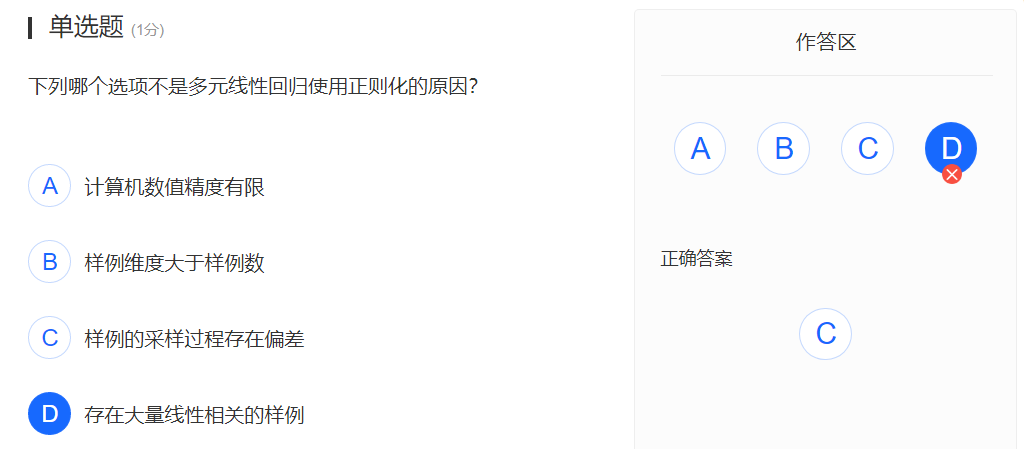
多元线性回归使用正则化的原因：

  • 计算机数值精度有限
  • 样例维度大于样例数
  • 存在大量线性相关的样例

注. 不明白为什么，我只知道正则化可以防止过拟合。

题9

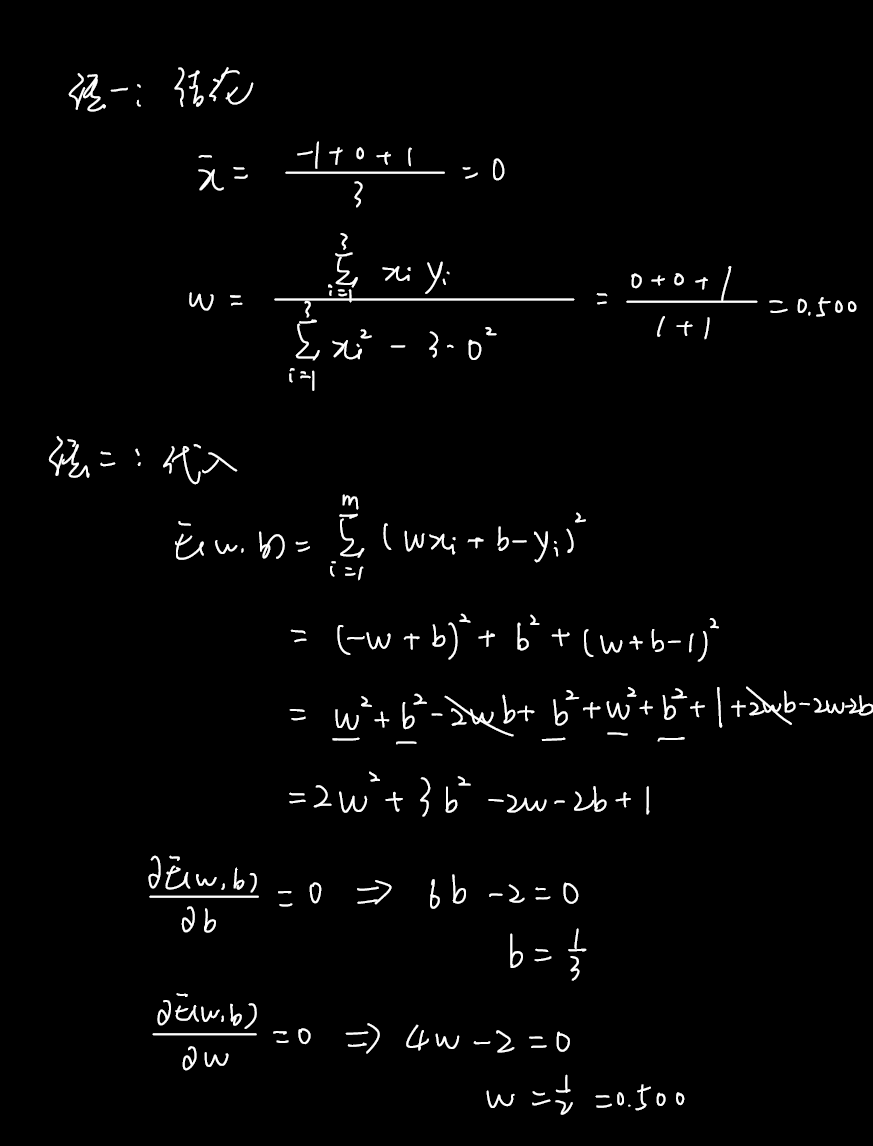
题10

这个损失函数带着$\sum$推导很难受，只是为了做题的话可以直接代入。

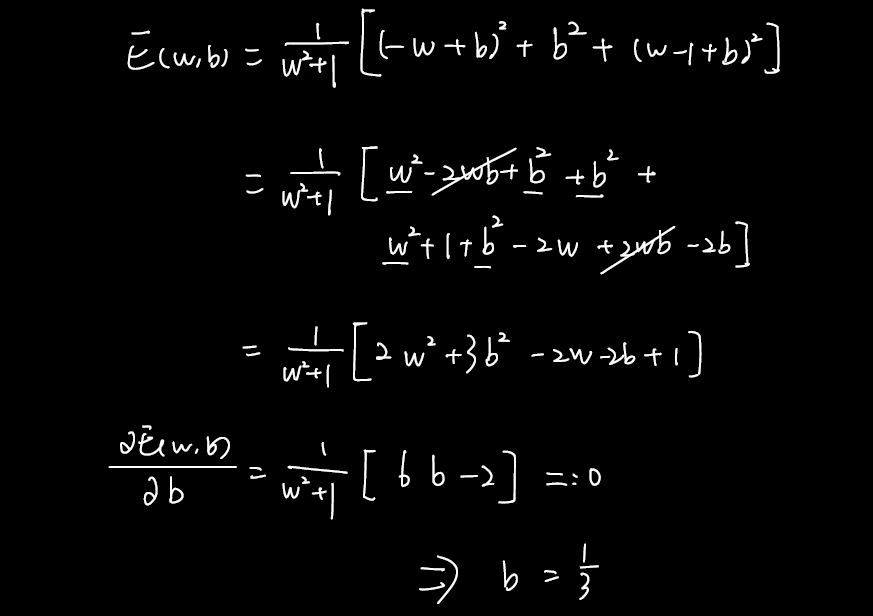
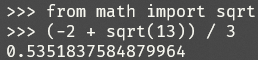
Q：为啥答案里没有负的那个？

A：也许负的那个不是最小值点。

题12

OvR，One vs. Rest，一对其余。

类别均衡的10分类问题，所以正反例的样本数目之比为$m^+:m^- = 1:9$，$y > \frac{m^+}{m^+ + m^-} = \frac{1}{10} = 0.100$。

决策树

决策树基本流程

决策树（decision tree）是一种特殊的树，其包含：

  • 一个根结点
  • 若干个内部结点（非根/叶结点）
  • 若干个叶结点

其中，每个结点都包含“样本集合”。根节点对应“样本全集”，内部结点对应“属性测试的结果”，叶结点对应“决策结果”。从根结点到叶结点的路径对应“判定测试序列”。

决策树学习，目的是生成一棵泛化能力强的决策树，其算法遵循简单直观的“分而治之”（divide-and-conquer, 分治）策略：

自根至叶递归

在每个内部结点寻找一个“划分”（split or test）属性

三种停止条件：

  • 当前结点包含的样本均属于同一类别，无需划分
  • 当前属性集为空, 或是所有样本在所有属性上取值相同，无法划分
  • 当前结点包含的样本集合为空，无法划分

算法描述：

（关于情形3，直接返回了的话，后面的属性值怎么办？）

信息增益属性划分准则

许多机器学习算法都受到了信息论的启发，决策树也不例外。

按上一节中的决策树学习策略，我们可以看出，随着划分过程的不断进行，算法希望分支结点所包含的样本尽可能属于同一类别，即结点的“纯度”（purity）越来越高。

“纯度”越高，“不确定度”就越低，所以我们可以用描述不确定度的“信息熵”来作为纯度指标。

信息熵（information entropy）：描述信息源$X$中各可能事件$x$发生的不确定性。是随机变量$X$的自信息$-\log\ p(⁡x)$（概率越大，信息量/不确定度越小）的数学期望。

若样本集合$D$中第$k$类样本所占的比例为$p_k(k = 1, 2, \ldots, |\mathcal{Y}|)$，则$D$的信息熵定义为

即$\operatorname{Ent}(D)$越小，$D$的纯度越高。

当$D$中只有一类样本时，$\operatorname{Ent}(D)$最小，，

当$D$中的样本类别均衡（均分）时，$\operatorname{Ent}(D)$最大，，

注. \operatorname就是切换成直立体，和\log类似。

接下来再来看第8步

训练集 ;
属性集 .

8: 从$A$中选择最优划分属性$a_*$;

对于属性$a_i$，假设其有$V$个属性值。

那么，使用属性$a_i$划分时会产生$V$个分支结点。其中，第$v$个分支结点包含$D$中的、在属性$a_i$上取值为$a_i^v$的样本，记为$D^v$。则使用属性$a_i$划分$D$所获得的“信息增益”（information gain）定义为

其中$\frac{|D^v|}{|D|}$为分支结点的权重，样本数越多的分支结点，影响越大。

$\operatorname{Ent}(D)$是划分前的信息熵，$\sum\limits_{v=1}^{V}\frac{|D^v|}{|D|}\operatorname{Ent}(D^v)$是划分后的总信息熵，划分前后的信息熵下降得越大（“纯度提升”越大），所获得的信息增益就越高。

所以，我们可以用信息增益的大小来选择$a_*$

注. ID3算法中使用信息增益作为划分准则。

下面以西瓜数据集2.0为例进行划分。

该数据集包含17个训练样例，欲训练出一颗决策树，用来判断没切开的瓜是不是好瓜。

首先可以看出，$\mathcal{Y} = \{是， 否\}$，$|\mathcal{Y}|=2$。

其中，正例所占比例为$p_1= \frac{8}{17}$，反例所占比例为$p_2=\frac{9}{17}$。

那么，根节点的信息熵为

当前属性集合$A = \{色泽, 根蒂, 敲声, 纹理, 脐部, 触感\}$，现在计算按每个属性划分$D$所带来的的信息增益。

首先是属性“色泽”，其属性值为$\{青绿, 乌黑, 浅白\}$，分别对$D$进行划分，有

划分后，3个分支节点的信息熵分别为

计算按“色泽”划分$D$所带来的信息增益

同理，计算按其他属性划分$D$所带来的信息增益

因此，最优划分属性为“纹理”，按其划分$D$所形成的一层决策树为

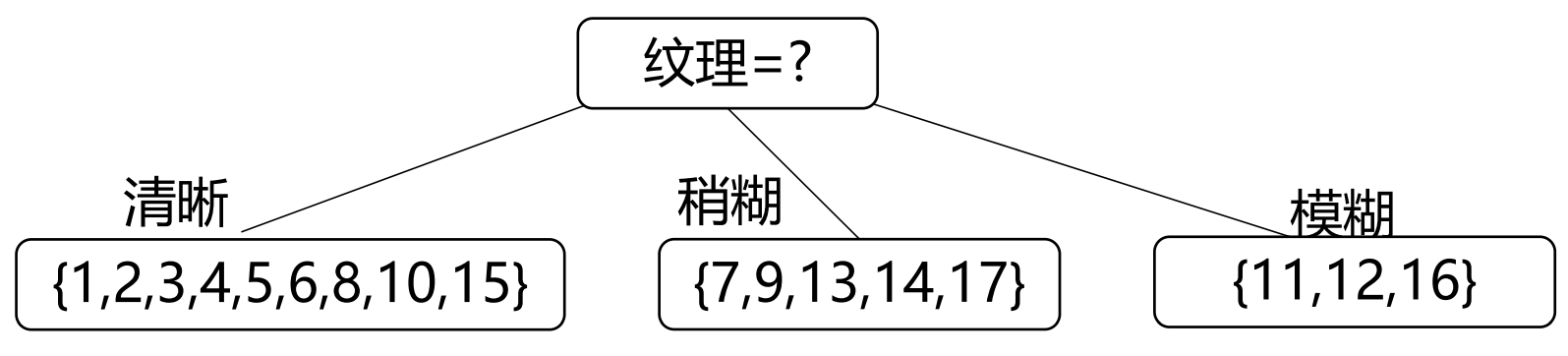
继续递归划分，进入第一个分支结点（“纹理=清晰”）。

该结点所包含的样例集合$D^1=\{1, 2, 3, 4, 5, 6, 8, 10, 15\}$，属性集合$A = \{色泽, 根蒂, 敲声, 脐部, 触感\}$，计算按每个属性划分$D^1$所带来的的信息增益。

按“根蒂”、“脐部”、“触感”划分$D^1$均得到了最大的信息增益，因此应根据归纳偏好（随机也属于一种归纳偏好）选择其中之一作为$D^1$的划分属性。

继续递归，直到算法结束，得到训练好的决策树。

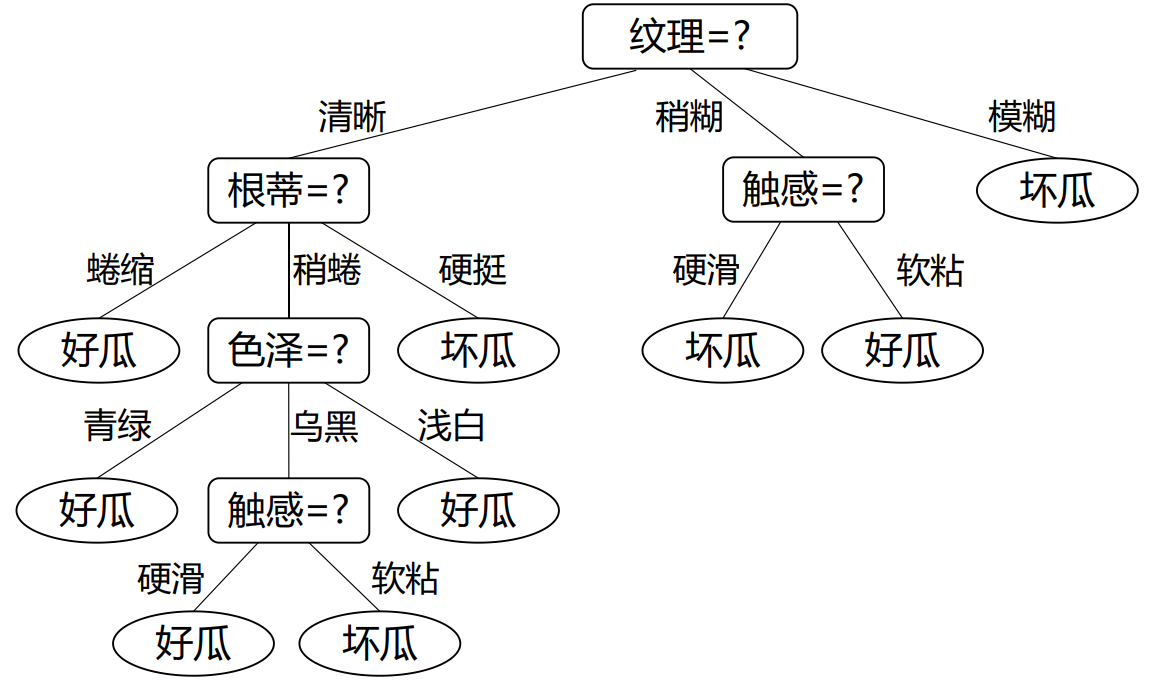
其他属性划分准则

事实上，信息增益$\operatorname{Gain}$划分准则有其归纳偏好：偏好按属性值多的属性划分。

例如，按属性“编号”（“编号”是训练集中属性值最多的属性）划分$D$，所产生的分支结点们的“加权信息熵”为0，即，纯度最大，所获得的信息增益最大。但按“编号”划分，所产生的这棵“纯度最高的”决策树不具有泛化能力。因为“编号”与“好瓜”没有相关性，不能说前8个采集的西瓜一定是好瓜，9~17个采集的西瓜一定不是好瓜，后面采集的西瓜不知道是不是好瓜，这是荒谬的。

增益率

Quinlan在他的决策树生成算法C4.5中使用了“增益率”（gain ratio）作为纯度指标，其定义为

其中，

称为属性$a_i$的“固有值”（intrinsic value）。

Q：为什么定义固有值为这种形式呢？

A（猜想）：首先，属性值越多，每个属性值的样本越少，其的权重$\frac{|D^v|}{|D|}$越小。令作为分母，作者希望属性值越少（权重越大），$\operatorname{IV}$越小，增益率越大，需要乘一个与权重成反比的函数。又因为权重，所以引入负对数函数（如图），形成。

但事实上，$-x\log_2x$不是单调递减的，而是先增后减。

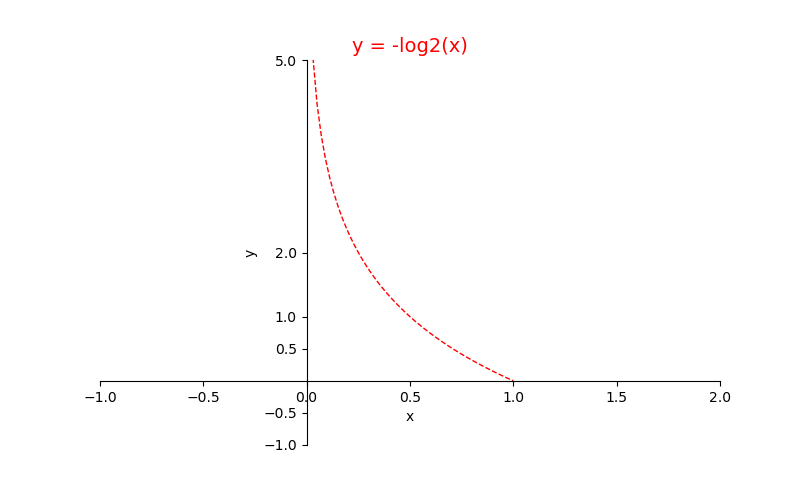
那么现在我们知道，划分准则的归纳偏好：偏好按属性值少的属性划分。

所以C4.5生成算法加入了启发式：先用$\operatorname{Gain}$划分准则找出$\operatorname{Gain}$高于平均水平的属性，接着再用划分准则选择最高的。即希望从更纯净的划分属性中找属性值少的划分属性。

基尼指数

Quinlan在他的决策树生成算法CART（Classification and Regression Tree）中使用了“基尼指数”/“基尼不纯度”（Gini index/Gini Impurity）作为纯度指标，其定义为

其中，

$\operatorname{Gini}(D)$的意义为：可理解为“非同类率”。从D中无放回地、选取所有两类样本的组合，如果这些组合乘积的和越小，那么越纯净。或者说从$D$中无放回地（超几何分布，抽出后概率不变）选取到两个同类样本的概率（“同类率”）越大，那么越纯净。

基尼系数的第二种形式，源于以$e$为底的信息熵，对其中的$-\ln p_i$在$p_i = 1$处进行泰勒展开、取高阶项，即可得到$(1-p_i)$。所以，基尼不纯度实际上是信息熵的一个近似值。

使用带Peano余项的泰勒公式

得

$\operatorname{Gini_index}(D, a_i)$越低，即“非同类率”越低，“同类率”越高，划分所得的样本集合越纯净。

以基尼指数为属性划分准则，所选取的最优属性$a_*$为

事实上，研究表明：各种属性划分准则，虽然对决策树的尺寸有较大影响，但对泛化性能的影响很有限。

决策树的剪枝

更影响决策树泛化性能的手段，是剪枝（pruning）。

事实上，剪枝是缓解决策树过拟合现象的主要手段。因为当决策树过深时，较深结点的样本集合很小，即决策树学习到了这些少数样本独有的分布，将其剪掉虽然减小了训练性能，但防止了过拟合现象（故意不学习这些特性，不使用这些属性进行划分）。

决策树剪枝的基本策略有两种：

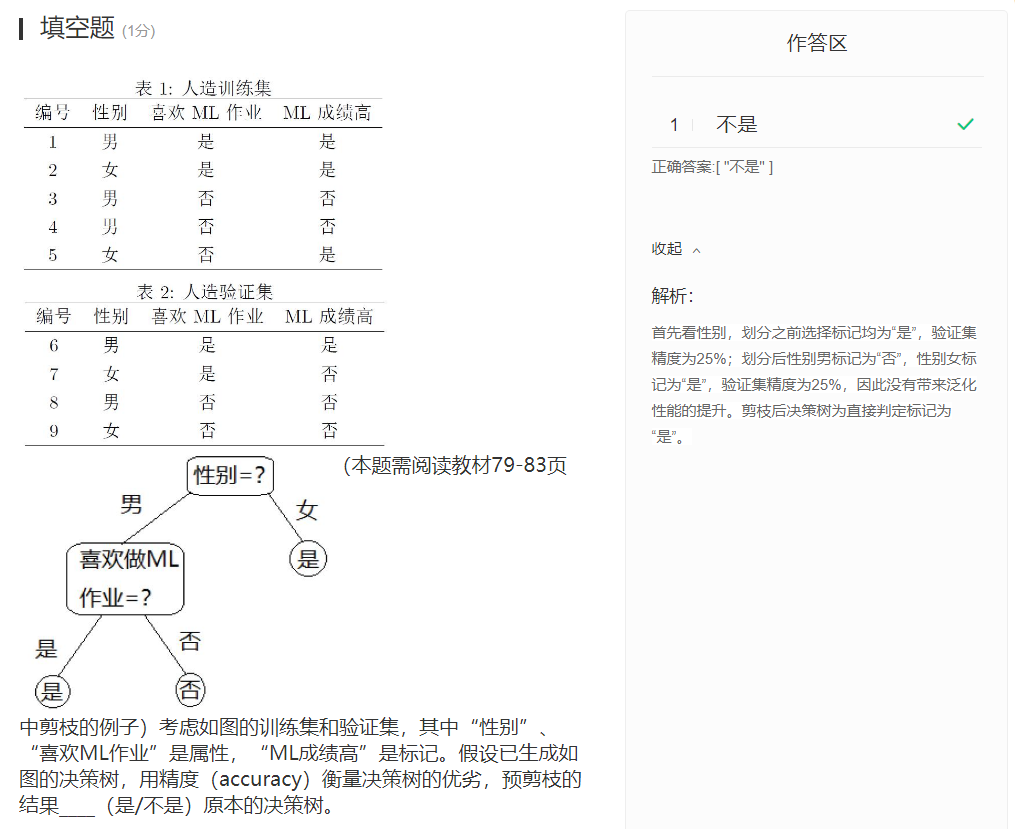
  • “预剪枝”（prepruning）：提前终止某些分支的生长，将其标记为叶节点。
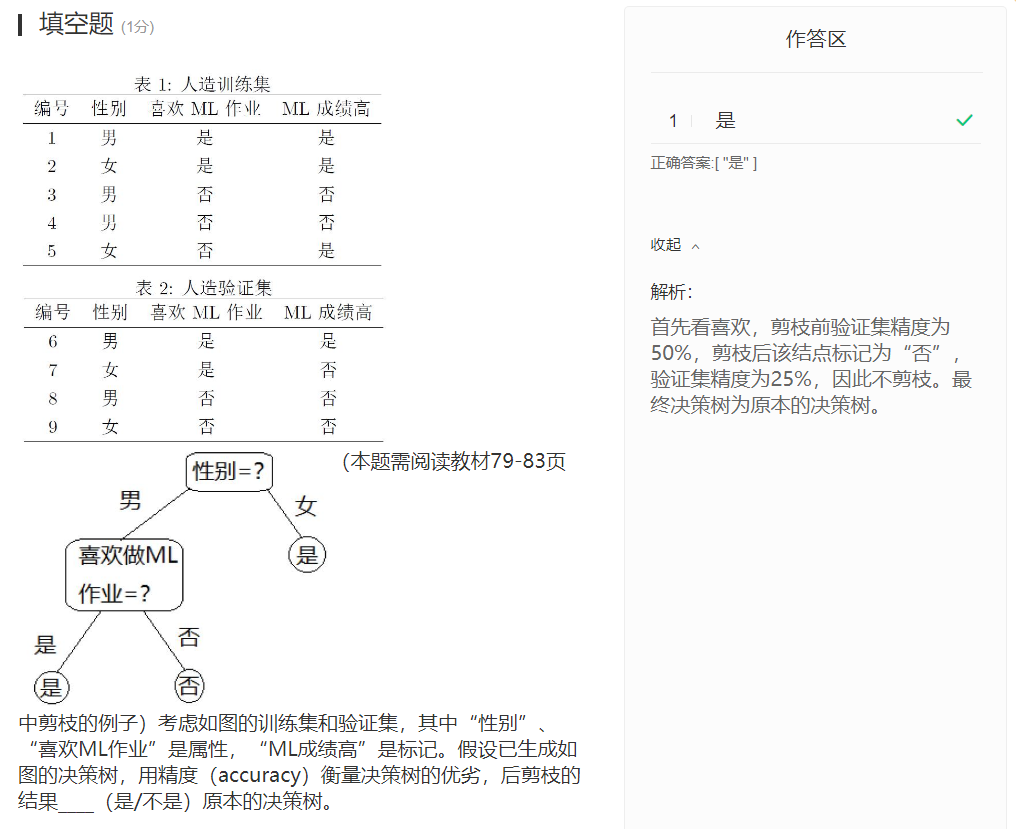
  • “后剪枝”（postpruning）：先生成一棵完整的决策树，再自底向上地将内部结点及其子树替换为叶节点。

只有在能带来泛化性能提升时，剪枝策略才将分支处理为叶节点。那么如何判断新树的泛化性能相对于原来的树有所提升呢？

这时就需要使用“模型评估与选择”中提到的评估方法去量化泛化性能。

缺失值的处理

现实任务中，样本通常是不完整的，即样本的某些属性值“缺失”（misssing）。

如果仅使用无缺失值（null）的样例，会造成极大的数据损失。

如果使用带缺失值的样例，需要解决两个问题：

  • Q1：如何确定划分属性？
  • Q2：确定划分属性后，若样本在该属性上为缺失值，如何划分该样本？

首先，每个样本$x$都需要有权重$w_x$，在学习算法开始时所有样本赋权为1。样本“摆烂”（被划分时属性值缺失）次数越多，其“后代”权重越小。

A1：使用属性$a_i$中无缺失值的样例计算按$a_i$划分$\tilde{D}$（$D$的无缺失子集）所获得的信息增益$\operatorname{Gain}(\tilde{D}, a_i)$，再通过其去估算按$a_i$划分$D$所获得的信息增益$\operatorname{Gain}(D, a_i)$。即

其中，

A2：将 划分所得的决策树 对 带缺失值样例 的后验概率当做先验概率。即“摆烂划分”：这个属性划分不出来就不在这划分了，按“样本权重”（预测结果的可能性）分配给下一层划分。

下面以西瓜数据集2.0$\alpha$为例进行带缺失值数据集的划分。

根节点无缺失子集$\tilde{D}$的信息熵

按属性“色泽”对无缺失子集$\tilde{D}$进行划分

划分后，在无缺失子集$\tilde{D}$上，3个分支节点的信息熵分别为

在无缺失子集$\tilde{D}$上，属性“色泽”的信息增益为

在带缺失训练集$D$上，属性“色泽”的信息增益为

同理，计算按其他属性划分带缺失训练集$D$所获得的信息增益

因此，最优划分属性为“纹理”，按其划分带缺失训练集$D$所形成的一层决策树为

测试

题7

对西瓜数据集2.0，属性“色泽”的基尼指数为____（保留2位有效数字）

正确答案:[ “0.43” ]

题10

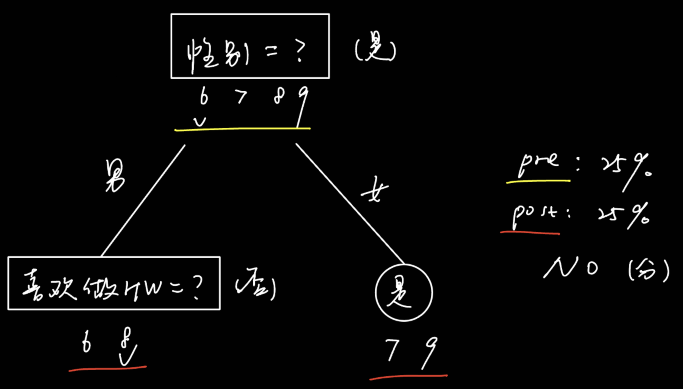
题11

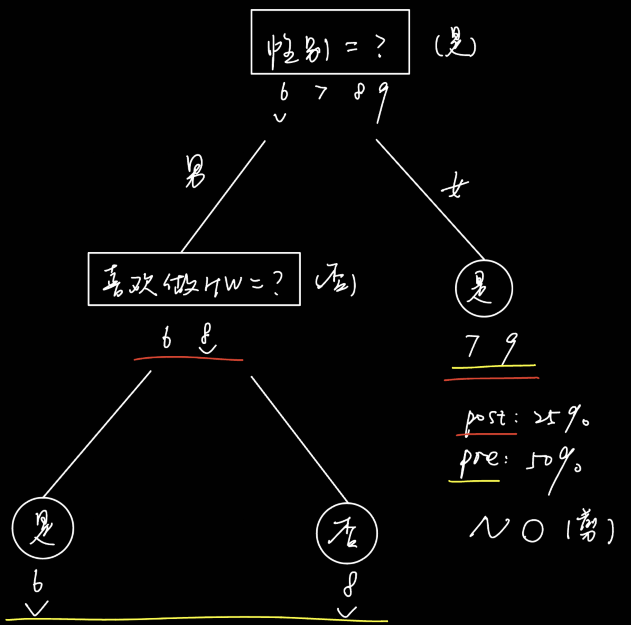
支持向量机

支持向量机基本型

在“线性模型”一章中，我们提到，对于“分类”问题，需要在样本空间确定一个超平面，用于将不同类别的样本“分开”。

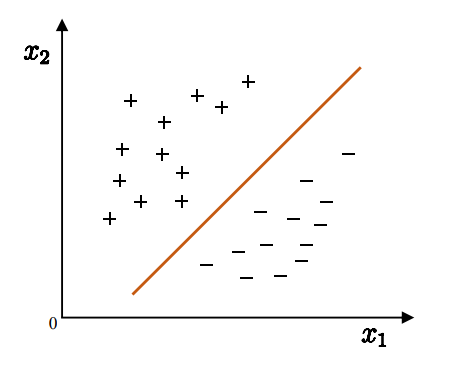
但，确定的超平面可以有很多，哪一个最好呢？

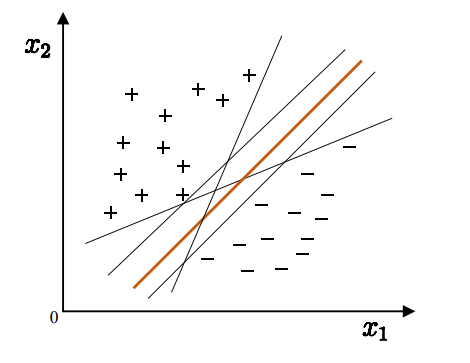
直觉上，正中间的超平面最好，因为它的鲁棒性最好，泛化能力最强。

使用支持向量机（Support Vector Machine, SVM）算法可以确定这个划分超平面，下面推导支持向量机算法中最优化问题的一些形式和它们的解。

首先，超平面方程的向量形式为

假设划分超平面存在，找到正例距超平面最近的样本，负例中距超平面最近的样本（下图中圈起来的样本）。可以发现，它们直接确定了超平面，我们称这些样本为“支持向量”（support vector）。

定义一个超平面，其经过正例支持向量，方程为

定义一个超平面，其经过负例支持向量，方程为

若同时缩放$\boldsymbol{w}\rightarrow k\boldsymbol{w}$和$b\rightarrow kb$，所有超平面的方程都会$*k$，但它们是等价的，所以可以定义经过支持向量的两类超平面距划分超平面的距离为$1$和$-1$。

样本空间中任意点$\boldsymbol{x}_i$到超平面$\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x} + b$的距离$r$为

由上述假设，可得两异类支持向量到划分超平面的距离之和，将其定义为间隔$\gamma$

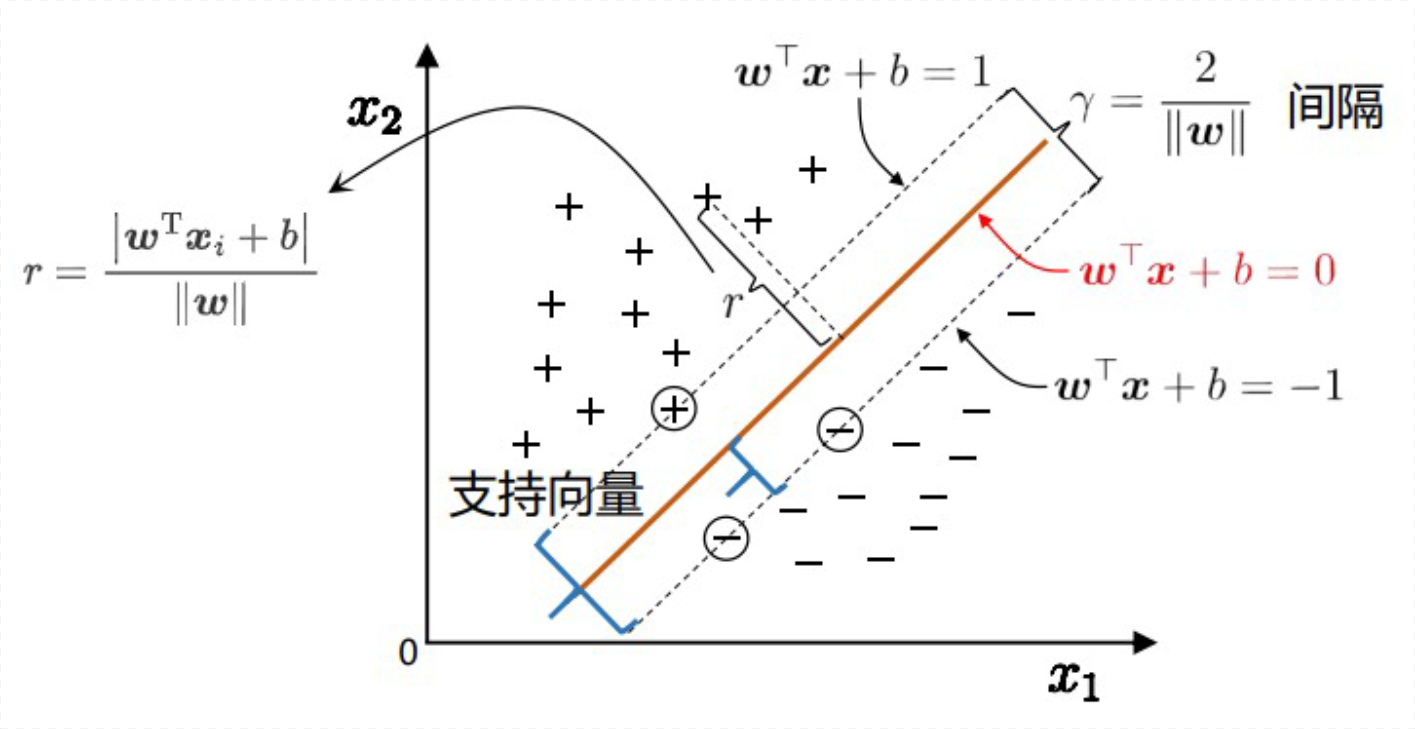
所以，确定划分超平面，即确定最大的间隔$\gamma$，使超平面正确划分所有样本。

使用最优化形式描述目标

其等价描述

这就是支持向量机的基本型，即样本在原始样本空间内线性可分，原始样本空间内找到划分超平面。支持向量机的基本型是一个凸二次规划问题，可以使用现有工具包求解。但在计算机领域，我们使用拉格朗日乘子法将基本型转换为它的对偶问题，因为它的对偶问题可以使用更高效的算法迭代求解，计算机可以并行处理。

对偶问题与解的特性

推导

拉格朗日乘子法（Lagrange multipliers）是一种优化方法，用于寻找多元函数在一组约束下的极值。

通过引入拉格朗日乘子，可将有$d$个变量与$k$个等式约束条件的最优化问题转化为具有$d+k$个变量的优化问题求解。

支持向量机基本型的原问题/主问题（primal problem）

对每条约束添加拉格朗日乘子$\mu_i \geq 0$，得到基本型的拉格朗日函数$L(\boldsymbol{w}, b, \boldsymbol{\mu})$

其中

当约束条件满足时，$L(\boldsymbol{w}, b, \boldsymbol{\mu}) <= f(\boldsymbol{w}, b) = \frac{1}{2}{|\boldsymbol{w}|}^2$，所以支持向量机的基本型等价于

这个$\min\text{-}\max$优化问题称为主问题的$\min\text{-}\max$形式。

Note. $\boldsymbol{\mu} \succeq 0$意为$\mu_i \geq 0, i = 1, 2, \ldots, m$。下面将$\min\text{-}\max$问题称作主问题，将$\min$问题称作原问题。

因主问题关于原变量的优化函数可能非凸，所以我们一般将其转化为关于拉格朗日乘子的凸函数。

令对$w$和$b$的偏导为0，可得

将其代回拉格朗日函数，有拉格朗日对偶函数$\Gamma(\mu)$

Note. 用到了很多次向量的乘法分配律。

$\underset{\boldsymbol{\mu}}{\max}\underset{\boldsymbol{w}, b}{\min} \ L(\boldsymbol{w}, b, \boldsymbol{\mu})$这个$\max\text{-}\min$问题，即为主问题$\underset{\boldsymbol{w}, b}{\min}\underset{\boldsymbol{\mu}}{\max} \ L(\boldsymbol{w}, b, \boldsymbol{\mu})$的对偶问题（dual problem），在约束条件下，其解与基本型（原问题）的解相同。

使用$\inf$表示$\min$，可得到对偶问题

对偶问题的优化函数是关于拉格朗日乘子的，所以一定是凸函数。

由上述推导可知，若想要对偶问题的解与主问题甚至原问题的解相同，则需要满足以下必要条件，即KKT条件。

KKT条件包括平稳条件（SVM有两个变量，所以有两个条件）、原问题可行性条件、对偶可行性条件、互补松弛条件等

支持向量机基本型的原问题是凸函数，所以KKT条件也是充分条件（强对偶性）。

通过互补松弛条件知，对于任意训练样本$(\boldsymbol{x}_i, y_i)$，总有$\mu_i = 0$或$y_i\left(\boldsymbol{w}^{\top} \boldsymbol{x}_i+b\right) = 1$，即如果样本不在约束边界上，那么$\mu_i = 0$，其约束失效，与$\boldsymbol{w}$无关；如果样本在约束边界上，那么$\mu_i \geq 0$，其约束生效，用于确定$\boldsymbol{w}$。

对于后者这些在约束边界上的样本，被称作支持向量（support vector）。

带着KKT条件解对偶问题（求解方法见下节），解得$\boldsymbol{\mu^*}$，其与原问题的解相对应，所以

通过

即可得到$\boldsymbol{w^*}$

任意选取一个支持向量$(\tilde{\boldsymbol{x}}, \tilde{y})$，通过

即可得到$b^*$

也可以选取所有支持向量，计算所有偏移项的均值

也可得到$b^*$

Note. 这里用的是邱锡鹏nndl书上的写法，西瓜书中将$y$作为分母也是一样的，反正支持向量的$y$的值为1或-1。

综上，得到支持向量机的划分超平面

那么，支持向量机的决策函数即为

总结

Note. 上述推导为了$\min\rightarrow\min \text{-}\max\rightarrow\max\text{-}\min$过程的可理解性，将其分为了三个问题，实际上只有两个问题，min-max问题是min问题的另一种形式。

原问题（基本型）

原问题的min-max形式

对偶问题

当满足KKT条件时，三者解相同，通过解对偶问题得到原问题的解。

Reference

最优化问题的KKT条件简要解释
拉格朗日乘子法及KKT条件

求解方法

对偶问题是一个凸优化问题，但同样地，因为前面多次提到过的原因，我们需要一种迭代解法。

SMO（Sequential Minimal Optimization）算法就是这样一种代表性算法。

为与原论文契合，此后使用$\alpha_i$代替$\mu_i$，$\alpha_j$代替$\mu_j$，$K(\boldsymbol{x}_i, \boldsymbol{x}_j)$代替$\boldsymbol{x}_i^T\boldsymbol{x}_j$。

重写的对偶函数为

其基本流程为

每轮重复以下两个步骤直至收敛：

  1. 选取一对需要更新的变量，设本轮为$\alpha_1$和$\alpha_2$
  2. 固定$\alpha_1$和$\alpha_2$以外的参数，求解对偶问题，更新$\alpha_1$和$\alpha_2$

在仅考虑$\alpha_1$和$\alpha_2$时，对偶函数成为

其中

由于对偶问题的KKT条件$\sum\limits_{i=1}^m \alpha_i y_i =0$，有

因为${y_j}^2 = 1$，所以可将$\alpha_2$用$\alpha_1$表示

接着对偶函数成为

此时的对偶函数已经成为了一个关于$\alpha_1$的凸二次函数，可以直接求导等于0得到构造解（闭式解）了。

那么如何选取两个变量使得性能更好呢？Platt提出了一种启发式方法。

Platt选择违反KKT条件的$\alpha_i$作为第一个变量，选择是对偶函数增长最快的$\alpha_j$作为第二个变量。

Reference

Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines

特征空间映射

前面几节讨论了支持向量机的基本型（样本在原始样本空间内线性可分）、其对偶问题、其对偶问题的解法。

那么如果样本在原始样本空间内非线性可分，不存在划分超平面，怎么划分样本呢？

我们可以将样本从原始样本空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

如“异或”的四个样本在二维特征空间内非线性可分，在三维特征空间内线性可分。

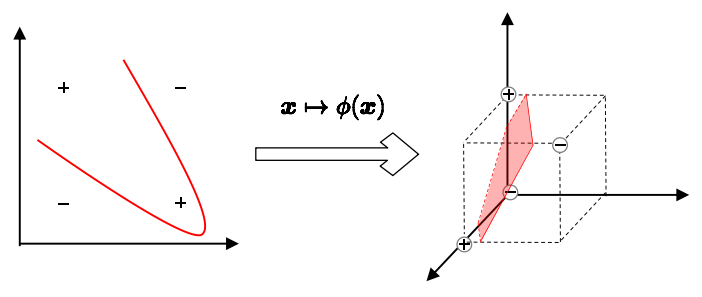
事实上，如果原始样本空间是有限维的，那么一定存在某些高维特征空间，使样本在其内线性可分。高维特征空间可能是无限维特征空间。

所以，只需找到合适映射$\phi(\cdot)$，将原样本空间中的所有样本映射到高维特征空间，然后在高维特征空间内解支持向量机的基本型，即可得到划分超平面的表达式。

映射（坐标变换、升维）

新样本空间内的划分超平面

新样本空间内的支持向量机基本型

新样本空间内的支持向量机基本型的对偶问题

求解后得到的划分超平面的函数表达式

可以发现，求解对偶问题得到$\boldsymbol{\mu}$时、根据$\mu_i$计算$f(\boldsymbol{x})$时，都需要计算两个 映射后的向量 的内积。

然而，由于映射后的向量维数可能很高、甚至可能是无限维，因此计算上是困难的。所以，我们需要另一个容易计算的，可以替代二者内积的函数。

核函数

设计这样一种函数$\kappa\left(\cdot, \cdot\right)$，输入原始样本空间中的低维向量$\boldsymbol{x}_i$和$\boldsymbol{x}_j$，即可得到它们经映射后得到的高维度向量的内积，即

我们称这种函数为核函数（kernel function）。

Note.

SMO算法中我们曾使用的记号即为核函数。

将$\phi(\cdot)$从n维线性空间映射得到的甚高维线性空间称作希尔伯特空间，记作$\mathcal{H}$。

希尔伯特空间是欧氏空间的一推广，即完备的内积空间（允许无穷维且不限于实数情形）。

引入核函数后，对偶问题可重写为

划分超平面的函数表达式可重写为

这种将表达式通过训练样本的核函数展开的形式，称为“支持向量展式”（support vector expansion）。

Q：什么样的函数可以作为一个核函数呢？

A：满足正定核函数充要条件或Mercer定理的函数可以作为一个核函数。

Mercer定理：若一个连续对称函数所对应的核矩阵半正定，则其就可以作为一个Mercer核函数。

正定核函数充要条件：若一个对称函数所对应的核矩阵半正定，则其就可以作为一个正定核函数。

正定核比Mercer核更具一般性（李航. 统计学习方法P122）

由定理或条件得到的核函数的等价定义。

Q：什么是核矩阵？

A：首先了解一下距离矩阵、Gram矩阵，再介绍核矩阵。

设数据集。

距离矩阵：样本间两两计算距离所排列成的矩阵。

$D$的距离矩阵为

其中，$d(\boldsymbol{x}_i, \boldsymbol{x}_j)$指两个样本之间的距离。该矩阵是一个对称矩阵，且主对角线元素为0。

Gram矩阵：样本间两两计算内积所排列成的矩阵

$D$的Gram矩阵为

该矩阵是半正定矩阵。

核矩阵：希尔伯特空间$\mathcal{H}$中的、$\kappa\left(\cdot, \cdot\right)$所对应的Gram矩阵。

$D$的核矩阵为

即

我猜的：核矩阵其实就是任意两样本间的测度/度量，所以extends自距离矩阵、Gram矩阵，所以核矩阵是对称、半正定矩阵。

因为对称是定义半正定的前提，所以半正定方阵在实数域一定是对称方阵，即半正定方阵一定是实对称方阵。因此在描述核函数时可以省略核矩阵的对称性。

$\phi(\cdot)$所映射的空间是$\mathcal{H}$

而$\kappa(\cdot, \cdot)$所隐式定义的空间被称作再生核希尔伯特空间（RKHS, Reproducing Kernel Hilbert Space）。

所以，选择合适的$\kappa$，找到其中的$\kappa^*$，其定义的$\operatorname{RHKS}$最接近$\mathcal{H}$，就是我们的目标。

注：半正定性是RKHS存在的必要条件，证明李航. 统计学习方法P118。

image-20221108194740952

支持向量机软间隔型

Note. 软间隔支持向量机部分被剪辑掉了，MOOC中并没有，这里简单介绍一下。

下图为软间隔支持向量机的基本思想：允许超平面划分错误一部分样本（红圈内的样本），这部分样本可以不计入优化目标中。

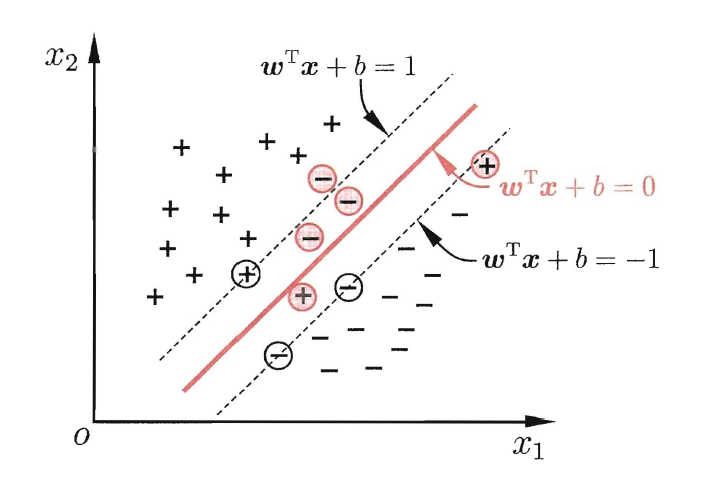
具体的实现方式是，为最优化目标施加惩罚项，成为

当样本被划分错误时，即$\ell_{0/1}$的参数小于0时，$\ell_{0/1}$的值为1。

那么，C即为该错误的“放大系数”，当C无穷大时，不允许超平面划分错误；当C为有限值时，允许超平面在一定程度上划分错误。

常见的损失函数：

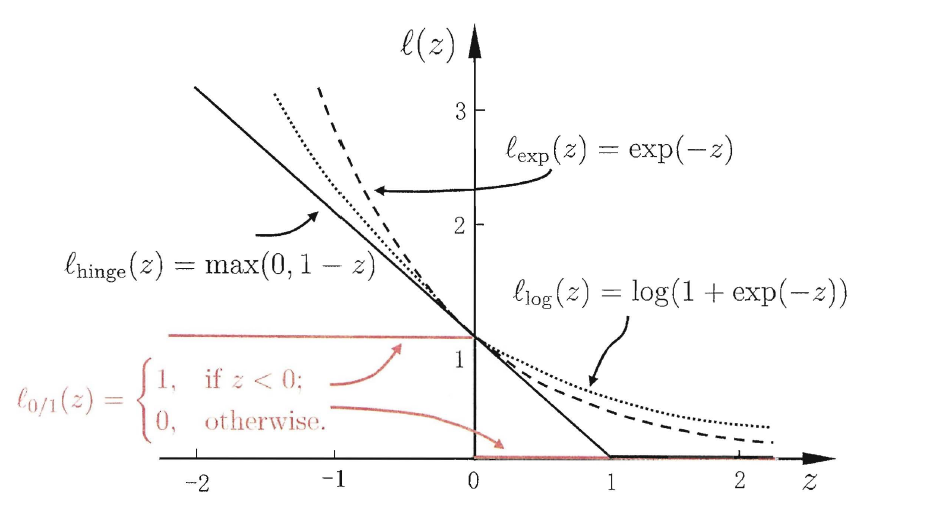
令这些损失的值为“松弛变量”（slack variables），记作$\xi_i$，则有

该优化问题即支持向量机软间隔型的主问题。

当然，其也有对偶问题和解的稀疏性，不展开了。

如何使用SVM

我们已经知道，在分类问题中，通过解支持向量机基本型的对偶问题，可以得到“最优的”线性模型。

那么，如何使用SVM解决回归问题，即如何解决SVR（support vector regression）问题呢？这里需要使用“软间隔支持向量机”来寻找该线性模型。

基本思路与软间隔支持向量机类似，可以容忍超平面一定程度上的错误，认为其回归正确。

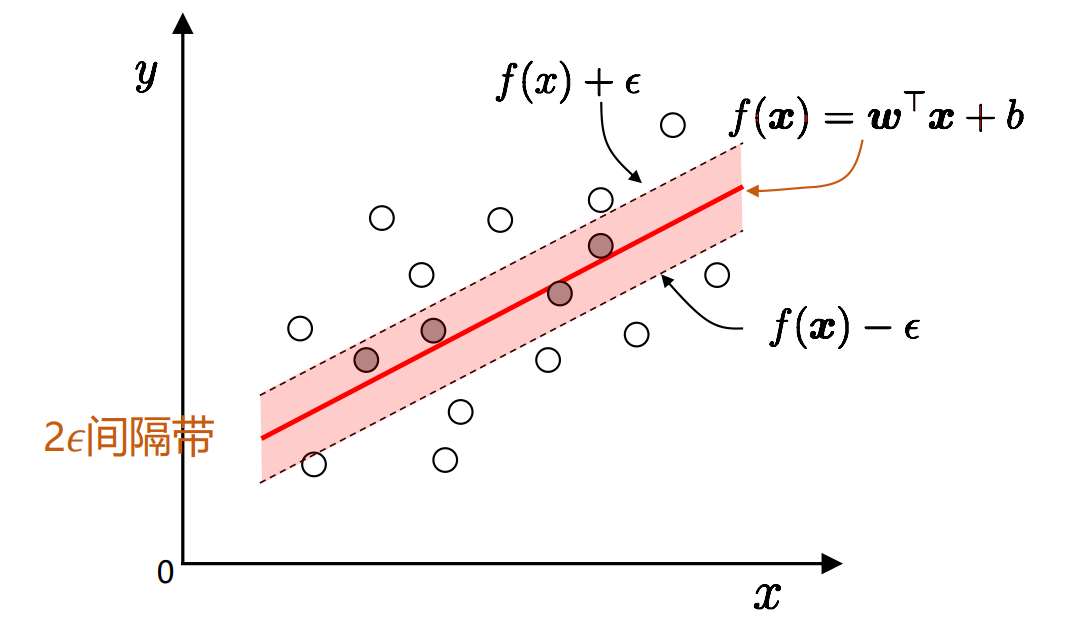
于是，可以将该思路形式化为

其中，$C$为正则化常数，$\ell_\epsilon$为$\epsilon$-不敏感损失函数。

$\ell_\epsilon$的表达式，及其与平方损失函数的比较如下：

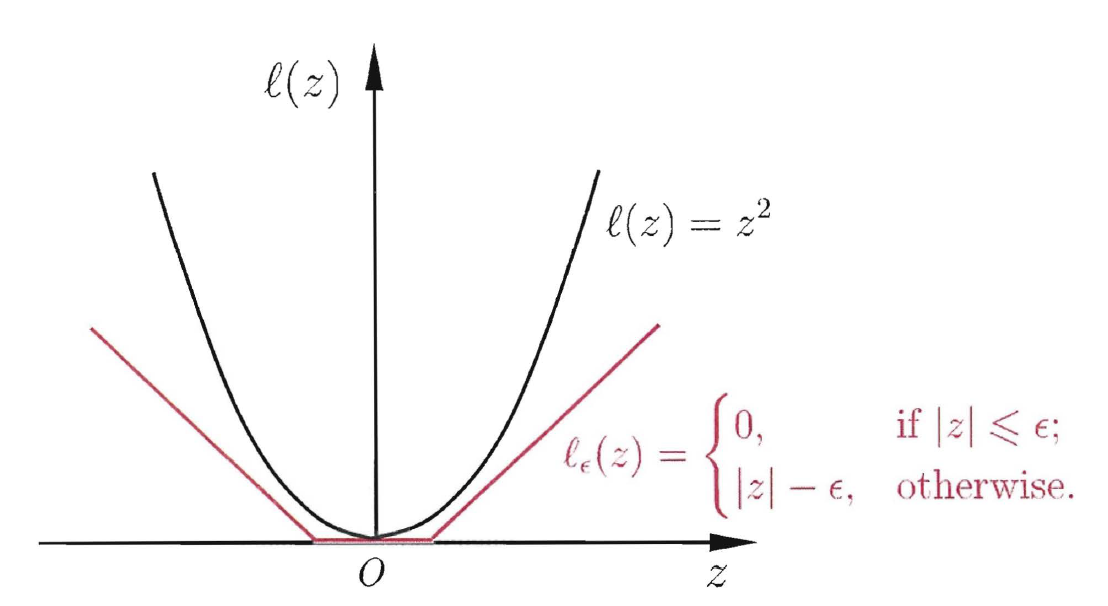
引入松弛变量$\xi_i$和$\hat{\xi_i}$，得到SVR问题的原问题

Note. 两个松弛变量，代表样本$\boldsymbol{x}_i$在预测变量（纵轴）上的，距$2\epsilon$间隔带的偏离程度（上方或下方），间隔带两侧的松弛程度可有所不同。

与支持向量机问题类似，引入四个拉格朗日乘子$\mu_i \geqslant 0, \hat{\mu}_i \geqslant 0, \alpha_i \geqslant 0, \hat{\alpha}_i \geqslant 0$，有拉格朗日函数

进而得到对偶问题

Note. 大于等于0是$\alpha$的条件，小于等于C是由$\mu$的条件+平稳条件得到的。（也可以写四条对偶问题可行条件）

平稳条件

原问题可行性条件

对偶问题可行性条件

互补松弛条件

综上，再将互补松弛条件中的$\mu_i$和$\hat{\mu_i}$用平稳条件中的$\alpha_i$和$\hat{\alpha_i}$代替，再因样本只能处在间隔带的一侧，所以$\alpha_i$和$\hat{\alpha_i}$至少有其一为0，进而$\xi_i$和$\hat{\xi_i}$至少有其一为0，所以KKT条件为

带着KKT条件解对偶问题，解得$\alpha_i^$和$\hat{\alpha}_i^$，其与原问题的解相对应，所以

与基本型类似地，选取任意一个满足$0\leqslant\alpha_i\leqslant C$的样本$(\boldsymbol{x}_i, y_i)$，有

也可以选取多个取平均值，有

综上，得到SVR问题的回归超平面模型

测试

题4

image-20221111104158469

题7

支持向量机对偶问题得到的目标函数最优值是原始问题目标函数最优值的____（上界/下界）

正确答案:[ “下界” ]

支持向量机对偶问题

读作：最大化（max）$L$的下确界（inf），同时使得$\mu \succeq 0$，求此时$\mu$的最优值$\mu^*$。

题11

对于两个样本点(0,0),(1,1)，若我们将其投影到与高斯核函数$\kappa(\boldsymbol{x}, \boldsymbol{y})=e^{-|x-y|^2}$关联的RKHS中时，则两个样本投影后的点距离为____（保留三位小数）

正确答案:[ “1.315” ]

题12

试判断定义在$\mathbf{R}^N \times \mathbf{R}^N$上的函数$\kappa(\boldsymbol{x}, \boldsymbol{y})=\left(\boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}+1\right)^2$是否为核函数。（是/否）

正确答案:[ “是” ]

典型的多项式核函数

题13

试判断定义在$\mathbf{R}^N \times \mathbf{R}^N$上的函数$\kappa(\boldsymbol{x}, \boldsymbol{y})=\left(\boldsymbol{x}^{\mathrm{T}} \boldsymbol{y}-1\right)^2$是否为核函数。（是/否）

正确答案:[ “否” ]

暂时不会

神经网络

这一章在大三上学期写过博客机器学习基础，这里就写的简单一点。

神经网络模型

Q：什么是神经网络？

A：神经网络是由具有适应性的简单单元组成的广泛并行互连的网络，它的组织能够模拟生物神经系统对真实世界物 体所作出的交互反应。[T. Kohonen, 1988]

M-P神经元模型

激活函数/挤压函数

logistic函数/对数几率函数

其导函数=将样本分为正例的可能性*将样本分为负例的可能性

几率odds=将样本分为正例的可能性/将样本分为负例的可能性

多层前馈网络结构

网络结构+神经元模型=神经网络

神经网络的层数：一般指含功能神经元的层的数量，“输入层”只是数据，不算层数。

万有逼近能力

多层前馈神经网络具有强大的表示能力（万有逼近能力）。

万有逼近定理（universal approximation theorem）：仅需一个包含足够多神经元的隐层，多层前馈神经网络就能以
任意精度逼近任意复杂度的（定义在紧集上的）连续函数[Hornik et al., 1989]。

推广：任何一个图灵可计算的（Turing computable）问题，都可以找到一个神经网络作为它的求解器。

但如何设置隐层神经元的个数是未决问题（open problem），常采用“试错法”（trial-by-error）调整。

万有逼近能力是用神经网络解决问题的可行性的前提，而不是“优势”。很多求解方法都有万有逼近能力，如傅里叶变换、泰勒展开、决策树等。我们证明神经网络具有万有逼近能力，是为了证明它具有可解释性，它一定可以找到参数去逼近目标函数。

BP算法推导

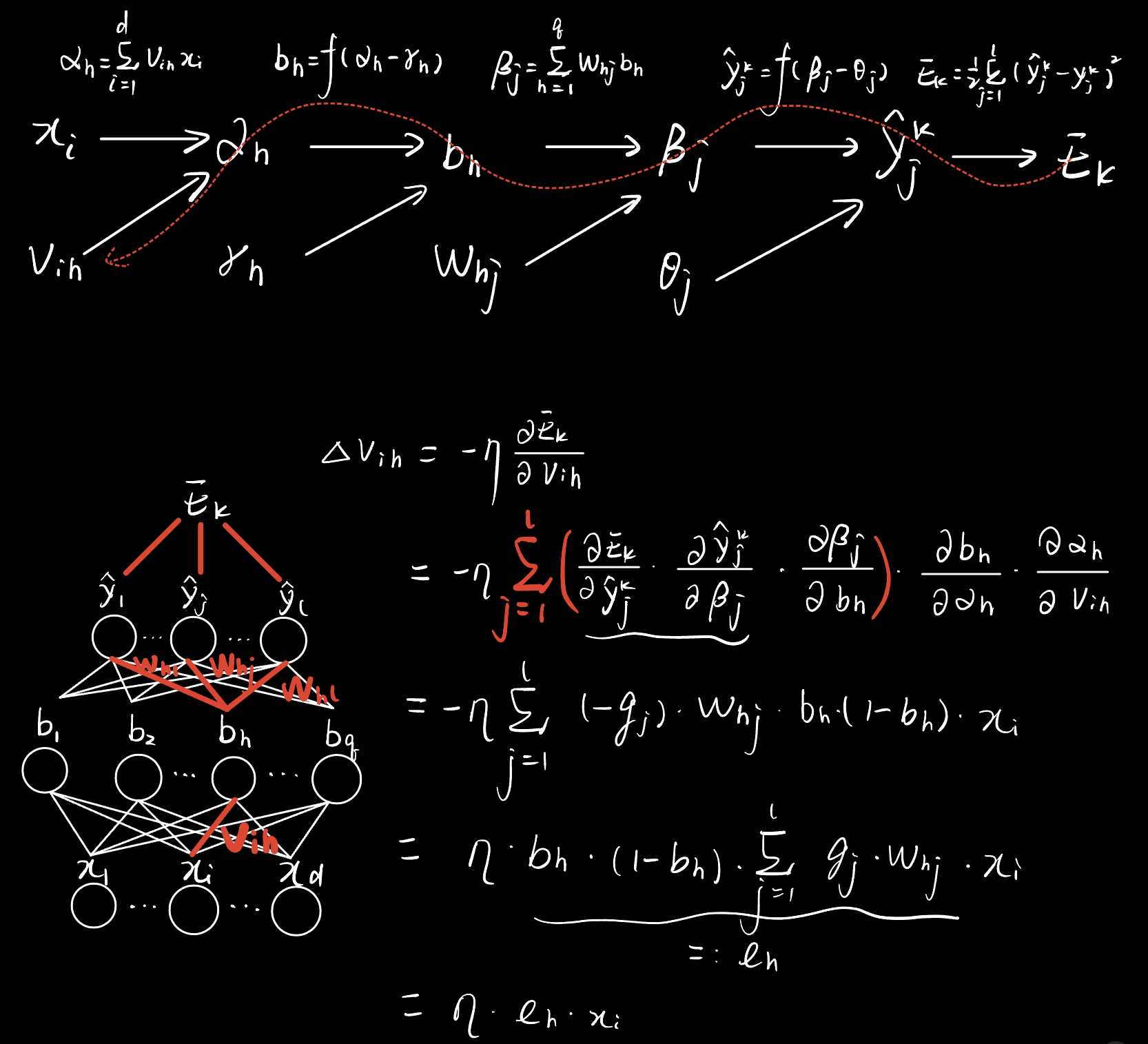
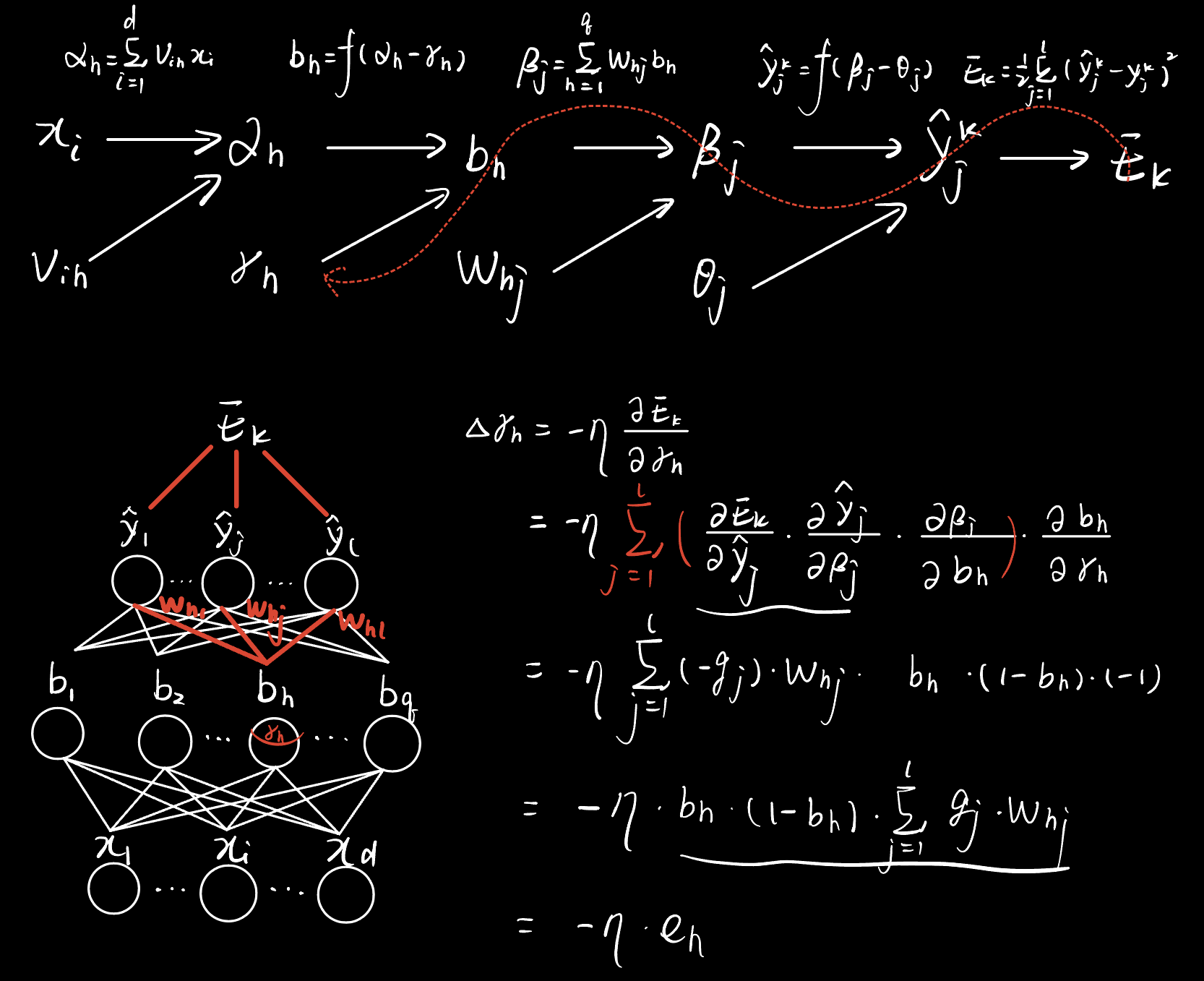
（这里不写了，可以参见我之前写的内容BP神经网络-误差反向传播算法）

贴一下另外三个更新公式中的增量的手写版推导过程。

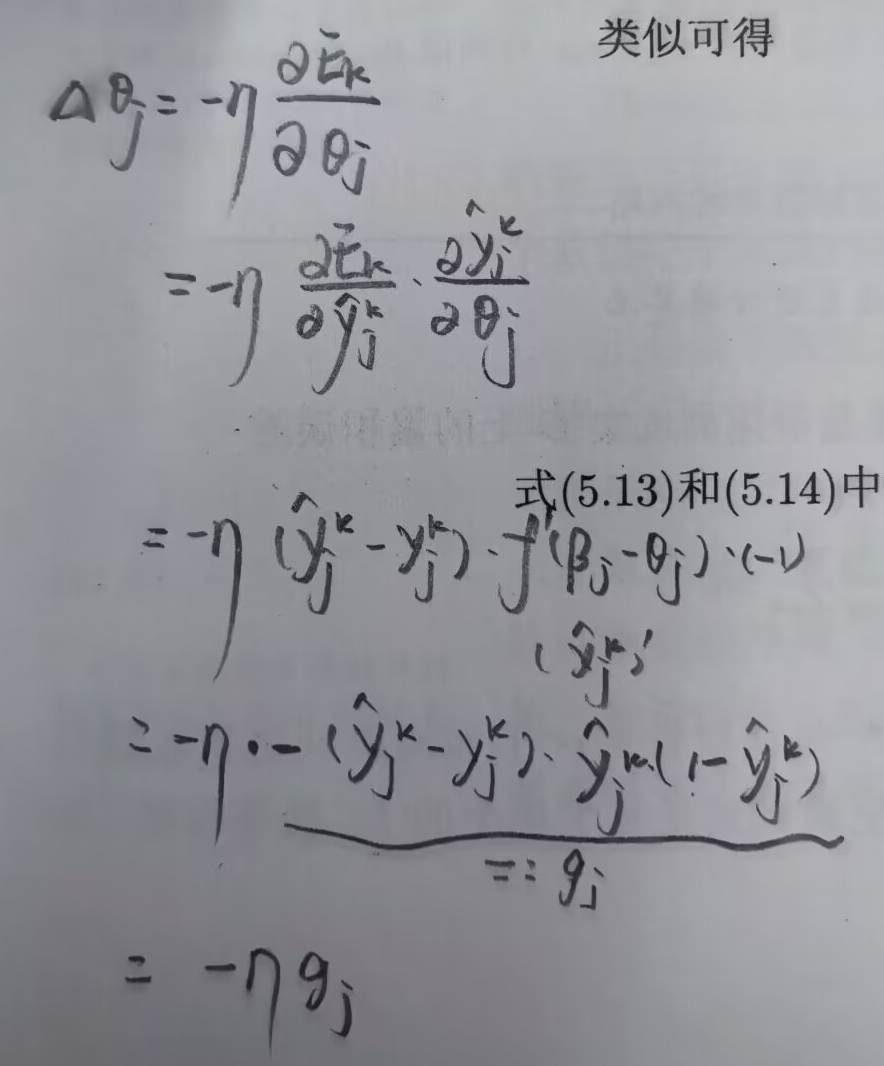
测试

题6

Sigmoid函数在 x=0.5 处的导数值为____(保留3位小数)。

正确答案:[ “0.235” ]

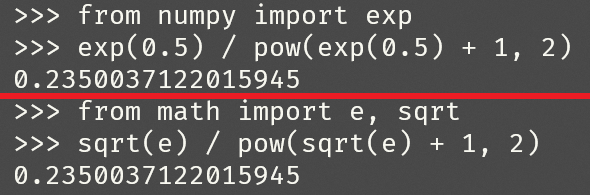
题9

考虑一个有1个输入结点、1个隐层结点、1个输出结点构成的神经网络，该网络输入到隐层的权重与隐层到输出的权重共享，即该神经网络的前馈表达式为$f(x)=\sigma\left(w \sigma\left(w x+b\right)+b\right)$，其中$\sigma(x)$为Sigmoid激活函数。考虑由两个样本组成的数据集$D=\{(0,0.5),(1,0.25)\}$，神经网络初始化参数为$w = -1, b = -1$，使用平方损失作为损失函数 (总损失为所有样本的平方和损失，不除以2)。则该神经网络在初始化下的损失为____(保留3位小数)。

正确答案:[ “0.079” ]

按照前面的记号，将神经网络形式化出来。

Note. 这里的$b$重复了，白色的$b$代表隐层神经元的输出，红色的$b$代表隐层和输出层的具体阈值。$w$虽然也重复了，但是因参数共享，意义上仍是共有的权重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
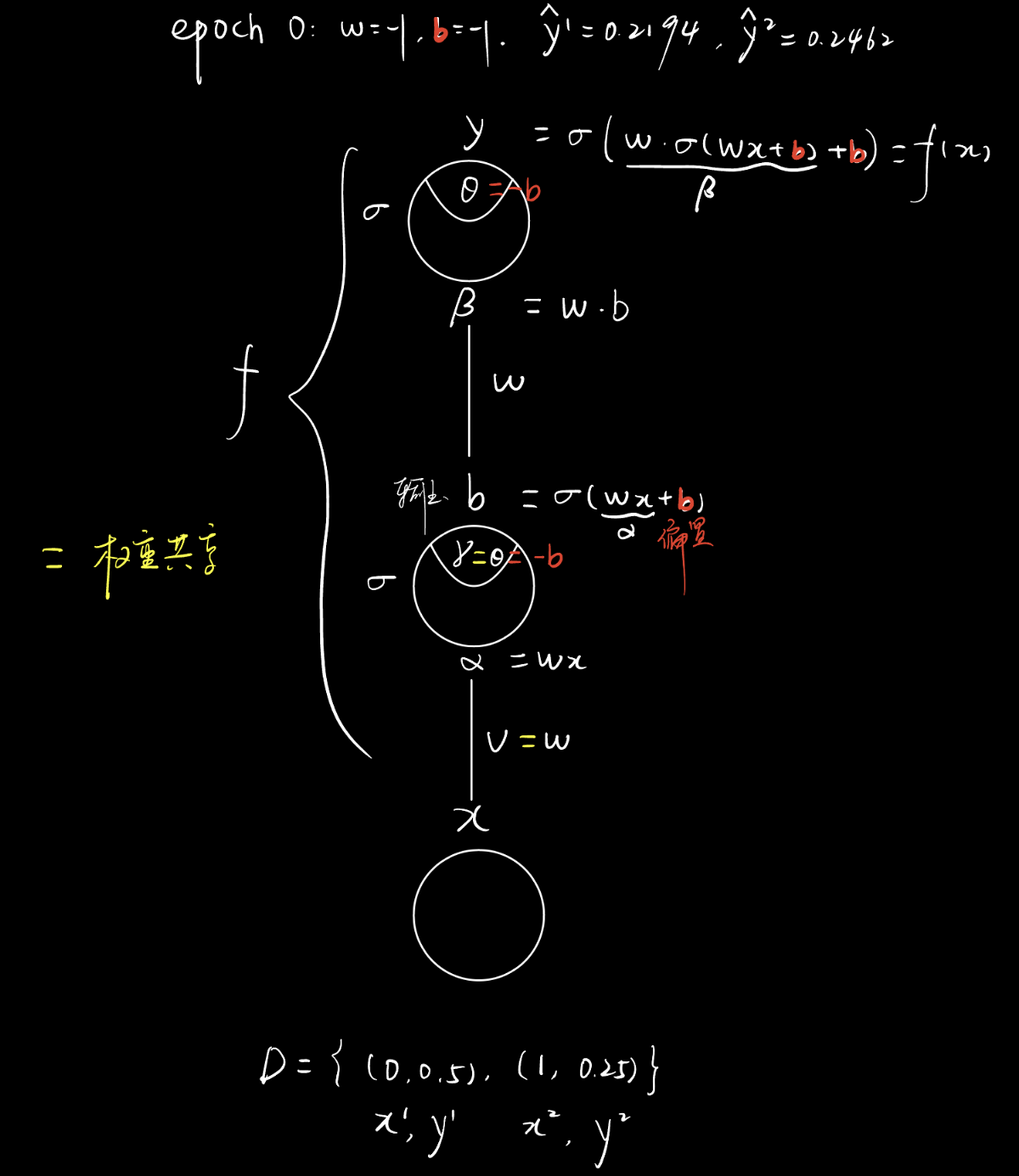
28
from math import e


def logistic(x):
    return 1 / (1 + pow(e, -x))

w, b = -1, -1
def f(x):
    '''
    初始化的神经网络所拟合的函数
    '''
    return logistic(w * logistic(w * x + b) + b)

def loss(y_hat, y):
    '''
    每个样本的平方损失 不除以2
    '''
    return pow(y_hat - y, 2)

dataset = ((0, 0.5), (1, 0.25))

if __name__ == '__main__':
    total_loss = 0
    for x, y in dataset:
        # print(f(x), y, loss(f(x), y))
        total_loss += loss(f(x), y)

    print(total_loss)

手算的话，要求保留三位小数，那么运算过程最好多保留一位。

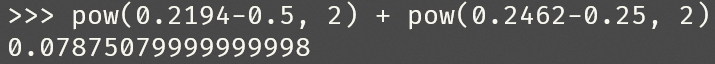
Note. 我以前做物理实验的时候是多保留两位的，很rigorous，最终分数在全校四千多修这门课的人中排名第一。

题10

上述损失关于$\omega$的偏导在初始点处的取值为____(保留3位小数)。
正确答案:[ “-0.026” ]

Note. 题10和题11，因为参数共享会导致偏导数加法，我建议还是不要用网络结构的链式法则求偏导数，还是把这个神经网络看做普通函数$f$来求偏导数好做。

这里就只写法二了，法一见题11。

1
2
3
4
5
6
7
8
9
10
11
12
13
from solve_6_9 import *


if __name__ == '__main__':
    init_point = dataset[0]
    ip_x, ip_y_gt = init_point[0], init_point[1]
    ip_y_hat = f(ip_x)
    g_net = -(ip_y_hat - ip_y_gt) * ip_y_hat * (1 - ip_y_hat)
    b_net = logistic(w * ip_x + b)
    e_net = b_net * (1 - b_net) * g_net * w
    
    # print(-2 * g_net * (b_net + w * b_net * (1 - b_net) * ip_x))
    print(-2 * (g_net * b_net + e_net * ip_x))

题11

上述损失关于$b$的偏导在初始点处的取值为____(保留3位有效数字)。

正确答案:[ “-0.078” ]

1
2
3
4
5
6
7
8
9
10
11
12
13
from solve_6_9 import *


if __name__ == '__main__':
    init_point = dataset[0]
    ip_x, ip_y_gt = init_point[0], init_point[1]
    ip_y_hat = f(ip_x)
    g_net = -(ip_y_hat - ip_y_gt) * ip_y_hat * (1 - ip_y_hat)
    b_net = logistic(w * ip_x + b)
    e_net = b_net * (1 - b_net) * g_net * w
    
    # print(-2 * g_net * (w * b_net * (1 - b_net) + 1))
    print(-2 * (e_net + g_net))

题12

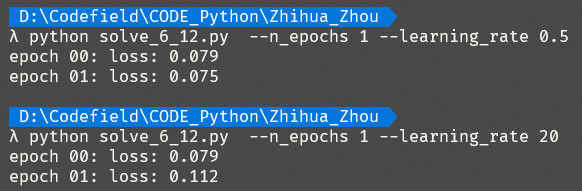
当步长取为0.5时，使用BP算法更新神经网络模型后，模型的损失为____ (保留3位小数)。

正确答案:[ “0.075” ]

Note. 题12和题13，使用累计误差反向传播算法，解题code写在一起了。

题13

当步长取为20时，使用BP算法更新神经网络模型后，模型的损失为____ (保留3位小数)。

对比上述两种步长值，体会步长选取与振荡现象的关系。

正确答案:[ “0.112” ]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
from math import e
import argparse


def logistic(x):
    return 1 / (1 + pow(e, -x))

def f(x):
    '''
    神经网络所拟合的函数，前向传播
    '''
    return logistic(w * logistic(w * x + b) + b)

def loss(y_hat, y):
    '''
    每个样本的平方损失 不除以2
    '''
    return pow(y_hat - y, 2)

dataset = ((0, 0.5), (1, 0.25))

def get_args():
    parser = argparse.ArgumentParser()

    parser.add_argument('--n_epochs', type=int, default=1)
    parser.add_argument('--learning_rate', type=float, default=0.5)

    args = parser.parse_args()

    return args


if __name__ == '__main__':
    args = get_args()

    n_epochs = args.n_epochs
    lr = args.learning_rate         # \eta
    w, b = -1, -1
    
    # loss on initialized net
    total_loss = 0
    for x, y in dataset:
        y_hat = f(x)
        total_loss += loss(y_hat, y)
    print("epoch {:02d}: loss: {:.3f}".format(0, total_loss))

    for epoch in range(n_epochs):
        # train
        # 累计误差反向传播
        delta_w, delta_b = 0, 0
        for x, y in dataset:
            # 反向传播
            y_hat = f(x)
            g_net = -(y_hat - y) * y_hat * (1 - y_hat)
            b_net = logistic(w * x + b)
            e_net = b_net * (1 - b_net) * g_net * w

            dw = -2 * (g_net * b_net + e_net * x)
            db = -2 * (e_net + g_net)
            delta_w += -lr * dw
            delta_b += -lr * db
        # 标准梯度下降
        w += delta_w
        b += delta_b

        # test
        total_loss = 0
        for x, y in dataset:
            y_hat = f(x)
            total_loss += loss(y_hat, y)
        print("epoch {:02d}: loss: {:.3f}".format(epoch + 1, total_loss))

贝叶斯分类器

贝叶斯决策论

贝叶斯决策论（Bayesian decision theory）是一种在概率框架下实施决策的基本方法。

下面在多分类任务下，介绍基本原理。

假设有$N$种可能的类别标记，即有$\mathcal{Y} = \lbrace c_1, c_2, \ldots, c_N\rbrace$。

记$\lambda_{ij}$为：因将标记为$c_j$的样本错误分类为$c_i$所产生的损失。

记$P(x)$为：样本$x$被错误分类为$c_i$类的概率。

记$P_0(x)$为：产生$x$，这个事件发生的概率。

那么基于后验概率$P_0(\lambda_{ij})=P\left(c_j \mid \boldsymbol{x}\right)$，可以得到错误分类所产生的损失的期望，即期望损失$E(\Lambda_{ij})$。在决策论中，也称其为在样本$\boldsymbol{x}$上的“条件风险”，记作$R\left(c_i \mid \boldsymbol{x}\right)$。

Note. $P_0(\lambda_{ij})=P\left(c_j \mid \boldsymbol{x}\right)$即为：产生$\lambda_{ij}$的概率 和 样本$x$是$c_j$类，被错误分类为$c_i$类的概率，二者意义相同。

对于每个样本$\boldsymbol{x}$，只要找到$c$类，让“将$\boldsymbol{x}$分到$c$类所面对的风险$R\left(c \mid \boldsymbol{x}\right)$”最小，那么$c$类就应该是分类器应该将$\boldsymbol{x}$划分到的类别。

将上述目标形式化，即可得到贝叶斯判定准则（Bayes decision rule）

其中，$h^\ast(\boldsymbol{x})$称为贝叶斯最优分类器（Bayes optimal classifier），用于得到样本$\boldsymbol{x}$的最优分类。与其对应的总体风险$R(h^\ast)$称为贝叶斯风险（Bayes risk），进而可用$1 - R(h^\ast)$反映分类器所能达到的最好性能，即训练所得模型的精度的理论上限。

生成式和判别式模型

如果所有后验概率$P\left(c \mid \boldsymbol{x}\right)$都能拿到真实值，那么根据贝叶斯判定准则做出的决策是理论上最好的决策，但$P\left(c \mid \boldsymbol{x}\right)$在现实中不易获得。

那么，从贝叶斯决策论的角度，机器学习要做的，就是基于有限的训练样本，尽可能准确地估计后验概率$P\left(c \mid \boldsymbol{x}\right)$。

在该角度下，机器学习模型可以按两种基本策略划分：判别式模型（Discriminative Models）、生成式模型（Generative Models）。

判别式模型

思路：直接对$P\left(c \mid \boldsymbol{x}\right)$建模。即直接估计样本$\boldsymbol{x}$被划分为某个类$c$的概率。

代表：

  • 决策树
  • BP神经网络
  • SVM

生成式模型

思路：先对联合概率分布$P(\boldsymbol{x}, c)$建模，再由此获得$P\left(c \mid \boldsymbol{x}\right)$。即先复原真实分布，再由条件概率公式得到类别。

代表：贝叶斯分类器

Note. 这里的“生成式”与“生成对抗网络”的“生成”是两回事。

由贝叶斯定理（由两个条件概率公式可以推出），可以得到

其中，

$P(c)$，是类“先验”（prior）概率，代表样本空间中$c$类样本所占的比例，可由大数定律、i.i.d.条件由频率估计出概率

$P(\boldsymbol{x} \mid c)$， 是样本$\boldsymbol{x}$相对于类标记$c$的类条件概率（class-conditional probability），或称为“似然”（likelihood，现代中文译作“可能性”）

$P(\boldsymbol{x})$，是用于归一化（所有c的分子之和/积分，除以它为1）的“证据”（evidence）因子

贝叶斯分类器与贝叶斯学习

统计学分为两大学派：频率主义学派（Frequentist）、贝叶斯主义学派（Bayesian）

频率学派认为参数是未知的定值，并通过一些统计方法来估计它们的值。

贝叶斯学派认为参数是未知的随机变量，需要先假设其分布作为“prior beliefs”，接着对新事件进行预测，根据它们得到参数的后验分布。

一句话解释：

贝叶斯主义在无法重复实验的时候是很有效的，但有时也是搞笑的，比如：

佐治亚理工学院的贝叶斯课程：BAYESIAN STATISTICS FOR ENGINEERS，里面有一页“Bayesian Fun”很有趣，其中一句笑话如下。

A Bayesian is one who, vaguely expecting a horse, and catching a glimpse of a donkey, strongly believes he has seen a mule.

贝叶斯学家是这样的人，他大概期待着想看见一匹马，然后他瞥见了一头驴，然后楞说自己看见了一只骡子。

（$posterior \propto likelihood \times prior$。先相信，再似然修正，最后得到后验）

再如一张漫画，来自https://xkcd.com/1132/

L is a Frequentist, R is a Bayesian.

L: This neutrino（中微子） detector measures whether the sun has gone nova（新星）.

R: Then, it rolls two dice（骰子）. If they both come up six, it lies to us. Otherwise, it tells the truth.

L: Let’s try. Detector! Has the sun gone nova?

L: The probability of this result happening by chance is $\frac{1}{36}=0.027$. Since $p<0.05$, I conclude that the sun has exploded.

R: Bet you $50 it hasn’t.

翻译版：

因为贝叶斯学习中先验分布的选择是困难的，所以在贝叶斯分类器中，先验分布采用了频率主义的估计方法。

Note. 出自PRML中文版P23。

即贝叶斯分类器同时使用了统计学习方法和贝叶斯学习方法。不完全属于贝叶斯学习。

极大似然估计

Q：如何估计关于类别$c$的类条件概率$P(\boldsymbol{x} \mid c)$呢？

A：一种常用的策略是，假定该概率具有确定的概率分布形式（如高斯分布/正态分布），然后基于训练样本对其参数进行估计。

设$P(\boldsymbol{x} \mid c)$具有确定的形式，且被参数向量$\boldsymbol{\theta}_c$唯一确定。那么，可以将其记为$P(\boldsymbol{x} \mid \boldsymbol{\theta}_c)$，我们的任务是使用训练集$D$估计参数$\boldsymbol{\theta}_c$。

下面介绍频率学派的极大似然估计（MLE, Maximum Likelihood Estimation），它是根据数据采样（$D$）估计概率分布参数（$\boldsymbol{\theta}_c$）的经典方法。

记$D_c$为$D$中类别为$c$的样本的集合，假设其i.i.d，则生成的样本类别为$c$是独立随机事件，有

Note. 乘积product符号的LaTeX代码\prod。

对$\boldsymbol{\theta}_c$进行极大似然估计，即

连乘操作在计算机中容易出现数值下溢，所以通常使用“对数似然”（Log-Likelihood）进行估计。

此时，对$\boldsymbol{\theta}_c$进行极大似然估计，即

举例。

在属性为连续值时，设$p(\boldsymbol{x} \mid c) \sim \mathcal{N}(\boldsymbol{\mu}_c, \boldsymbol{\sigma}_c^2)$，则$\boldsymbol{\theta}_c = (\boldsymbol{\mu}_c, \boldsymbol{\sigma}_c^2)$，其形式为

其中，$d$表示$x$的dimension；$\boldsymbol{\Sigma}_c = \boldsymbol{\sigma}_c^2$，为对称正定协方差矩阵；$|\boldsymbol{\Sigma}_c|$表示$\boldsymbol{\Sigma}_c$的行列式。

那么，分布参数们的极大似然估计为

以下只是解优化函数的流程，具体推导见南瓜书。

根据$|D_n| = n$, $\boldsymbol{x}^\mathrm{T}\boldsymbol{A}\boldsymbol{x} = \operatorname{tr}\left(\boldsymbol{A}\boldsymbol{x}\boldsymbol{x}^\mathrm{T}\right)$, $\bar{x} = \frac{1}{n}\sum_{i=1}^{n}\boldsymbol{x}_i$，得最终化简式

由二次型的性质知，当且仅当$\boldsymbol{\mu}_c-\overline{\boldsymbol{x}} = 0$时，上式最后一项取最小值$0$，因此得

将其代回优化函数，有

由一引理（详见南瓜书或张伟平《多元正态分布参数的估计和数据的清洁与变换》slide）知，当且仅当$\boldsymbol{\Sigma}_c=\frac{1}{n} \sum_{i=1}^n\left(\boldsymbol{x}_i-\overline{\boldsymbol{x}}\right)\left(\boldsymbol{x}_i-\overline{\boldsymbol{x}}\right)^{\mathrm{T}}$时，优化函数整体取最小值，因此得

综上，有

最后，极大似然估计只估计分布的参数，因此其准确性取决于事先所假设的分布，这需要对具体应用任务的经验。

朴素贝叶斯分类器

但是，类条件概率$P(\boldsymbol{x} \mid c)$是所有属性上的联合概率。在有限的$D$上估计联合概率，会遭遇组合爆炸和样本稀疏问题，即$2^d \gg m$。

因此，朴素贝叶斯分类器（Naïve Bayes Classifier）采用了“属性条件独立性假设”（attribute conditional independence assumption）：对已知类别，假设所有属性相互独立。即假设每个属性独立地对分类结果产生影响。

基于此，可将后验概率写作

因$P(\boldsymbol{x})$与类别$c$无关，所以最小化分类错误率的朴素贝叶斯分类器为

记$D_c$为$D$中类别为$c$的样本组成的集合，设该集合i.i.d，有

对于离散属性，记$D_{c, x_i}$为$D_c$中在第$i$个属性上取值为$x_i$的样本组成的集合，有

对于连续属性，仍需假设概率密度函数。如假设$p(x_i \mid c) \sim \mathcal{N}(\mu_{c, i}, \sigma_{c, i}^2)$，与上一节类似，$\mu_{c, i}$和$\sigma_{c, i}^2$分别表示类别为$c$的样本在第$i$个属性上的取值的均值和方差，有

基于“属性条件独立性假设”，用频率求$P(c \mid \boldsymbol{x})$具有一种问题：如果测试例中出现了某个$x_{i, new}$，它没有在$D$中的任何一个$\boldsymbol{x}$中出现过。那么在测试时，因$P(x_{i, new} \mid c) = 0$，将导致$P(c \mid \boldsymbol{x}) = 0$ 。这样的话，即使其他属性都表示它像类别$c$（其他的$P$很大），但朴素贝叶斯分类器因该值为$0$，不可能达到$\max$，所以不会将其分类为$c$。

为了修正这种其他属性携带的信息（$P \neq 0$）被训练集中未出现的属性值所带来的信息（$P = 0$）所“抹去”的问题，我们使用“拉普拉斯修正”（Laplacian correction）对估计的概率值进行“平滑”（smoothing）处理。

记$N$为$D$中可能的类别数；$N_i$为（$D$中）第$i$个属性值可能的取值数。则有拉普拉斯修正概率

这个式子其实很好理解：分子+1，防止概率估计值为0；分母+类别数量，防止类别变多时偏离实际估计值（从极限角度考虑。例如，假设$D$中样本的类别多到各不相同，则$\hat{P}(c) =\frac{1+1}{N\boldsymbol{+N}}$，分母+类别数后，不会偏离原估计值$P(c) = \frac{1}{N}$）

测试

题11、12、13

考虑以上数据集。其中$x_1$与$x_2$为特征，其取值集合分别为$x_1 = \lbrace-1, 0, 1\rbrace$，$x_2 = \lbrace B, M, S\rbrace$。$y$为类别标记，其取值集合为$y=\lbrace 0, 1 \rbrace$。

11）使用所给训练数据，学习一个朴素贝叶斯分类器，考虑样本$\boldsymbol{x} = \lbrace 0, B\rbrace$，请计算$P(y=0)P(\boldsymbol{x} \mid y=0)$的值____（保留2位有效数字）。

12）使用所给训练数据，学习一个朴素贝叶斯分类器，这个分类器会将样本$\boldsymbol{x} = \lbrace 0, B\rbrace$的标记预测为____。

13）使用所给训练数据，使用“拉普拉斯修正”，学习一个朴素贝叶斯分类器，考虑样本$\boldsymbol{x} = \lbrace 0, B\rbrace$，请计算$\hat{P}(y=1)\hat{P}(\boldsymbol{x} \mid y=1)$的值____（保留2位有效数字）。

正确答案:[ “0.067”, “0”, “0.041” ]

11）

12）

显然有$P(y=0)P(\boldsymbol{x} \mid y=0) > P(y=1)P(\boldsymbol{x} \mid y=1)$，所以$\underset{c \in \mathcal{Y}}{\arg \max } \ P(c) \prod_{i=1}^d P\left(x_i \mid c\right) = 0$

13）

Note. Thomas Bayes这人很神奇，出生日期不确定，专业是逻辑学和神学（logic and theology），职业是牧师，研究数学是为了证明上帝的存在，获得了类似“英国科学院院士”（英国皇家学会会士）的荣誉称号。他晚年才对概率感兴趣，死后贝叶斯定理才被当做遗产宣读，直到二十世纪才受到重视。现在流传的画像都不确定是不是本人。

难怪贝叶斯理论中会有信念（beliefs）这样很不“数学”的词汇。我不知道有多少像贝叶斯这样的人，但我知道不论以什么目的、途径，只要有坚定的目标，就有可能做出有意义的研究。

集成学习

集成学习的结构

集成学习（Ensemble Learning，法语词源，其中Ensemble读作/ɑːnˈsɑːmb(ə)l/）：使用多个学习器解决问题的方法。

这种方法十分地类似现在各高校的committee制度，所以也被称作“基于委员会的学习”（committed-base learning）。

当学习器们的类型相同时，称它们是“同质的”（homo-）集成，个体学习器被称作“基学习器”，它们共同的学习算法称作“基学习算法”。

当学习器们的类型不同时，称它们是“异质的”（hetero-）集成，个体学习器被称作“组件学习器”。

集成学习往往可以在难以改进单个算法的情况下对具体任务提升准确度。如图，KDDCup历年的冠军几乎都使用了集成学习（蓝字）。

因此，

To win? Ensemble!

想赢？那就集成！

好而不同

以“多数投票”集成学习算法为例。

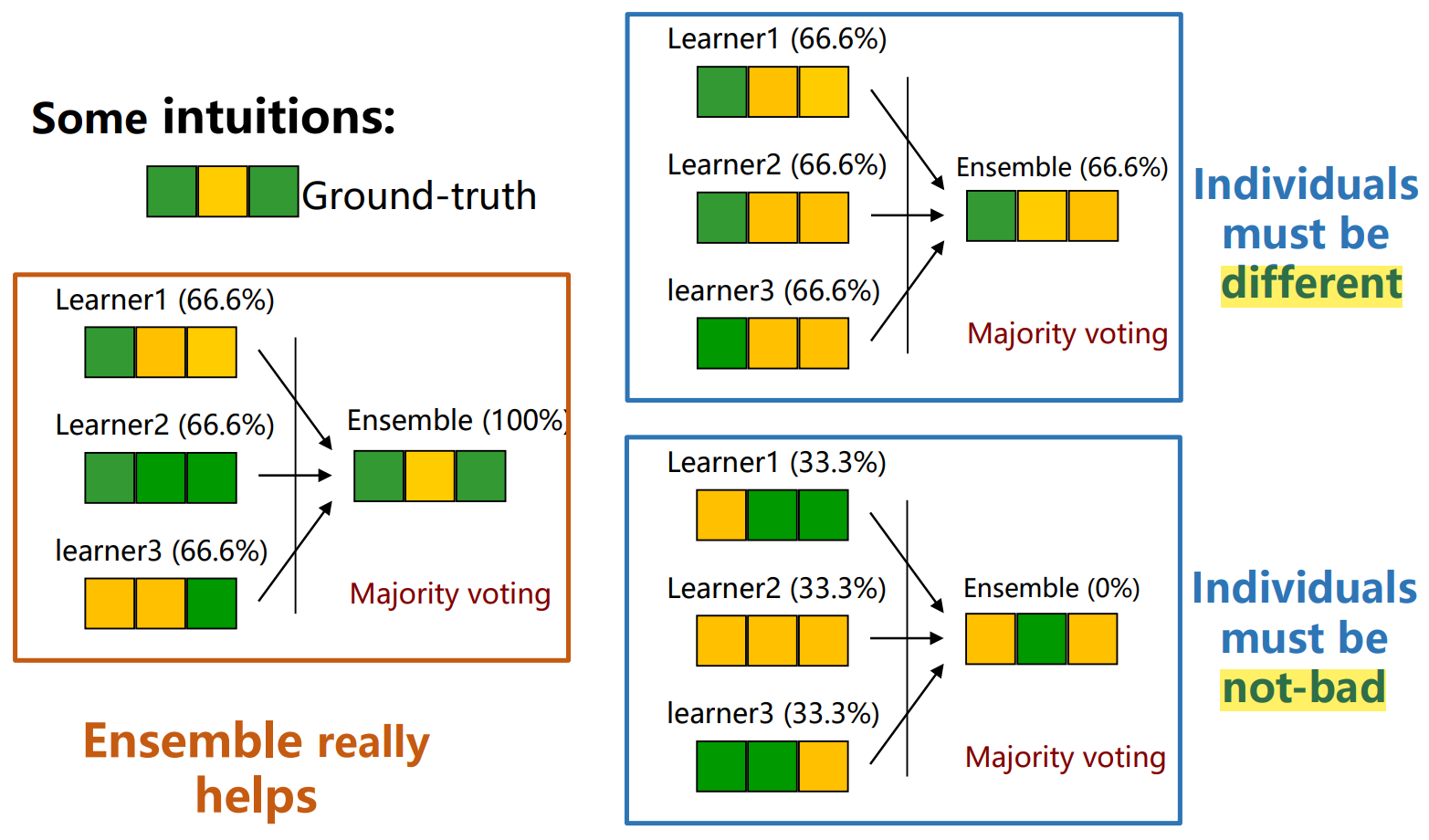
可以看出：当个体学习器们“不坏”且“不同”时，集成学习器的性能可能会比最好的个体学习器还要好；但当个体学习器们“相似”时，集成学习器的性能可能不会有提升；当个体学习器们“不好”时，集成学习器的性能甚至可能会下降。

因此，集成学习中的个体学习器们要“好而不同”。

误差-分歧分解（Error-Ambiguity Decomposition）可以用于衡量集成学习的性能。

其中，

$E$表示集成学习的错误率；

$\bar{E}$表示个体学习器的平均错误率；

$\bar{A}$表示个体学习器的“分歧”（ambiguity），即“多样性”（diversity）。

这也说明了：个体学习器们越准确，且差异越大，集成学习的性能越好。

但误差-分歧分解是直觉上的，且不易实现的。原因如下：

  1. ambiguity是用ground truth在数学上定义的。在没有ground truth时，没有可计算的定义。
  2. 该表达式只适用于以squared loss作为损失函数的回归问题。
  3. 当每个学习器在训练集上的err都很低（acc都很高）时，它们的预测结果高度相似，ambiguity自然也很低。也就是说，$\bar{E}$和$\bar{A}$是正相关的，不太容易找到二者的tradeoff，使集成学习的err最低。

两类常用集成学习算法

根据个体学习器的生成方式，目前的集成学习方法大致可分为两大类：序列化方法、并行化方法。

序列化方法：个体学习器间存在强依赖关系、必须串行生成的集成学习方法。

  • AdaBoost [Freund & Schapire, JcSS97]（代表性算法）
  • GradientBoost [Friedman, AnnStat01]（目前用的最多，竞赛上著名的XGBoost是它的一种工程实现）
  • LPBoost [Demiriz, Bennett, Shawe-Taylor, MLJO6]
  • …

并行化方法：个体学习器间不存在强依赖关系、可同时生成的集成学习方法。

  • Bagging [Breiman, MLJ96]（代表性算法）
  • Random Forest [Breiman, MLJO1]（目前用的最多）
  • Random Subspace [Ho, TPAMI98]
  • …

Boosting

Boosting是一族可将弱学习器提升为强学习器的同质的序列化集成学习算法。

Boosting的流程图图例（A flowchart illustration）

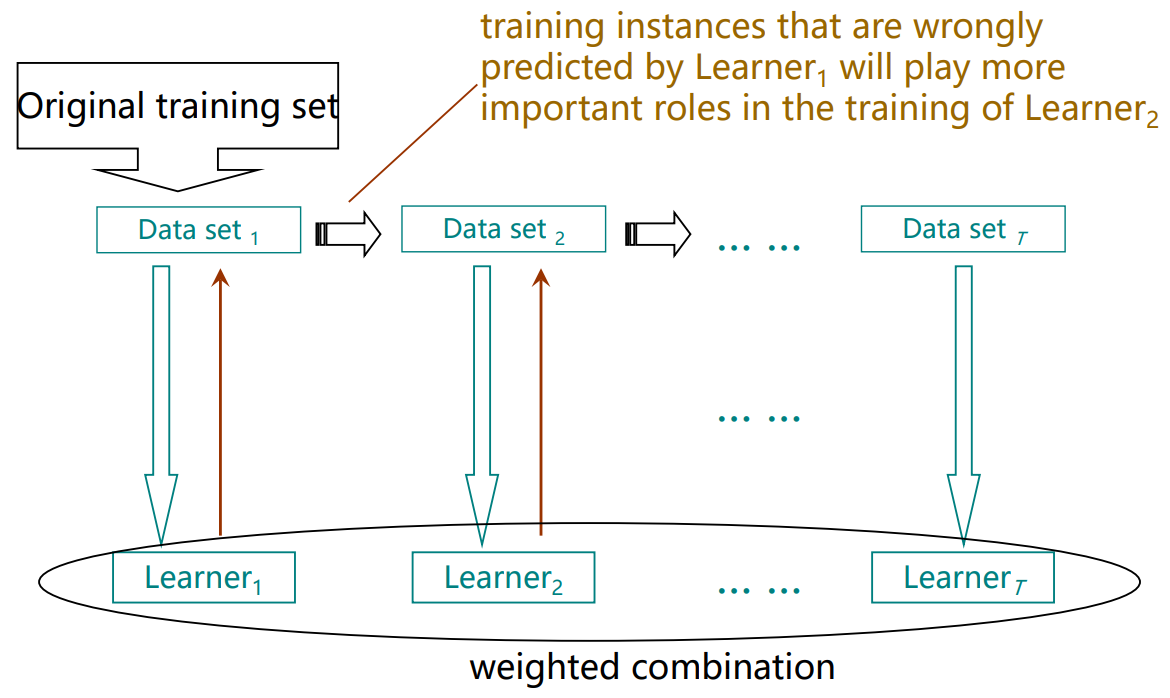
其主要思想即为：让某个学习器着重训练其上一个学习器预测错误的那些示例（不含gt的样例，见基本术语），最后将学习器们按权重结合。

为了着重训练这些示例，有两种思路：采样/带权。

因此Boosting目前有两类算法。

  1. 重采样法（re-sampling）：在训练的每一轮中，根据样本分布为训练集的每个训练样本重新赋予一个权重。
  2. 重赋权法（re-weighting）：在训练的每一轮中，根据样本分布对训练集重新进行采样。

通过某种方法形成新训练集后继续进行训练。

但是，需要注意：

  1. 有些基学习算法无法处理带权重样本，如神经网络。所以，要根据基学习算法选择采样还是带权；
  2. Boosting算法会检查每一轮生成的基学习器，如果基学习器不满足基本条件，则会结束训练。所以，“重赋权法”可能过早停止训练。但“重采样法”可以用旧训练集重新采样形成新训练集，再继续本轮训练，该方法称为重采样法的“重启动”。

最后，训练过程越后，基学习器的训练集中的样本越难分类，性能越差。所以，产生的基学习器们需要按权结合。

Bagging

Bagging是一种可将弱学习器提升为强学习器的同质的并行化集成学习算法。

Bagging的流程图图例

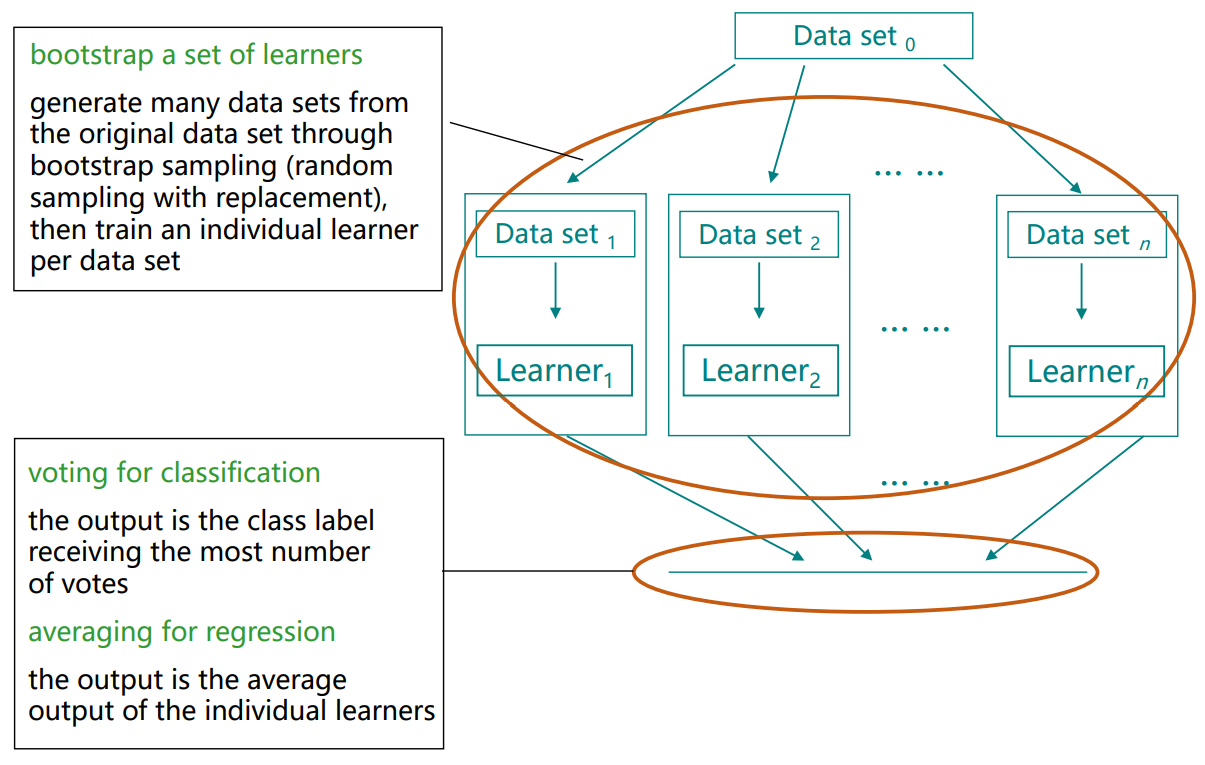
其主要思想即为：bootstrap sampling出n个相互有交叠的训练集，再根据它们训练出n个有差异的基学习器，最后根据任务类型对基学习器们做投票或平均。

最后，若处理分类问题，则对输出做投票确定类别；若处理回归问题，则对输出做平均（各基学习器的训练集地位相同）确定输出。

值得一提的是，bootstrap sampling过程中剩余的约36.8%的样本可用于验证集来对泛化性能进行估计，称为“包外估计”（out-of-bag estimate）[Breiman, 1996a; Wolpert and Macready, 1999]。为此，需要记录各基学习器未使用的训练样本。

事实上，包外样本还有许多其他用途，我也没有具体用过，详见西瓜书P179。

多样性度量

接“好而不同”节，讨论一下实践中如何对多样性$\bar{A}$进行度量。

度量个体分类器们的多样性，典型的做法是考虑个体分类器们的两两相似性/两两不相似性。

参照混淆矩阵，我们可以得到分类器$h_i$和$h_j$的预测结果列联表。

分类器$h_j$ \ 个数 \ 分类器$h_i$ $h_i = +1$ $h_i = -1$
$h_j = +1$ $a$ $c$
$h_j = -1$ $b$ $d$

其中，

$a$表示分类器$h_i$和$h_j$均预测为正类的样本数目；

$b$表示分类器$h_i$预测为正类、$h_j$均预测为负类的样本数目；

$c$表示分类器$h_i$预测为负类、$h_j$均预测为正类的样本数目；

$d$表示分类器$h_i$和$h_j$均预测为负类的样本数目。

多样性度量一般基于列联表定义，下面给出一些常见的多样性度量

  • 不合度量（disagreement measure）

  • 相关系数（correlation coefficient）

    Note. $\rho$的LaTeX表示是\rho

  • $Q$-统计量（$𝑄$-statistic）

  • $\kappa$统计量（$\kappa$-statistic）

    其中，$p_1$表示两分类器取得一致的概率；$p_2$表示两分类器偶然取得一致的概率（根据$D$估算）

对它们的具体描述详见西瓜书P187。

这四种都是”pair wise”的多样性度量，可以通过二维图片表示出来，如著名的$\kappa$-误差图。

在UCI数据集tic-tac-toe上的$\kappa$-误差图，每个集成含50棵C4.5决策树：

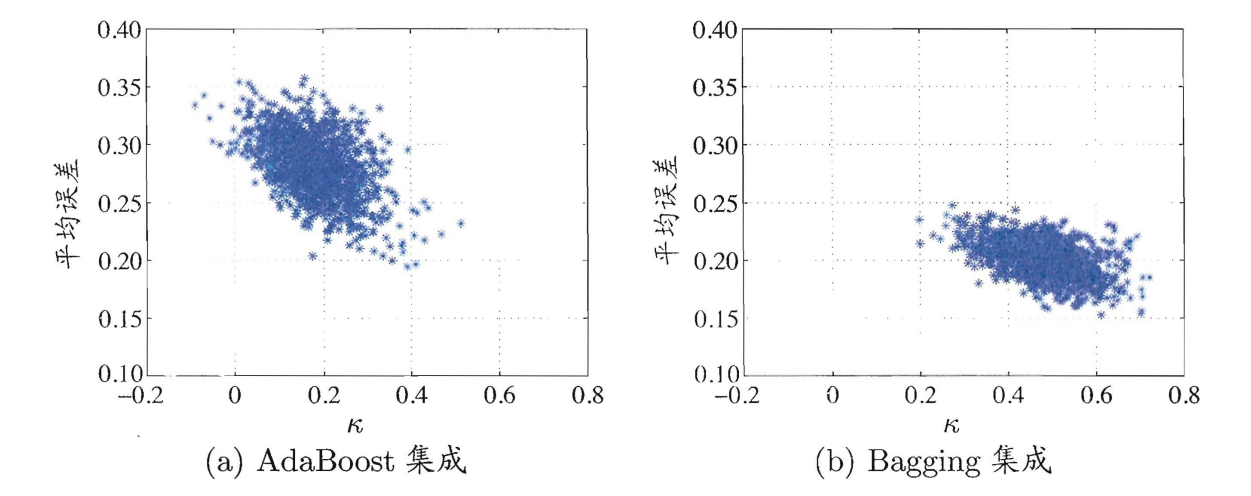
$\kappa$-误差图中将一对分类器作为一个点，其横坐标为它们的$\kappa$值，纵坐标为它们的平均误差。因此，数据点云的位置越高，则平均误差越大，准确性越低；数据点云的位置越右，则$\kappa$值越大，多样性越小。

因此，$\kappa$-误差图中的点云越靠左下，越“好而不同”。

测试

题6、题7

AdaBoost算法是一种常用的Boosting算法，该算法的伪代码如图所示，其中$Z_t$用于确保$D_{t+1}$是一个分布。考虑由3个样本组成的训练集，在第1轮中基学习算法将样本1与样本2分类正确，样本3分类错误。

6）在第2轮中，样本1的权重为____(保留3位小数)。

7）在第2轮中，样本3的权重为____(保留3位小数)。

正确答案:[ “0.250”, “0.500” ]

了解Boosting这一族算法的思想就比较容易理解AdaBoost算法了，只要把这几个变量的意义写出来就可以理解了。

伪代码中，

$\mathcal{D}_t(\boldsymbol{x})$代表第$t$轮中，所有样本的权重，是一个分布；

$\mathfrak{L}$是基学习算法，$\mathfrak{L}\left(D, \mathcal{D}_t\right)$代表基于分布$\mathcal{D}_t$，在$D$上训练；

$h_t$代表第$t$轮中，$\mathfrak{L}\left(D, \mathcal{D}_t\right)$生成出的基学习器/分类器；

$\epsilon_t$代表第$t$轮中，$h_t$预测结果的错误率；

$\alpha_t$代表$h_t$的权重；

$Z_t$代表第$t$轮中的规范化因子，用于确保$\mathcal{D}_{t+1}$是一个分布（样本权重之和为1）。

因此，计算过程如下。

初始化样本权重分布$\mathcal{D}_1(\boldsymbol{x})$

epoch 1：

按样本权重$w_i$计算错误率$\epsilon_1 $

Note. $\mathbb{I}$或$\mathbb{1}$（\mathbb{I}或\mathbb{1}）为指示函数，即

计算$h_1$的的权重/相关系数$\alpha_1$

更新样本权重，由

有

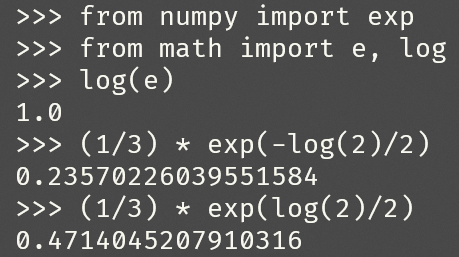
计算分布$\mathcal{D}_2$（权重归一化）

因此，在epoch 2中，$w_1 = 0.250$，$w_3=0.500$。

题8

弱学习器指泛化性能略优于随机猜测的学习器，如二分类问题中指精度略高于0.5的分类器。那么在三分类问题中，弱学习器是指精度略高于____ (保留3位小数) 的学习器。

正确答案:[ “0.333” ]

Highlight. 弱学习器指泛化性能略优于随机猜测的学习器。

题9

当样本足够多时，使用3个基学习器的Bagging算法用到的训练数据的比例为____(小数形式并保留3位小数)。

正确答案:[ “0.950” ]

考虑某个样本，它没有被三个基学习器bootstrap sampling的概率是

那么，其对立事件，即某个样本被bootstrap sampling的概率是

所以原始训练数据被bootstrap sampling到的比例是0.950。

聚类

聚类任务

聚类（Clustering）是无监督学习中的一种典型任务，其任务目标类似于有监督学习中的分类任务。

另外，有监督学习中的回归任务类似于无监督学习中的密度估计（density estimation）。

聚类的目标：将数据集中的样本划分为若干个不相交的子集，称为“簇”（cluster）。

如图，聚类就是将相似的样本们“物以类聚”。

聚类既可以作为一个单独过程，用于寻找数据内部的分布结构、寻找潜在的概念/类别；也可以作为分类等其他任务的前驱过程，即根据聚类结果将每个“簇”定义为一个“类”，形成有标注/标签数据，然后再基于这些标注数据训练出分类模型，用于判别未见样本。可用于电子商务中对新用户类型的判别。

聚类方法概述

首先，聚类的“好坏”不存在绝对标准。

5簇 2簇

如上两图，聚类为5簇/2簇都找到了样本潜在的概念：种类/颜色。因此，聚类的“好坏”只取决于用户的看法，对用户是否有帮助。

所以，聚类算法总能创造出很多新的标准，使旧的算法无法分成这种标准。

周志华老师写的关于聚类的故事。

老师拿来苹果和梨，让小朋友分成两份。

小明把大苹果大梨放一起，小个头的放一起，老师点头，嗯，体量感。

小芳把红苹果挑出来，剩下的放一起，老师点头，颜色感。

小武的结果？不明白。小武掏出眼镜：最新款，能看到水果里有几个籽， 左边这堆单数，右边双数。

老师很高兴：新的聚类算法诞生了！

因为实践中的聚类标准太多，很可能没有现成的聚类算法可用，所以我们要了解的是聚类有哪几种典型的思路。

常见的聚类方法：

  • 原型聚类（基于原型的聚类，prototype-based clustering）
    • 假设：样本内部结构能通过一组原型（有代表性的样本）刻画
    • 过程：先对原型初始化，然后对原型进行迭代更新求解
    • 代表：k均值聚类、学习向量量化（LVQ）、高斯混合聚类
  • 密度聚类（基于密度的聚类，density-based clustering）
    • 假设：样本内部结构能通过样本分布的紧密程度刻画
    • 过程：从样本密度的角度来考察样本之间的可连接性，并基于可连接样本不断扩展聚类簇
    • 代表：DBSCAN、OPTICS、DENCLUE
  • 层次聚类（hierarchical clustering）
    • 假设：样本能够产生不同粒度的聚类结果
    • 过程：在不同层次对数据集进行划分，从而形成树形的聚类结构
    • 代表：AGNES（自底向上）、DIANA（自顶向下）

原型聚类被研究得最多，且有概率上的良好解释，如高斯混合聚类就可从贝叶斯学习、统计学习角度解释，k均值聚类等都是高斯混合聚类的特殊情况。但原型聚类通常只能找出椭球形的/凸的聚类结构，不太能处理“香肠形”的/非凸的聚类结构。

生成数据 聚类结果

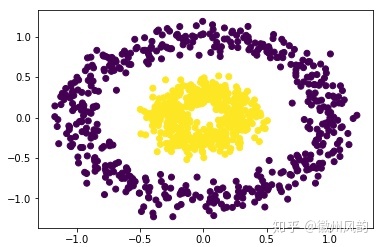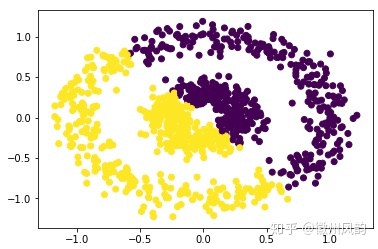测试

题14

下图所示聚类结构____（可以/不可以）通过标准型的k均值聚类算法得到。

注：标准型指不使用核方法。

正确答案:[ “不可以” ]

左下角的簇形状是非凸的，k均值聚类算法不可以聚类出非凸的簇。

题15

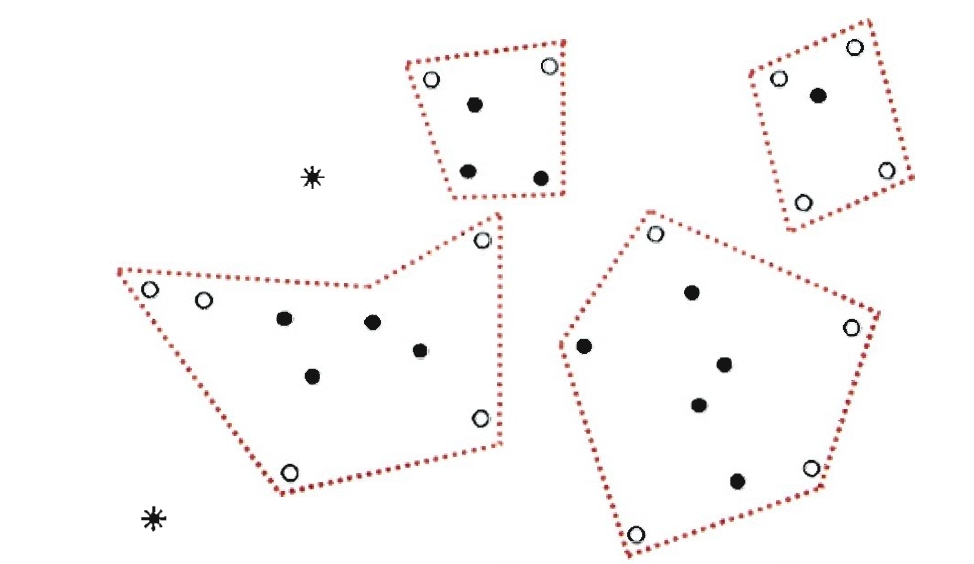
下图所示聚类结构最可能通过____（原型聚类/密度聚类/层次聚类）得到。

正确答案:[ “密度聚类” ]

下方聚类簇的形状是非凸的，密度聚类更适合处理非凸的样本。（而且我觉得如果是层次聚类肯定会给树状图，这个才是层次聚类的特征）

考试

感想

有始有终！总算弥补了科班但没学过ML的遗憾，自学太不容易了，嘤。

错了两道题，一个是没看清题，还有一个是答案错了，就是这道。

刚刚发现，如果免费学习的话，2023-03-10之后就不能复习题目了，最近会把所有的题单独开一个POST存起来，但是解析只在本POST里有。