BP神经网络

神经元模型

神经网络中最基本的成分是神经元模型。神经元模型源自“仿生”的思想，是对生物神经元的一种模仿。

首先，看一下生物学上的神经元。

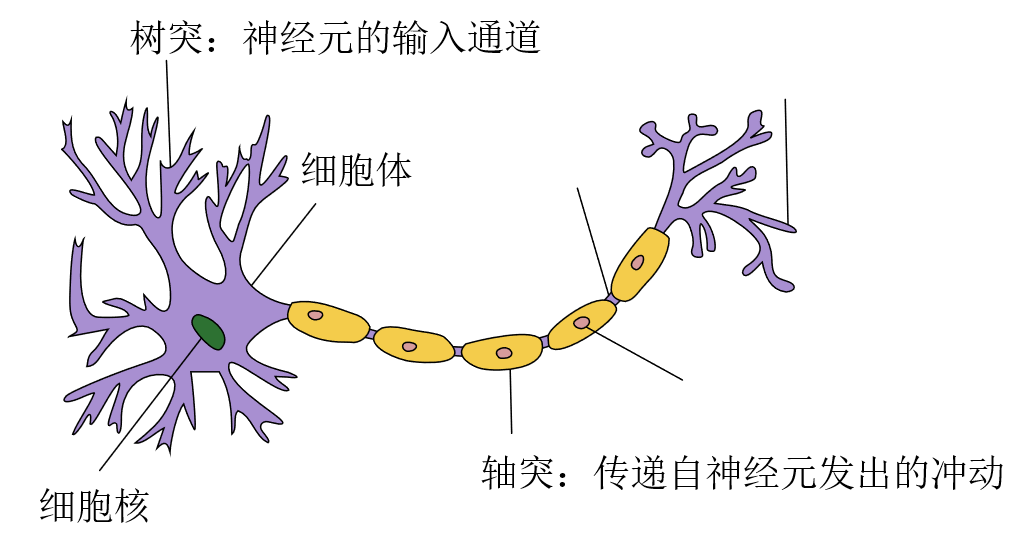
只观察主要部分，我们可以发现生物学上的神经元由三部分组成：细胞体、细胞核、突触。突触可以分为树突和轴突，树突是神经元的输入通道，轴突用于传递自神经元发出的冲动。当神经递质含量满足要求时，神经元便会兴奋、传递冲动。

对生物学上的神经元进行简单的抽象，便得到了M-P神经元模型。

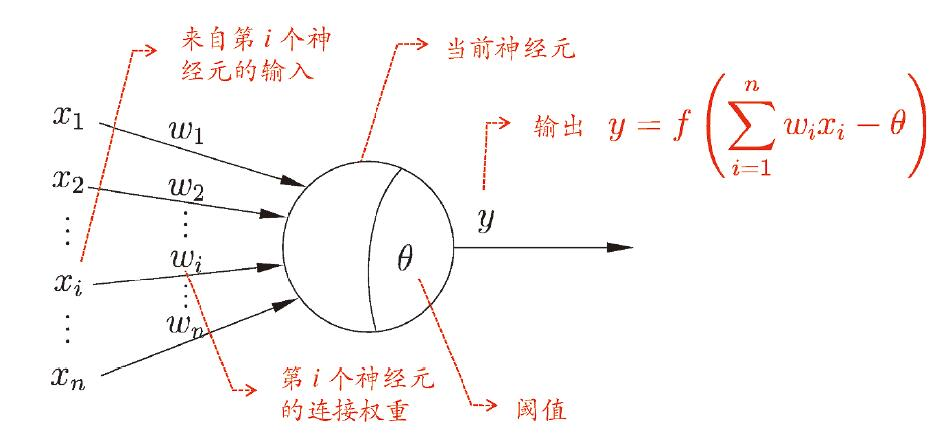
在这个模型中，神经元按权重接收来自其他 $n$ 个神经元传递的输入信号，这些总输入值与神经元的阈值进行比较后，通过“激活函数”处理以产生输出，即。 $y=f(\sum\limits_{i=1}^{n}w_ix_i-\theta)=f(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}-\theta)$

如何选定激活函数呢？典型的激活函数有以下两种：

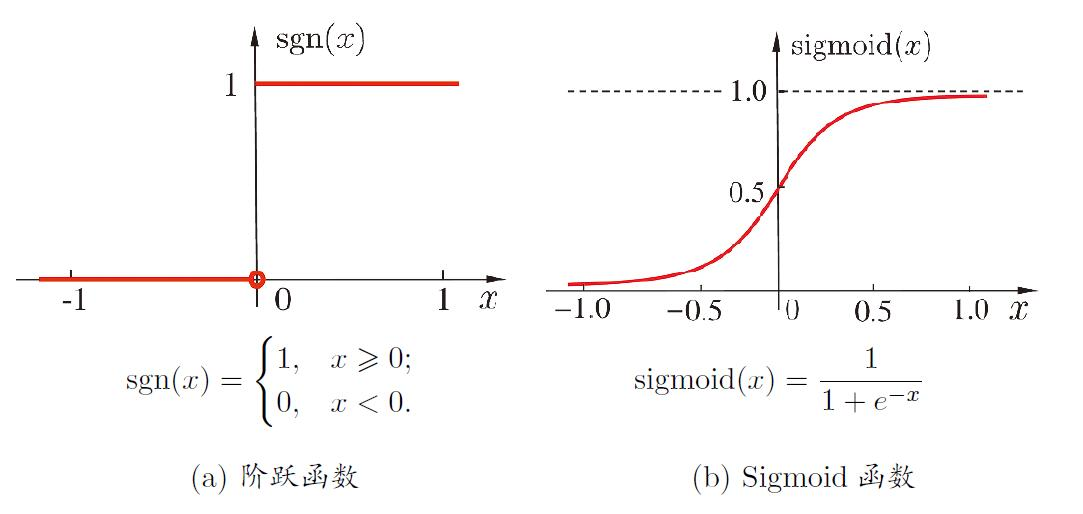
因阶跃函数具有不连续、不平滑的特性，因此常采用$S$型函数，$Sigmoid$函数是最常用的$S$型函数，需要神经元的输出区间为$[-1,1]$时，$S$型函数可以选为双曲正切函数

$f(x)=\frac{1-e^{-\alpha x}}{1+e^{-\alpha x}}$

$Sigmoid$函数也存在缺点，当输入的绝对值大于某个阈值时会过快进入饱和状态，使梯度趋于0，模型收敛缓慢。

$ReLU$函数在一些现代神经网络中也很常用，它是一个很简单的分段线性函数

$f(x)=\left\{ \begin{aligned} & 0 &,x<0\\ & x &,x\geq 0\\ \end{aligned} \right.$

尽管形式简单，但其在卷积神经网络中效果很好。

感知机与多层网络

感知机（Perceptron）：两层神经元，用于实现“与”、“或”、“非”运算。

注意：感知机不能实现异或运算！

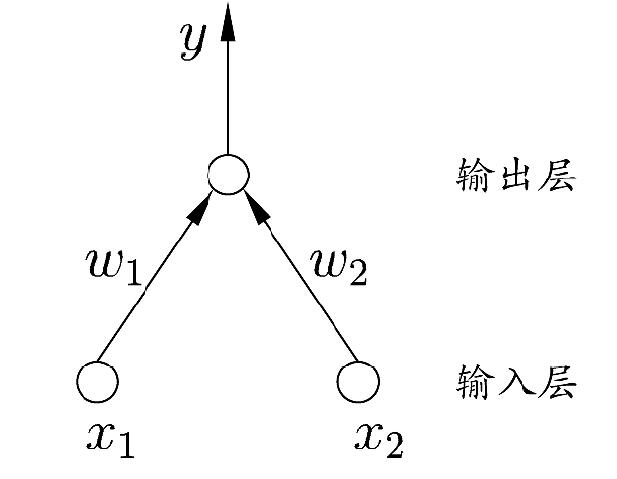
对于上图所示的感知机，选用阶跃函数，有：

$y=\operatorname{sgn}(\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x}-\theta)=\left\{\begin{array}{rcl} 1,& {\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x} -\theta\geq 0}\\ 0,& {\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x} -\theta < 0}\\ \end{array} \right.$

对二维空间进行简单划分即可分别得到与、或、非运算的激活函数，他们不是唯一的。

$x_1$	$x_2$	$y=f(1⋅x_1+1⋅x_2-2)$	$y=f(1⋅x_1+1⋅x_2-0.5)$	$y=f(-0.6⋅x_1+0⋅x_2+0.5)$
0	0	0	0	1
0	1	0	1	1
1	0	0	1	0
1	1	1	1	0

更一般地，我们可以给定数据集，让神经网络通过学习以确定权重 $\omega_i(i=1,2,\dots,n)$ 和阈值$\theta$。若将阈值$\theta$视作固定输入为$-1.0$的哑结点所对应的连接权重$\omega_{n+1}$，则可将权重 $\omega_i(i=1,2,\dots,n)$ 和阈值$\theta$的学习统一为权重 $\omega_i(i=1,2,\dots,n+1)$ 的学习。

$\begin{aligned} \boldsymbol{w}^\mathrm{T}\boldsymbol{x_i}-\theta&=\sum \limits_{j=1}^n w_jx_j+x_{n+1}\cdot w_{n+1}\\ &=\sum \limits_{j=1}^{n+1}w_jx_j\\ &=\boldsymbol{w}^{\mathrm{T}}\boldsymbol{x_i} \end{aligned}$

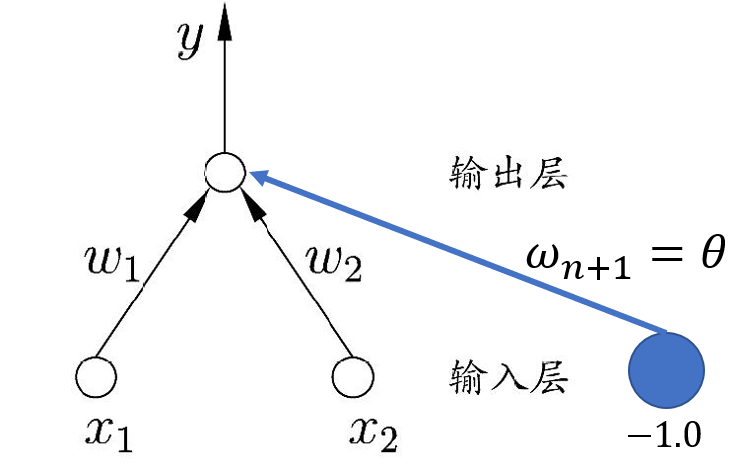
感知机的学习规则为：

$\omega_i\ \gets\ \omega_i + \mathrm{\Delta}\omega_i,\ \mathrm{\Delta}\omega_i = \eta\left(y\ -\ \hat{y}\right)x_i$

其中 $\eta \in (0,1)$，称为学习率，属于超参数。

学习过程很简单：若感知机对训练样例 $(\boldsymbol x,y)$ 中 $\boldsymbol x$ 预测的结果 $\hat{y}$ 等于 $y$ ，则感知机不发生变化。否则，感知机根据错误的程度（残差）进行权重调整。

接下来说明一下为什么两层神经元的感知机不能实现异或运算。首先来看一下与、或、非、异或在二维空间中应怎样被划分。

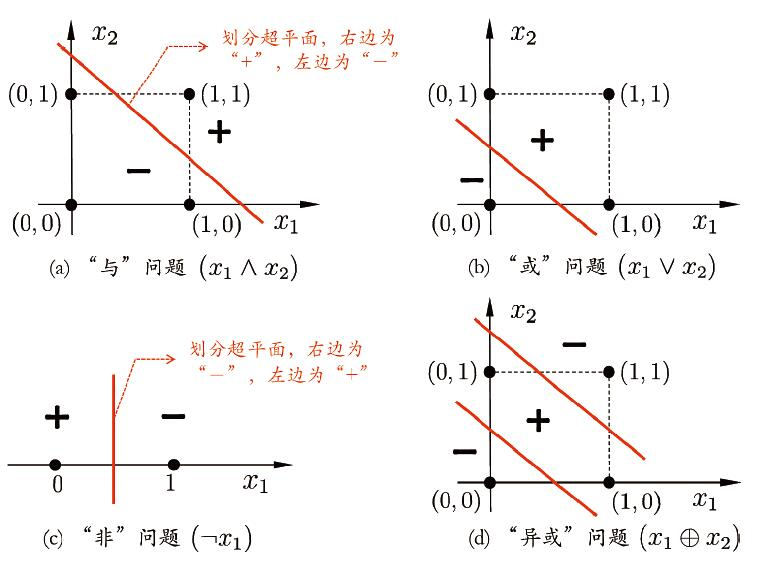
显然，异或问题需要两条直线才能将平面划分为两类模式，而与、或、非只需要一条直线即可。

对于一个有两类模式的空间，若存在一个超平面（$n$ 维欧氏空间中维度等于 $n-1$ 的线性子空间，eg. 平面中的直线）能将他们分开，则称这两类模式是线性可分的。若两类模式是线性可分的，则感知机的学习过程一定会收敛，得到权向量 $\boldsymbol \omega=(\omega_1;\omega_2;\dots;\omega_{n+1})$ .否则感知机会发生振荡，无法求得合适解。

要解决线性可分问题，需要使用多层神经网络。对于异或问题，我们只需要先对与、或问题中的直线使用线性规划

$\left\{ \begin{aligned} x_1+x_2-0.5\geq0 \\ x_1+x_2-1.5\leq0 \\ \end{aligned} \right.$

由简单的谓词逻辑：$P\oplus Q = \neg (P \wedge Q) \wedge (P \vee Q) $，接着对$y^{(1)}=f(x_1+x_2-0.5)$和$y^{(2)}=f(-x_1-x_2+1.5)$使用与问题的激活函数即可。

$x_1$	$x_2$	$y^{(1)}=f(x_1+x_2-0.5)$	$y^{(2)}=f(-x_1-x_2+1.5)$	$y=y^{(1)}+y^{(2)}-1.5$
0	0	0	1	0
0	1	1	1	1
1	0	1	1	1
1	1	1	0	0

最终得到二层感知机如下，输入层与输出层之间的其他神经元层称作隐层。

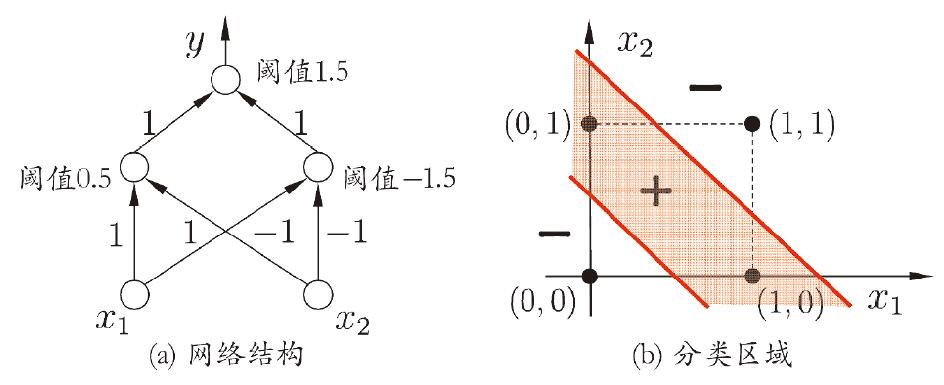
更一般地，常见的神经网络形如：

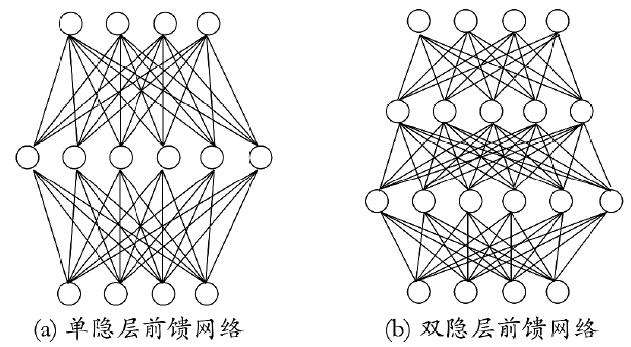
多层前馈神经网络（multi-layer feedforward neural networks）：仅在相邻层间全互连、且包含隐含层的神经网络

注：“前馈”并不意味着网络中信号不能向后传，而是指网络拓扑结构上不存在环或回路。

误差反向传播算法

欲训练一个多层前馈神经网络，我们需要更强大的算法，这其中最成功的神经网络算法即为误差反向传播算法（BackPropagation, BP ），而且它不仅可用于训练多层前馈神经网络，还可用于其他神经网络。通常，“BP网络”指使用BP算法训练的多层前馈神经网络。

下面我们来推导一下BP算法。

首先，给出训练集$D=\{(\boldsymbol x_1, \boldsymbol y_1 ), (\boldsymbol x_2, \boldsymbol y_2 ), …, (\boldsymbol x_m, \boldsymbol y_m )\}, \boldsymbol x_i∈\mathbb{R}^d, \boldsymbol y_i∈\mathbb{R}^l$

给出如下多层前馈神经网络

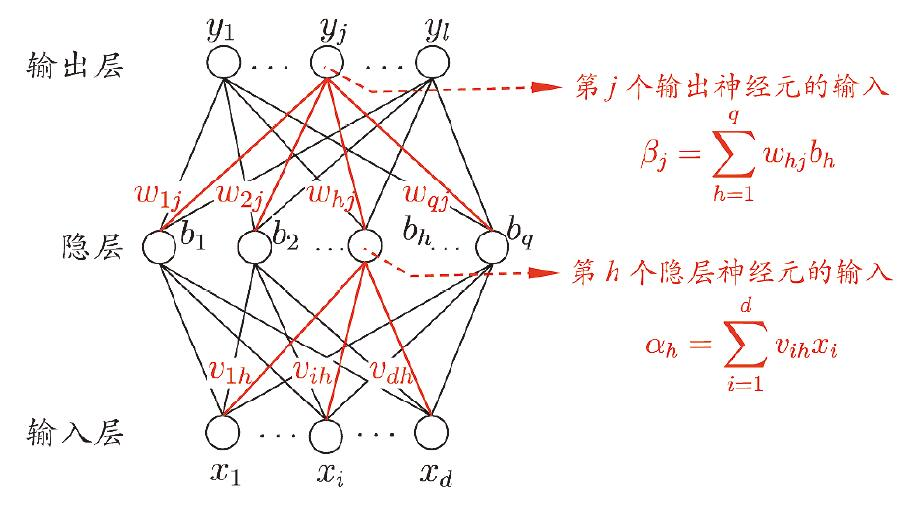
其变量意义标注如下表。

变量	意义
$d$	输入神经元个数
$l$	输出神经元个数
$q$	隐层神经元个数
$\theta_j$	输出层第$j$个神经元的阈值
$γ_h$	隐层第$j$个神经元的阈值
$v_{ih}$	输出层第$i$个神经元与隐层第$h$个神经元间的连接权
$ω_{hj}$	隐层第$h$个神经元与输出层第$j$神经元间的连接权
$\alpha_h$	隐层第$h$个神经元接收到的输入
$\beta_j$	输出层第$j$个神经元接收到的输入
$b_h$	隐层第$h$个神经元的输出

设其隐层和输出层神经元使用$Sigmoid$函数。

对训练例$(\boldsymbol x_k, \boldsymbol y_k )$，假定神经网络的输出为$y ̂_k=(y ̂_1^k,y ̂_2^k,…,y ̂_l^k)$，其中$y ̂_j^k=f(β_j-θ_j)$，

则网络在$(\boldsymbol x_k, \boldsymbol y_k )$上的均方误差为：

$E_k=\frac{1}{2} \sum_{j=1}^{l}(\hat{y}_1^k-y_1^k )^2$

需要确定的参数：

输入层到隐层的$d×q$个权值
隐层到输出层的$q×l$个权值
隐层神经元的$q$个阈值
输出层神经元的$l$个阈值

共$d×q+q×l+q+l=(d+l+1)×q+l$个

广义感知机学习规则：任意参数$v$的更新估计式

$v←v+\Delta v$

对于参数$\omega_{hj}$，以目标的负梯度方向对其进行调整：

$\Delta \omega_{hj}=-\eta\frac{\partial E_k}{\partial \omega_{hj}}$

其中

$\frac{\partial E_k}{\partial \omega_{hj}}=\frac{\partial E_k}{\partial \hat{y}_j^k}\cdot\frac{\partial \hat{y}_j^k}{\partial \beta_j}\cdot\frac{\partial \beta_j}{\partial \omega_{hj}}$

由$\beta_j$的定义，有：

$\frac{\partial \beta_j}{\partial \omega_{hj}}=b_h$

$Sigmoid$的导函数：

$f^{'}(x)=f(x)(1-f(x))$ $\begin{aligned} g_j&=-\frac{\partial {E_k}}{\partial{\hat{y}_j^k}} \cdot \frac{\partial{\hat{y}_j^k}}{\partial{\beta_j}} \\&=-( \hat{y}_j^k-y_j^k ) f ^{\prime} (\beta_j-\theta_j) \\&=\hat{y}_j^k(1-\hat{y}_j^k)(y_j^k-\hat{y}_j^k) \end{aligned}$

所以

$\Delta \omega_{hj}=\eta g_j b_h$

对于参数$\theta_j$：

$\Delta \theta_j = -\eta g_j$

因为

$\Delta \theta_j = -\eta \cfrac{\partial E_k}{\partial \theta_j}$

又

$\begin{aligned} \cfrac{\partial E_k}{\partial \theta_j} &= \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot\cfrac{\partial \hat{y}_j^k}{\partial \theta_j} \\ &= \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot\cfrac{\partial [f(\beta_j-\theta_j)]}{\partial \theta_j} \\ &=\cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot f^{\prime}(\beta_j-\theta_j) \times (-1) \\ &=\cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot f\left(\beta_{j}-\theta_{j}\right)\times\left[1-f\left(\beta_{j}-\theta_{j}\right)\right] \times (-1) \\ &=\cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \hat{y}_j^k\left(1-\hat{y}_j^k\right) \times (-1) \\ &=\cfrac{\partial\left[ \cfrac{1}{2} \sum\limits_{j=1}^{l}\left(\hat{y}_{j}^{k}-y_{j}^{k}\right)^{2}\right]}{\partial \hat{y}_{j}^{k}} \cdot \hat{y}_j^k\left(1-\hat{y}_j^k\right) \times (-1) \\ &=\cfrac{1}{2}\times 2(\hat{y}_j^k-y_j^k)\times 1 \cdot\hat{y}_j^k\left(1-\hat{y}_j^k\right) \times (-1) \\ &=(y_j^k-\hat{y}_j^k)\hat{y}_j^k\left(1-\hat{y}_j^k\right) \\ &= g_j \end{aligned}$

所以

$\Delta \theta_j = -\eta \cfrac{\partial E_k}{\partial \theta_j}=-\eta g_j$

对于参数$v_{ih}$：

$\Delta v_{ih} = \eta e_h x_i$

因为

$\Delta v_{ih} = -\eta \cfrac{\partial E_k}{\partial v_{ih}}$

又

$\begin{aligned} \cfrac{\partial E_k}{\partial v_{ih}} &= \sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \cfrac{\partial \beta_j}{\partial b_h} \cdot \cfrac{\partial b_h}{\partial \alpha_h} \cdot \cfrac{\partial \alpha_h}{\partial v_{ih}} \\ &= \sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \cfrac{\partial \beta_j}{\partial b_h} \cdot \cfrac{\partial b_h}{\partial \alpha_h} \cdot x_i \\ &= \sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \cfrac{\partial \beta_j}{\partial b_h} \cdot f^{\prime}(\alpha_h-\gamma_h) \cdot x_i \\ &= \sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot w_{hj} \cdot f^{\prime}(\alpha_h-\gamma_h) \cdot x_i \\ &= \sum_{j=1}^{l} (-g_j) \cdot w_{hj} \cdot f^{\prime}(\alpha_h-\gamma_h) \cdot x_i \\ &= -f^{\prime}(\alpha_h-\gamma_h) \cdot \sum_{j=1}^{l} g_j \cdot w_{hj} \cdot x_i\\ &= -b_h(1-b_h) \cdot \sum_{j=1}^{l} g_j \cdot w_{hj} \cdot x_i \\ &= -e_h \cdot x_i \end{aligned}$

所以

$\Delta v_{ih} =-\eta \cfrac{\partial E_k}{\partial v_{ih}} =\eta e_h x_i$

对于$\Delta \gamma_h$

$\Delta \gamma_h= -\eta e_h$

因为

$\Delta \gamma_h = -\eta \cfrac{\partial E_k}{\partial \gamma_h}$

又

$\begin{aligned} \cfrac{\partial E_k}{\partial \gamma_h} &= \sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \cfrac{\partial \beta_j}{\partial b_h} \cdot \cfrac{\partial b_h}{\partial \gamma_h} \\ &= \sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot \cfrac{\partial \beta_j}{\partial b_h} \cdot f^{\prime}(\alpha_h-\gamma_h) \cdot (-1) \\ &= -\sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot w_{hj} \cdot f^{\prime}(\alpha_h-\gamma_h)\\ &= -\sum_{j=1}^{l} \cfrac{\partial E_k}{\partial \hat{y}_j^k} \cdot \cfrac{\partial \hat{y}_j^k}{\partial \beta_j} \cdot w_{hj} \cdot b_h(1-b_h)\\ &= \sum_{j=1}^{l}g_j\cdot w_{hj} \cdot b_h(1-b_h)\\ &=e_h \end{aligned}$

所以

$\Delta \gamma_h=-\eta\cfrac{\partial E_k}{\partial \gamma_h} = -\eta e_h$

综上：

$\left\{ \begin{aligned} & \Delta \omega_{hj}=\eta g_j b_h \\ & \Delta \theta_j = -\eta \cfrac{\partial E_k}{\partial \theta_j}=-\eta g_j \\ & \Delta v_{ih} = \eta e_h x_i \\ & \Delta \gamma_h= -\eta e_h \\ \end{aligned} \right. \\ e_h=b_h(1-b_h)\sum_{j=1}^l w_{hj}g_j$

需要精细调节时，可令(1)与(2)使用$\eta_1$，(3)与(4)使用$\eta_2$

由此，我们可以给出标准BP算法：

值得注意的是，BP算法的最终目标应为最小化训练集$D$上的累计误差

$E=\frac{1}{m} \sum_{k=1}^mE_k$

但刚才的标准BP算法基于最小化均方误差$E_k$推导。

累计误差反向传播算法

标准BP算法由单个均方误差$E_k$推导而来，所以每次更新针对单个样例，更新频繁。

同时，同一数据集中不同样例的反向更新可能出现“抵消”现象。

若类似地，对之前最终目标中提到的累积误差推导更新规则，便得到了更新频率更低的累计误差反向传播算法。

标准 BP 算法

$E_k=\frac{1}{2} \sum_{j=1}^{l}(\hat{y}_1^k-y_1^k )^2$

每次针对单个训练样例更新权值与阈值
参数更新频繁，不同样例可能抵消，需要多次迭代

累计BP算法

$E=\frac{1}{m} \sum_{k=1}^mE_k =\frac{1}{2m} \sum_{k=1}^m\sum_{j=1}^l(\hat{y}_1^k-y_1^k)^2$

其优化目标是最小化整个训练集上的累计误差
读取整个训练集一遍才对参数进行更新 , 参数更新

过拟合

BP网络经常出现过拟合现象。

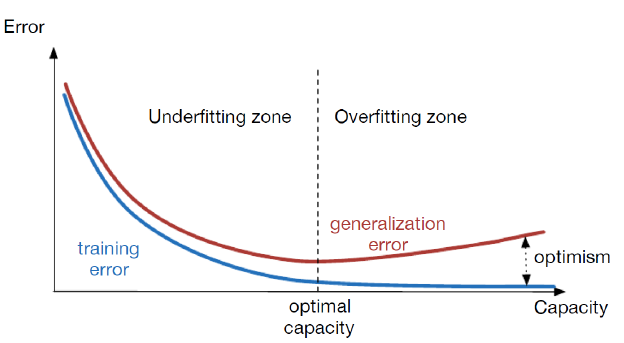
过拟合（overfitting）：训练误差持续降低，测试误差上升。即model对训练集性能很好，对测试集性能很差，也就是model的generalization差。

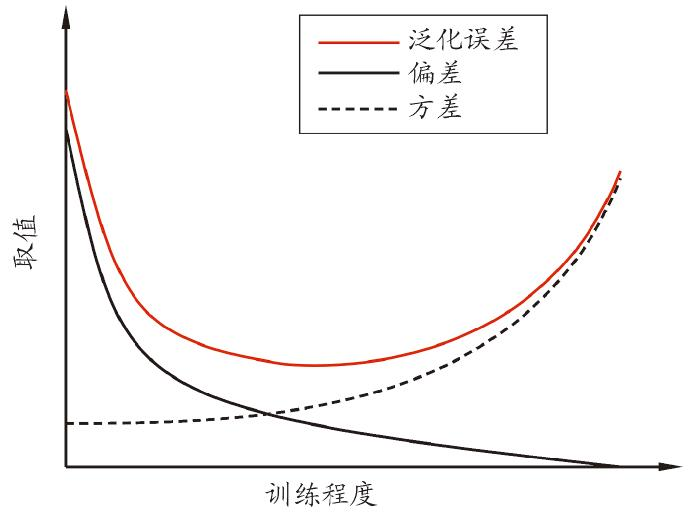
偏差–方差窘境：

缓解过拟合现象有几种策略：

确保训练数据集和测试数据集是independent, identical distributed(i.i.d)的；
早停（ early stopping ）：若训练集误差降低，但验证集误差升高，则停止训练；
正则化（ regularization ）：在误差目标函数中增加一个用于描述网络复杂度的部分。例如：

$E=\lambda\frac{1}{m} \sum_{k=1}^mE_k +(1-\lambda)\sum_i{\omega_i^2}$

全局最小与局部最小

局部极小：对 $\forall(\boldsymbol \omega;\theta)\in \left\{∀(\boldsymbol \omega;\theta)\ |\ ‖(\boldsymbol \omega;\theta)-(\boldsymbol \omega^∗;\theta^∗)‖ ≤ \epsilon\right\}$ ，都有 $E(\boldsymbol \omega;\theta)\geq E (\boldsymbol \omega^∗;\theta^∗)$ ，则 $(\boldsymbol \omega^∗;\theta^∗ )$ 为局部极小解。即梯度为$0$且$E$小于某个邻点。

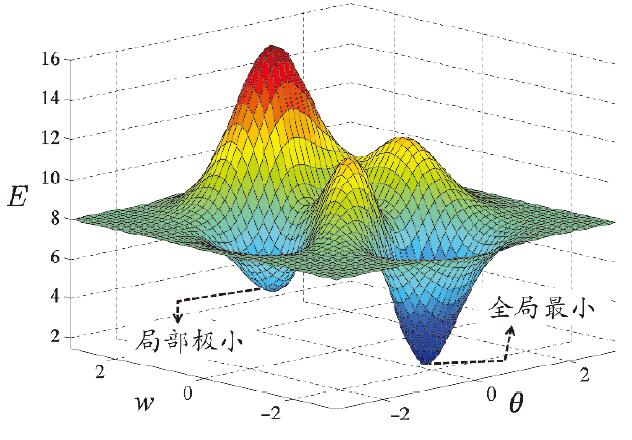
全局极小：对 $\forall(\boldsymbol \omega;\theta)$ ，都有 $E(\boldsymbol \omega;\theta)\geq E (\boldsymbol \omega^∗;\theta^∗)$ 则 $(\boldsymbol \omega^∗;\theta^∗ )$ 为全局极小解。

因为BP算法的感知机更新规则基于梯度下降，所以当误差函数有多个局部极小时，则不能找到全局极小解，此时我们称参数寻优陷入了局部极小。

“跳出”局部极小的常见策略：

不同的初始参数
模拟退火
随机扰动
遗传算法
……