Mu Li. Dive into Deep Learning

课程地址：https://courses.d2l.ai/zh-v2/

课程回放：https://b23.tv/Fc52WcK

教材地址：https://zh-v2.d2l.ai/

教材讨论：https://discuss.d2l.ai/

Preliminaries

线性代数

Frobenius Norm，将矩阵拉成向量，求向量长度。

其他的一般不用。

generalizes to：v. 推广为

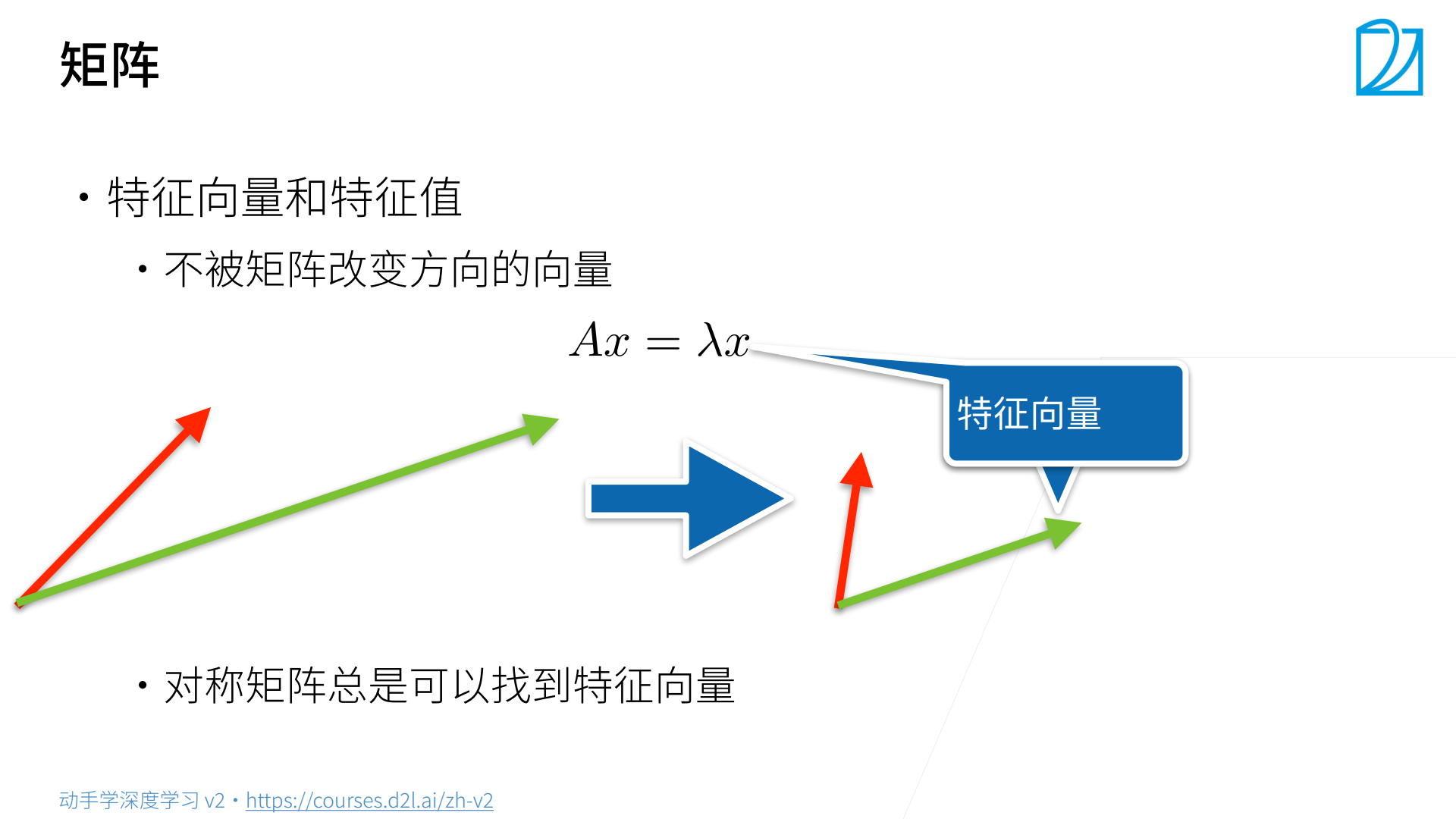
矩阵作用于特征向量时，特征向量方向不变。

按轴求和

什么是按轴求和、降低维度？

给你一张染了色的纸，把它竖着或横着挤压成一个棍，这就是降维；它的颜色会变深，这就是求和。

pytorch中用于按轴求和的方法是torch.Tensor.sum，其调用torch.sum函数

pytorch docs给出的说明

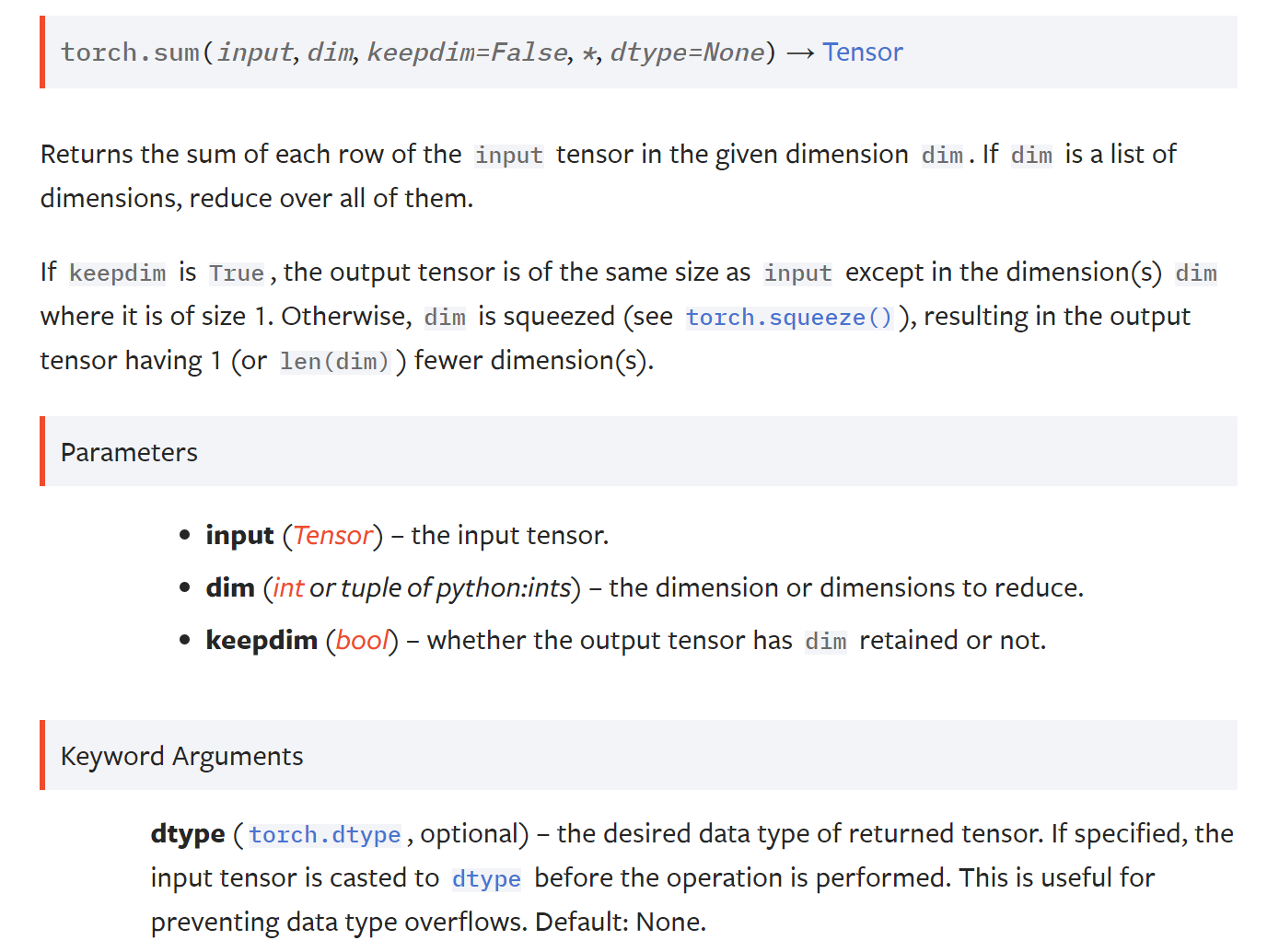
返回输入张量input在给定维度dim上每行的和，如果dim是一个维度的列表，把它们全部降低。

这里的维度是怎么定义的？

以正常遍历的维度作为维度0，每往里1层，其维度比上一层多1。

比如这里有一个二维的tensor（三种常见的创建方式）

其正常的遍历for i in A，每个i都是一个一维tensor，这个维度就是dim 0。

在这个维度上求和，即把每个i相加，其大致流程为

类似地，在dim 1上求和

如果keepdim为True，那么输出tensor和输入tensor具有相同的维度数量（维数），但被降维的那些维度大小为1。

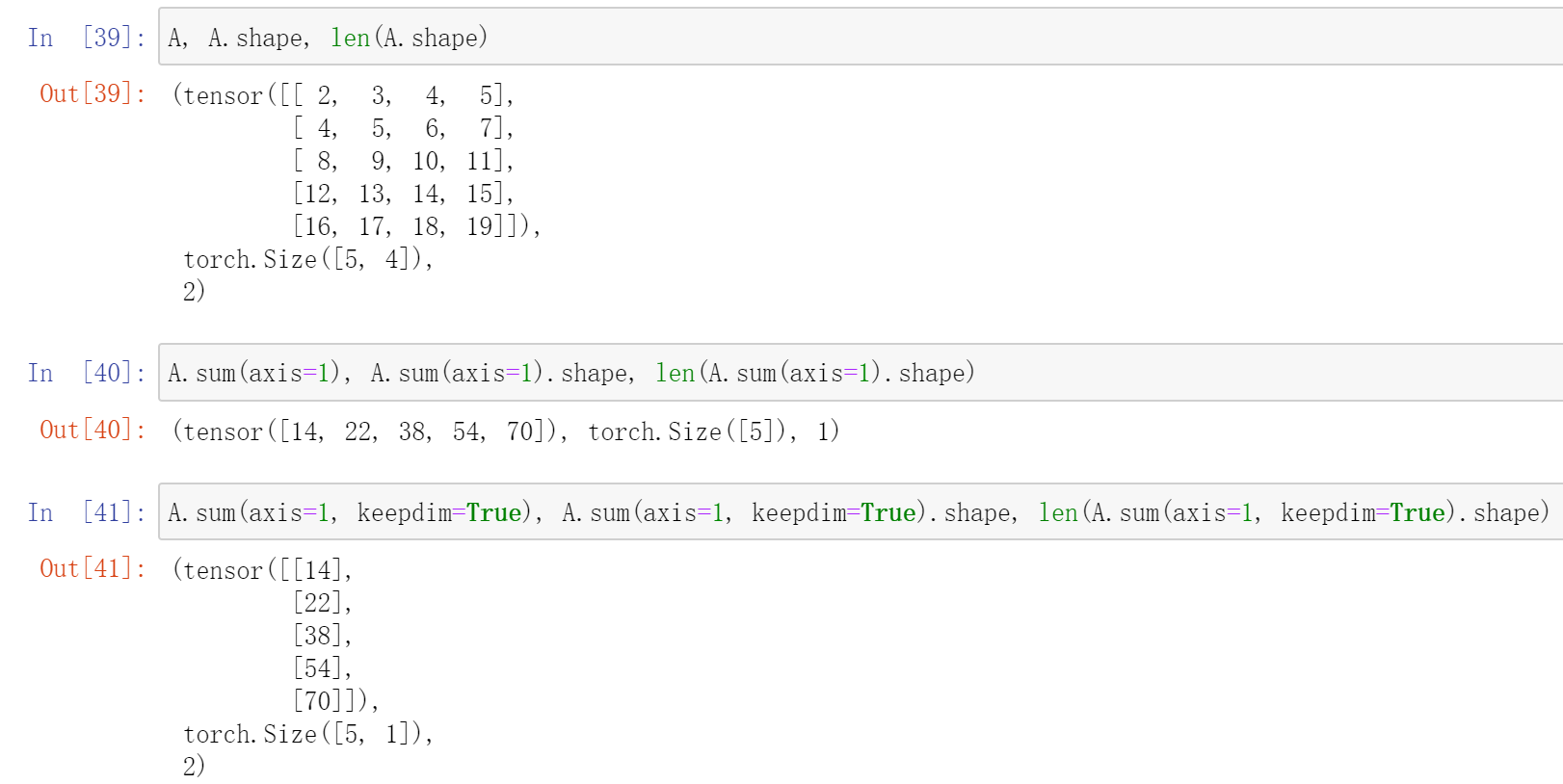
保持相同的维数有什么用？

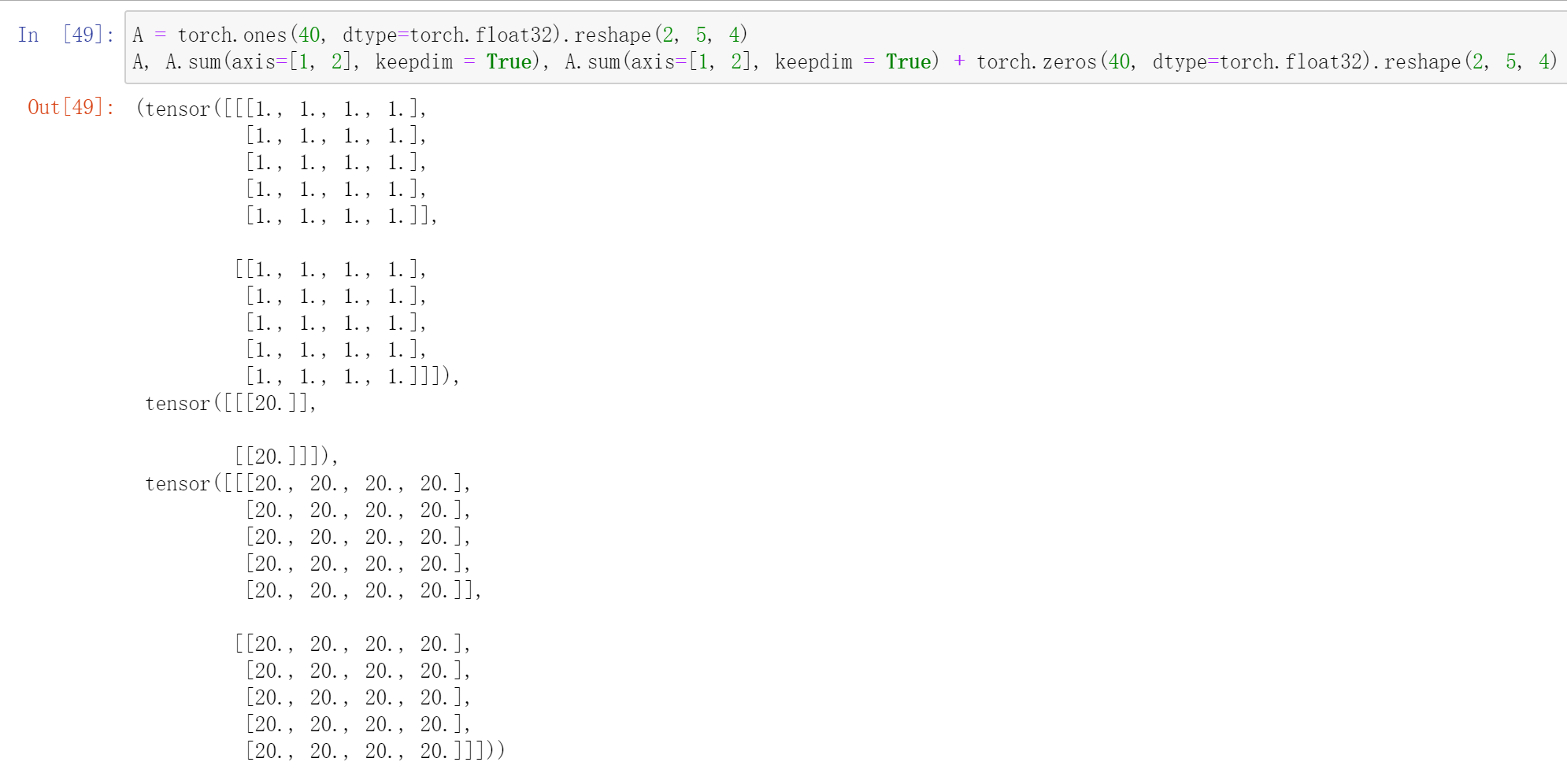
广播。

广播就是当两个tensor相加时，如果shape不相同，但维数相同且有些维度的数量为1，可以复制这些维度上的小tensor，使其shape在这个维度上的数量与较大者相等。

Linear Networks

线性回归

QA

Q：损失为什么要求平均？

A：除以n的好处是，不论批量多大，梯度的值都差不多（都是平均值），与学习率$\eta$解耦。

---

Q：batchsize是否会影响模型结果？

A：事实上，batchsize越小，模型结果越好，这一点比较反直觉。因为SGD理论上是给模型带来噪音，batchsize越小，噪音越大，但噪音对神经网络是一件好事，因为深度神经网络比较复杂，有噪音可以不容易“跑偏”，更鲁棒，泛化能力更强。

---

Q：随机梯度下降中的随机？

A：随机，指的是元素是随机的，即随机采样。

---

Q：为什么机器学习优化算法采用梯度下降这种一阶导算法，而不采用收敛更快的牛顿法等二阶导算法？

A：首先牛顿法用不了，只能用近似的牛顿法。机器学习中有两个模型，统计模型（Loss）、优化模型（Optim），这两个东西都是错的（可能是想说和现实规则不一样？），所以我们不关心收敛速度，而关心收敛到什么地方，是否泛化能力更强。

---

Q：detach的作用？

A：将其从计算图中剥离，不再计算其梯度，某些pytorch需要先进行这步操作再转为numpy。

---

Q：样本大小不是batchsize的整数倍怎么办？

A：做法一：剩下多少就拿多少，做法二：丢弃，做法三：从下一个epoch补缺少的的过来

Softmax 回归

Softmax回归中exp的作用是将输入域映射到$(0, +\inf)$，其本质上是将预测的值转为概率，分类问题给出的标签本就是一种概率，衡量两个概率间的区别使用交叉熵（CE）

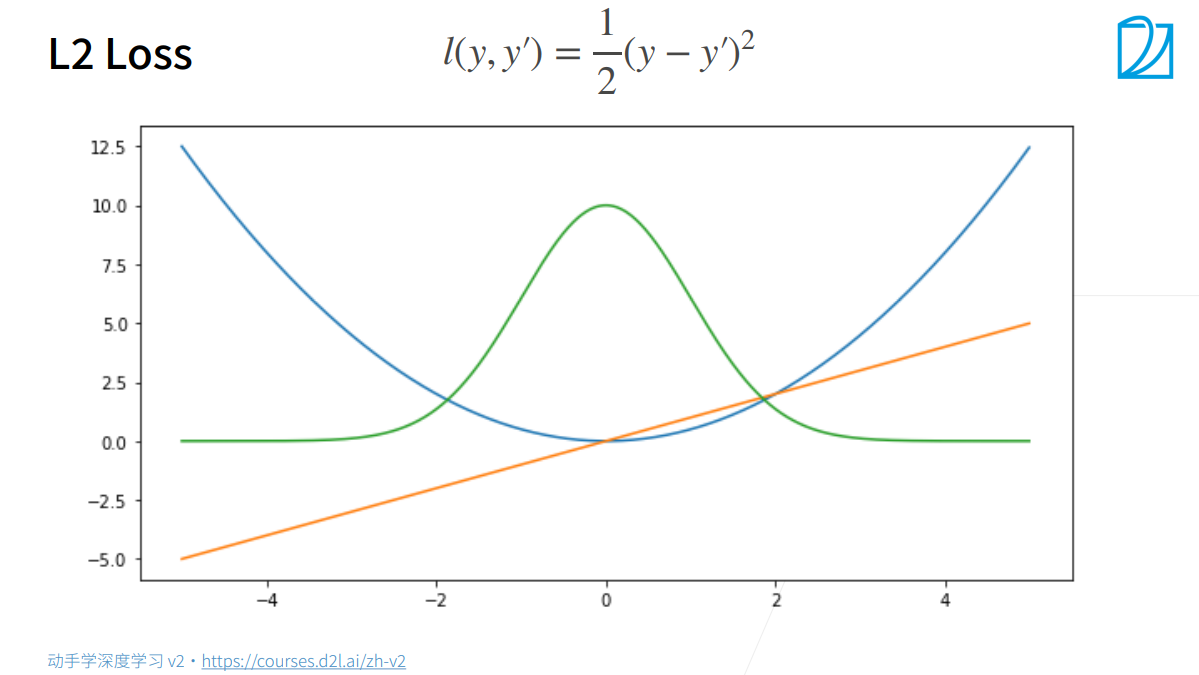
蓝：$l$

绿：$l$的似然函数

橙：$l$的梯度

L2 Loss

L1 Loss

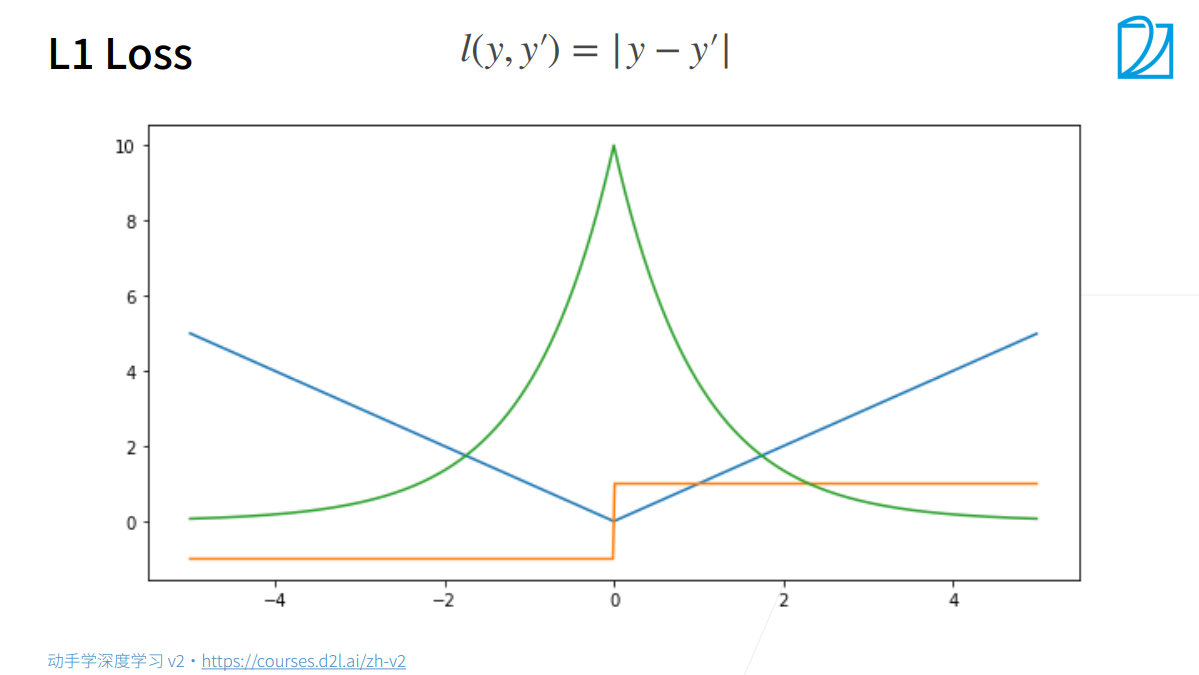
当预测值与真实值较远时，梯度永远是常数，权重更新不会太大，更稳定；

当预测值与真实值较近时，因为sub gradient是[-1, 1]间的任意值，在优化末期时不稳定。

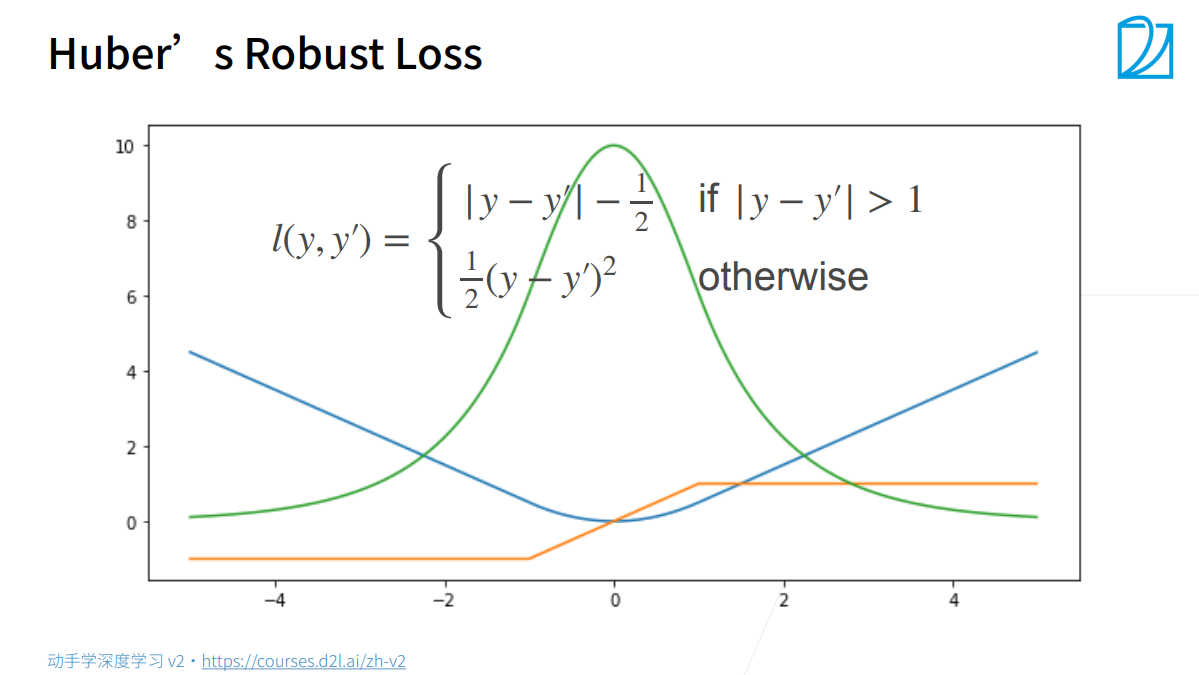
Huber’s Robust Loss

L1和L2的缝合形式，避免L1的间断点

$$l(y, y^{\prime}) = \begin{cases} \left\vert y - y^{\prime}\right\vert - \frac{1}{2} & if \left\vert y - y^{\prime}\right\vert > 1\\ \frac{1}{2}\left(y - y^{\prime}\right)^2 & otherwise \end{cases}$$

QA

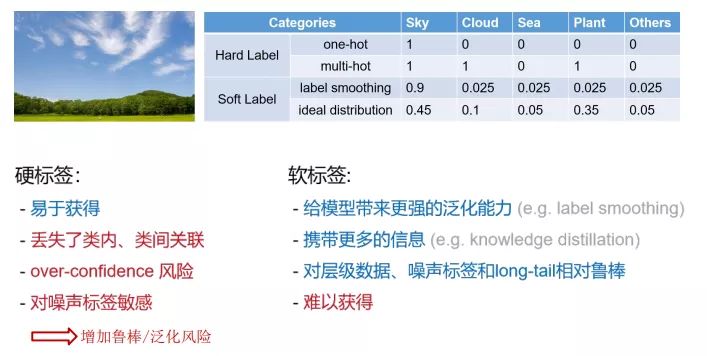
Q：soft label？

A：softmax回归很难用指数逼近0或1这种极端数值，所以将正确的类记为$0.9$，不正确的类记为$\frac{0.1}{n-1}$。

更多：从Label Smoothing和Knowledge Distillation理解Soft Label（陀飞轮）

---

Q：batchsize的大小为什么没有影响训练速度？

A：batchsize不影响计算量，只影响并行度，进而影响执行的效率。不影响的原因可能是模型很小或是在CPU上训练。

---

Q：测试时为什么要设net.eval()？

A：将网络设置为评估模式后，pytorch不会计算梯度，进而不会计算与梯度相关的操作，可以提升效率、不影响训练过程。

---

Q：optimizer是怎么获取Model的参数的？

A：初始化时传递的，optimizer = torch.optim.SGD(net.parameters(), lr=0.1)

MultiLayer Perceptrons

感知机

QA

Q：单层神经网络有万有逼近性，为什么神经网络趋向于增加隐藏层的层数（深度）而不是神经元的个数（宽度）？

A：理论上，单层感知机具有万有逼近性，可以拟合任何函数；实际上，优化算法解不了。

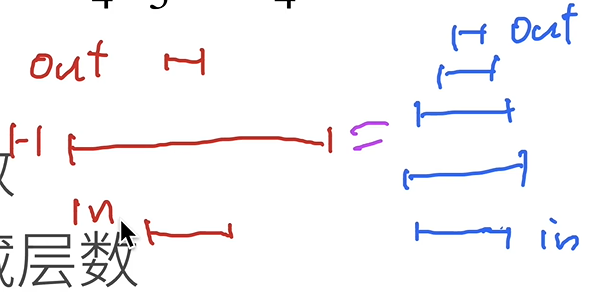
两种神经网络，左侧为“浅度学习”的神经网络，右侧为深度学习的神经网络。理论上，二者的拟合能力相同；但实际上，左侧的网络特别容易overfitting，因为所有神经元都是并行的，不容易迭代到理论解。

直观的例子：

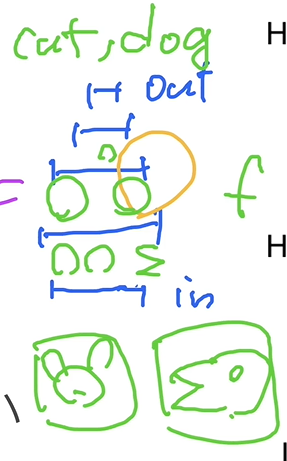
让每层学出部分特征，如第一层学个耳朵/嘴，第二层学个头等等。

过拟合和欠拟合

introduction

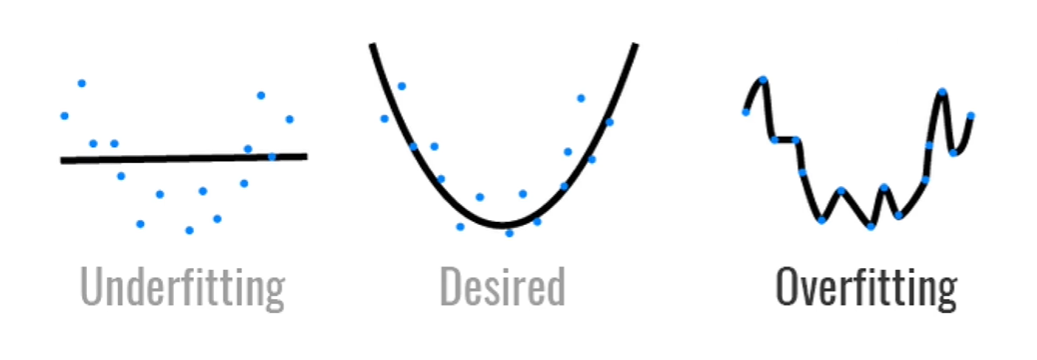
模型容量：参数数量+参数值的范围

理论依据：VC维，在深度学习中很难计算

QA

Q：SVM相对于神经网络的缺点

A：1. SVM使用kernel，很难达到百万级

1. 可调整的参数少
2. 神经网络更灵活，可编程性强

---

Q：K折交叉验证在深度学习中是否常用？

A：K折交叉验证确实在深度学习中用的不多。K折交叉验证主要解决机器学习中数据集太小的情况，深度学习的数据集很大，所以很少用。

权重衰减

introduction

一种处理过拟合的方法

模型过拟合，是因为其复杂度太高，即模型容量太大，所以我们有两种方法处理过拟合。

1. 减少参数数量
2. 限制参数值的范围，如$|\boldsymbol{w}|^2 \leq \theta$

在模型结构上做出创新不是一件容易的事，所以我们应该先在现有的模型上找到更优的模型参数。

因此，我们可以使用罚函数法限制模型参数的范围，即

形式化原问题

$$\begin{aligned} \underset{\boldsymbol{w}}{\min}\ &\ell(\boldsymbol{w}, b)\\ \text{s.t.}\ &\|\boldsymbol{w}\|^2 \leq \theta \end{aligned}$$

应用罚函数法

$$\begin{aligned} \underset{\boldsymbol{w}}{\min}\ &\ell(\boldsymbol{w}, b) + \frac{\lambda}{2}\|\boldsymbol{w}\|^2 \end{aligned}$$

反向传播更新参数时

$$\begin{aligned} \frac{\partial}{\partial \boldsymbol{w}}\left(\ell(\boldsymbol{w}, b)+\frac{\lambda}{2}\|\boldsymbol{w}\|^2\right) &= \frac{\partial \ell(\boldsymbol{w}, b)}{\partial \boldsymbol{w}}+\lambda \boldsymbol{w} \\ \boldsymbol{w}_{t+1} &\leftarrow \boldsymbol{w}_{t} - \eta \frac{\partial}{\partial \boldsymbol{w}_t}\left(\ell(\boldsymbol{w}_t, b_t) + \frac{\lambda}{2}\|\boldsymbol{w}_t\|^2\right) \\ \boldsymbol{w}_{t+1} &\leftarrow (1-\eta\lambda)\boldsymbol{w}_t - \eta \frac{\partial \ell(\boldsymbol{w}_t, b_t)}{\partial \boldsymbol{w}_t} \end{aligned}$$

未增加“罚”（penalty）时，权重迭代公式为

$$\boldsymbol{w}_{t+1} \leftarrow \boldsymbol{w}_t - \eta \frac{\partial \ell(\boldsymbol{w}_t, b_t)}{\partial \boldsymbol{w}_t}$$

通常，$\eta\lambda<1$。因此，权重$\boldsymbol{w}_t$在梯度下降前会衰减一次，所以罚函数法在深度学习中就称为权重衰减。

Note. 一般不对$b$做权重衰减，因为效果不大。

QA

Q：为什么限制参数值的范围可以降低复杂度？

A：当参数的范围很大时，可能会出现下图的“陡峭”情况。（想象一下$y=\text{big number}\cdot \sin(x)$的泰勒展开式，次数为1的项和次数为7的项，它们的范围就很大）

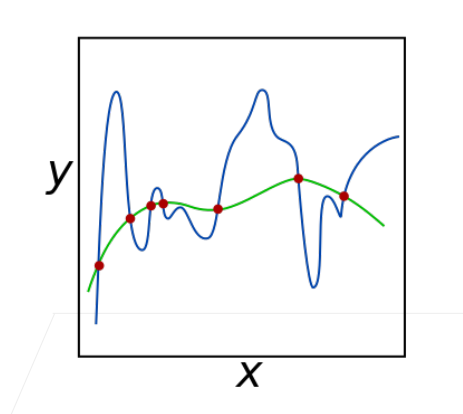
所以限制参数的范围，即限制拟合函数必须“平滑”（类似PhotoShop的钢笔工具，把锚点相互离得很近），所以就减少了复杂性。

---

Q：L2 norm的符号？

A：L2 norm（二范数）的符号应该是$|\boldsymbol{w}|_2$，表示$\sqrt{\sum_{i = 1}^{m}w_i^2}$。所以$|w|_2^2 = \sum_{i = 1}^{m}w_i^2$，即分量的平方和。对于向量来说，二范数就是默认的范数。所以对向量，有$|w|_2 = |w|$，$|w|_2^2 = |w|^2$。

---

Q：假如真正的$\boldsymbol{w}$就是比较大，那加入参数衰减令参数减小，会有反作用吗？

A：因为我们获取到的数据是真实数据的一部分，所以肯定会有噪音，$\lambda$的作用就是处理这些噪音；

假设没有噪音，那么就不会train到奇怪的地方，就不需要参数衰减了；

（我个人觉得是有的，但是与他所对抗噪音带来的好处比，可以忽略它的反作用）

Dropout

motivation

一个好的模型要对输入数据的扰动“鲁棒”。

就像下面这张High School Graduation dropout rate（高中毕业辍学率）一样，淘汰掉一部分输入的学生，可以让输出的结果更优。

process

在层间“无偏差地”加入噪音，等价于对数据进行一个Tikhonov正则。

“无偏差”，即对$\boldsymbol{x}$加入噪音，形成$\boldsymbol{x}^\prime$，使得

$$\mathbb{E}(\boldsymbol{x}^\prime) = \boldsymbol{x}$$

Note. 这里是element-wise相等，不是说“一个期望等于一个向量”，而是说“$x^\prime$的每个元素的期望与$\boldsymbol{x}$的对应元素相等”（重载的等于号）

Dropout对每个元素做如下扰动

$$x_i^{\prime}= \begin{cases} 0 & \text { with probablity } p \\ \frac{x_i}{1-p} & \text { otherise } \end{cases}$$

使得

$$\mathbb{E}(x^\prime_i) = p \times 0 + (1-p) \cdot \frac{x_i}{1-p} = x_i$$

即

$$\mathbb{E}(\boldsymbol{x}^\prime) = \boldsymbol{x}$$

通常在层间使用Dropout，如

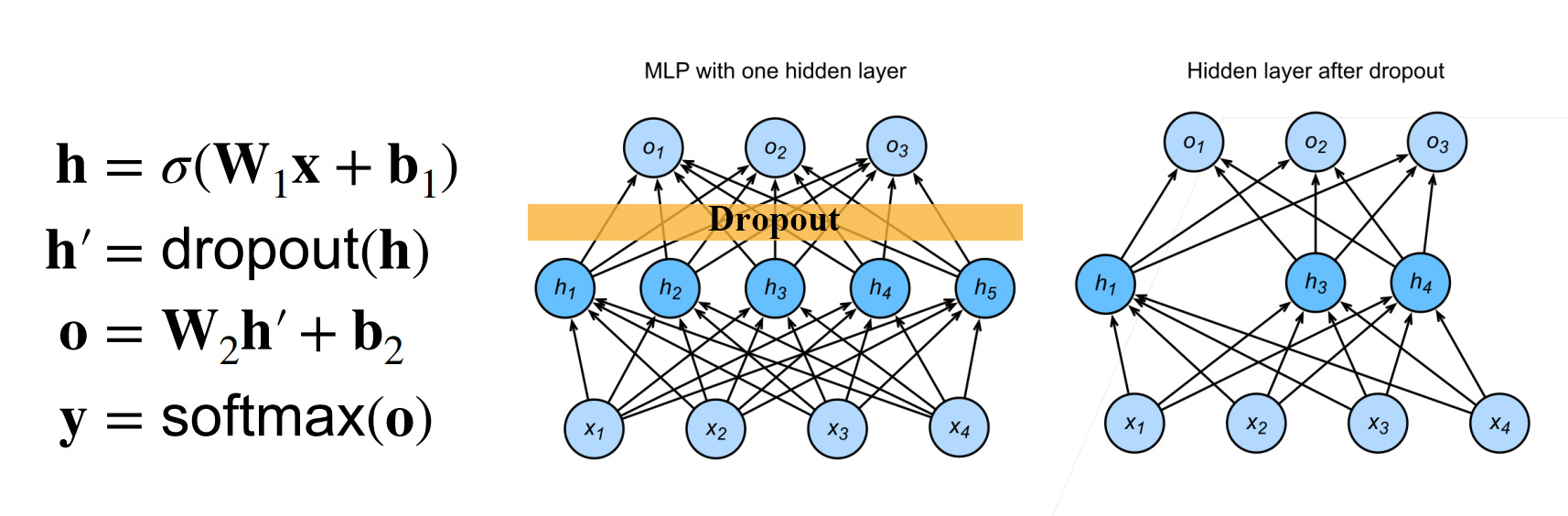
注意.

droupout只在train时生效，使$h \gets \operatorname{dropout}(h)$

在test/inference时关闭，即$h \gets h$，可以保证输出的确定性。

QA

Q：dropout随即丢弃，如何保证结果的正确性、可重复性？

A：首先，机器学习没有“正确性”，只有“准确性”。

神经网络的“可重复性”一直是一件困难的事情，但可以固定一些参数以减小“随机性”：

1. 固定random seed
2. 固定神经网络的初始权重
3. 禁用NVDIA CUDA中的DNN Library。DNN Library会带来50%~80%的加速，但是受计算机体系结构的限制，并行化导致相加顺序变化，所以每次矩阵运算的结果是不同的，

但是其实没必要保证可重复性，只要精度在一个范围内就行。“随机性”不是一个坏事情，也可以让神经网络更稳定、平滑。如果神经网络在各种随机下仍然能够收敛，那么以后训练时也可以收敛。

---

Q：BN和dropout会同时使用吗？

A：BatchNorm是给卷积层用的，而dropout作用于全连接层，二者没有什么相关性。

---

Q：dropout是否会让loss曲线不平滑？

A：正常情况下，如果每个batch后都计算一次loss的话，是平滑的，但这样很“贵”，所以一般都是10个batch后计算一次loss并作图，这时可能是不平滑的。但我们对loss曲线不care，不平滑就不平滑，因为曲线的最后肯定是平滑的，否则代表无法收敛。

---

Q：dropout每个epoch随机选择子网络，最后做平均。这种做法是不是类似于投票的思想？

A：Geoffrey Hinton最初设计dropout时是这样认为的，但有几篇paper认为”Dropout is a regularization”，大家通过实验认为它更像一个正则项。所以Hinton在2017年提出了Capsule Networks，但是这个网络还没有work。

---

Q：dropout已被Google申请专利，产品开发时可以使用吗？

A：Google不仅申请了dropout，也给RNN和transformer等许多技术申请了专利。我在Amazon用dropout，我们的律师也没有说不可以用，但也没有说可以用。（好搞笑啊哈哈哈哈）

---

Q：dropout和weight decay都属于正则，哪个更常用呢？

A：一般weight decay更常用，dropout主要对全连接层使用，而weight decay对CNN、transformer等都可以使用。weight decay的lambda不太好调参。dropout的probability更好调参，因为它很直观，一般只有三种经验值：0.1、0.5、0.9。

什么时候使用dropout呢？假如有一个单隐层MLP，隐层的大小为64，当没有使用dropout时，训练结果没有那么过拟合。那么接下来就可以尝试大小为128的隐层+dropout(p=0.5)。

总得来说，深度学习是希望模型够强，然后通过正则来保证它不过拟合（学偏）。

回到这个问题，dropout使用的多还是因为比较好调参，例如模型特别大、隐藏层特别复杂，就可以dropout(p=0.9)，丢弃90%层间数据，成为强回归器；反之，则dropout(p=0.1)，成为弱回归器。

---

Q：在同样的lr下，使用dropout是否会使得参数收敛变慢，需要调高lr吗？

A：是有可能减慢收敛的，因为参数梯度更新的更少了。但是没有哪种经验说需要调高lr，因为lr对期望和方差更敏感，而dropout不改变期望。

数值稳定性

introduction

考虑如下的d层神经网络

$$\begin{cases} \boldsymbol{h}^t=f_t\left(\boldsymbol{h}^{t-1}\right) \\ y=\ell \circ f_d \circ \ldots \circ f_1(\boldsymbol{x}) \end{cases}$$

计算损失$\ell$关于参数$\boldsymbol{W}_t$的梯度时，有

$$\begin{aligned} \frac{\partial \ell}{\partial \boldsymbol{W}^t} &=\frac{\partial \ell}{\partial \boldsymbol{h}^d} \frac{\partial \boldsymbol{h}^d}{\partial \boldsymbol{h}^{d-1}} \ldots \frac{\partial \boldsymbol{h}^{t+1}}{\partial \boldsymbol{h}^t} \frac{\partial \boldsymbol{h}^t}{\partial \boldsymbol{W}^t} \\ &=\frac{\partial \ell}{\partial \boldsymbol{h}^d} \cdot \prod_{i=t}^{d-1}\frac{\partial \boldsymbol{h}^{i+1}}{\partial \boldsymbol{h}^{i}} \cdot \frac{\partial \boldsymbol{h}^t}{\partial \boldsymbol{W}^t} \end{aligned}$$

其中，因向量对向量的微分为矩阵，所以需计算包含$d-1-t+1=d-t$次矩阵乘法。

当神经网络的深度增加时，大量的矩阵乘法会带来两个问题：

• 梯度爆炸：如$1.5^{100} \approx 4 \times 10^7$
• 梯度消失，如$0.8^{100} \approx 2 \times 10^{-10}$

example

假如有以下MLP（偏移并入$\boldsymbol{W}$中）

$$\boldsymbol{h}^t=f_t\left(\boldsymbol{h}^{t-1}\right)=\sigma\left(\boldsymbol{W}^t \boldsymbol{h}^{t-1}\right)$$

每层的输出对输入的微分为

$$\frac{\partial \boldsymbol{h}^t}{\partial \boldsymbol{h}^{t-1}} =\operatorname{diag}\left(\sigma^{\prime}\left(\boldsymbol{W}^t \boldsymbol{h}^{t-1}\right)\right)W^t$$

Note. 这里不应该有转置，每层的微分是这样得到的：事实上，按分子布局，有$\frac{\partial A\cdot\boldsymbol{x}}{\partial \boldsymbol{x}}=A$。所以，即使加入sigmoid函数，也应该是一个$m \times n$的矩阵。按嵌套求导规则大概可以得到$\sigma^{\prime}\left(\boldsymbol{W}^t \boldsymbol{h}^{t-1}\right)W^t$，但是这个结果的矩阵布局是$(m \times 1) \times (m \times n)$，不符合求导规则，所以要让前面的向量对角化（这里的$\operatorname{diag}(\cdot)$）以成为成$(m \times m) \times (m \times n)=m \times n$。

$\ell$对$\boldsymbol{W}_t$微分需要的矩阵乘积为

$$\prod_{i=t}^{d-1} \frac{\partial \boldsymbol{h}^{i+1}}{\partial \boldsymbol{h}^i} =\prod_{i=t}^{d-1} \operatorname{diag}\left(\sigma^{\prime}\left(\boldsymbol{W}^i \boldsymbol{h}^{i-1}\right)\right)W^i$$

梯度爆炸

当$\sigma(\cdot)=\operatorname{ReLU}(\cdot)$时

$$\sigma(x)= \begin{cases} x &,x \geq 0 \\ 0 &,\text{otherwise} \end{cases} \\ \sigma^{\prime}(x)= \begin{cases} 1 &,x \geq 0 \\ 0 &,\text{otherwise} \end{cases}$$

$\operatorname{diag}\left(\sigma^{\prime}\left(\boldsymbol{W}^i \boldsymbol{h}^{i-1}\right)\right)$中仅有对角线元素，且为0或1。这时，其与$W^i$相乘，会使$W^i$的某些行清零，其他行保留原来的值（将左边矩阵的每行转置后依次放在右边矩阵的列上，列向量为onehot则保留右侧矩阵的行，列向量为零向量则清零右侧矩阵的行）。这样，$\prod_{i=t}^{d-1} \frac{\partial \boldsymbol{h}^{i+1}}{\partial \boldsymbol{h}^i}$中的一些元素会来自$\prod_{i=t}^{d-1}W^i$。当网络加深时，$d-t$就会很大，如果$W^i$中的元素大于1，累乘会使最终结果很大，即梯度爆炸。

梯度爆炸带来的问题

• 累乘值会超出值域（当超过值域时成为infinity）

  • 对16位浮点数（float16，半精度浮点数）尤为严重

    

    可见，最小正规数（下溢阈值）$\approx 6e-5$，最大值$\approx6e4$，数值区间很小。

• 对学习率敏感

  • 学习率太大$\to$大参数值$\to$更大的梯度
  • 学习率太小$\to$训练无进展
  • 需要在训练过程动态调整学习率

梯度消失

当$\sigma(\cdot)=\operatorname{logistic}(\cdot)$时

$$\begin{aligned} \sigma(x) &= \frac{1}{1+\exp(-x)} \\ \sigma^{\prime}(x) &= \sigma(x)(1-\sigma(x)) \end{aligned}$$

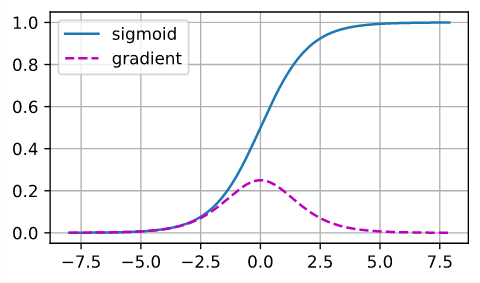
当输入值很大时，激活函数的梯度值很小，即$\operatorname{diag}\left(\sigma^{\prime}\left(\boldsymbol{W}^i \boldsymbol{h}^{i-1}\right)\right)$中仅有对角线元素，且值很小。当网络加深时，$d-t$就会很大，如果$\boldsymbol{W}^i \boldsymbol{h}^{i-1}$的每个元素很大，$\sigma^{\prime}\left(\boldsymbol{W}^i \boldsymbol{h}^{i-1}\right)$中的每个元素就会很小，累乘会使最终结果很小，即梯度消失。

梯度消失带来的问题

• 梯度值变成0
  • 对16位浮点数尤为严重
• 训练没有进展
  • 不论学习率大小
• 对于底层部尤为严重
  • 仅仅顶层部（靠近输出的层）训练的较好
  • 神经网络无法加深

模型初始化和激活函数

如何让训练更加稳定，增加数值稳定性呢？

目标：让梯度值在合理的范围内，如[1e-6, 1e3]

方法：

• 将乘法变为加法。如：ResNet, LSTM
• 归一化。如：权重归一化、梯度裁剪（clipping）
• 合理的权重初始化和激活函数。

这里讲解“合理的权重初始化和激活函数”

motivation：让层间的方差为同一个常数

将每层的输出和梯度看作随机变量，让所有层间的均值和方差都保持一致。

即设计神经网络，使其对$\forall i, t$，有

正向传播时

$$\begin{aligned} \mathbb{E}\left[h_i^t\right] & =0 \\ \operatorname{Var}\left[h_i^t\right] & =a \end{aligned}$$

反向传播时

$$\begin{aligned} \mathbb{E}\left[\frac{\partial \ell}{\partial h_i^t}\right] &= 0 \quad \\ \operatorname{Var}\left[\frac{\partial \ell}{\partial h_i^t}\right] &= b \end{aligned}$$

其中，$a, b$为常数。

怎么达到这个要求呢？

权重初始化

对$h^t$层，

假设其权重$w_{ij}^t$都是从同一分布中独立抽取的。设该分布的均值和方差为$\mu=0, \sigma_t^2$（不一定是高斯/正态分布）。

假设其输入$h_i^{t-1}$也服从一个分布，设该分布的均值和方差为$\mu=0, \operatorname{Var}[h_i^{t-1}]$，且独立于$w_{ij}^t$。

假设没有激活函数，即$\boldsymbol{h}^t = \boldsymbol{W}^t\boldsymbol{h}^{t-1}, \boldsymbol{W}^t\in\mathbb{R}^{n_t \times n_{t-1}}$

正向传播时，经推导，有

$$\begin{aligned} \mathbb{E}[h_i^t] &= 0 \\ \operatorname{Var}[h_i^t] &= n_{t-1} \sigma_t^2 \operatorname{Var}[h_i^{t-1}] \end{aligned}$$

反向传播时，经推导，有

$$\begin{aligned} \mathbb{E}\left[\frac{\partial \ell}{\partial h_i^{t-1}}\right] &= 0 \\ \operatorname{Var}\left[\frac{\partial \ell}{\partial h_i^{t-1}}\right] &= n_t \sigma_t^2 \operatorname{Var}\left[\frac{\partial \ell}{\partial h_j^t}\right] \end{aligned}$$

为了使得层间的方差保持一致，那么必须有

$$\begin{aligned} n_{t-1} \sigma_t^2 &= 1 \\ n_t \sigma_t^2 &= 1 \end{aligned}$$

但这个条件难以满足，但我们可以满足两式平均得到的条件

$$\frac{n_{t-1} + n_t}{2} \sigma_t^2 = 1$$

即

$$\sigma_t^2 = \frac{2}{n_{t-1} + n_t}$$

这就是Xavier初始化的基础：通过该层的输入数量和输出数量确定权重分布的方差。

若采用正态分布，有

$$N(0, \frac{2}{n_\text{in} + n_\text{out}})$$

若采用均匀分布，有

$$U(-\sqrt{\frac{6}{n_\text{in} + n_\text{out}}}, \sqrt{\frac{6}{n_\text{in} + n_\text{out}}})$$

Note. 为保持均值为0，$U(a, b)$中$a=b$；为保证方差为$\frac{2}{n_\text{in} + n_\text{out}}$，$U(a, a)$的方差$\frac{a^2}{3} = \frac{2}{n_\text{in} + n_\text{out}}$。

Xavier初始化是很常用的一种初始化方法。

合适的激活函数

假设激活函数是线性的（事实上不使用，网络不会产生非线性、万有逼近能力），即$\sigma(x) = \alpha x + \beta$

设

$$\boldsymbol{h}^t = \sigma(\boldsymbol{h}^\text{temp}), \boldsymbol{h}^\text{temp} = \boldsymbol{W}^t\boldsymbol{h}^{t-1}$$

同时，有

$$\frac{\partial{\ell}}{\partial{\boldsymbol{h}^{t-1}}} = \alpha \frac{\partial{\ell}}{\partial{\boldsymbol{h}^\text{temp}}}\frac{\partial\boldsymbol{h}^\text{temp}}{\partial\boldsymbol{h}^{t-1}}, \frac{\partial\boldsymbol{h}^\text{temp}}{\partial\boldsymbol{h}^{t-1}} = \boldsymbol{W}^t$$

正向传播时，经推导，有

$$\begin{aligned} \mathbb{E}[h_i^t] &= \beta \\ \operatorname{Var}[h_i^t] &= \alpha^2 \operatorname{Var}[h_i^\text{temp}] \end{aligned}$$

为满足motivation，需要

$$\begin{aligned} \beta &= 0 \\ \alpha &= 1 \end{aligned}$$

反向传播时，经推导，有

$$\begin{aligned} \mathbb{E}\left[\frac{\partial \ell}{\partial h_i^{t-1}}\right] & =0 \\ \operatorname{Var}\left[\frac{\partial \ell}{\partial h_i^{t-1}}\right] & =\alpha^2 \operatorname{Var}\left[\frac{\partial \ell}{\partial h_i^\text{temp}}\right] \end{aligned}$$

为满足motivation，需要

$$\alpha = 1$$

即$\sigma(x) = x$时，满足motivation，训练更稳定。

为此，我们使用泰勒展开检查常用激活函数

$$\begin{aligned} \operatorname{logistic}(x) & =\frac{1}{2}+\frac{x}{4}-\frac{x^3}{48}+O\left(x^5\right) \\ \tanh (x) & =0+x-\frac{x^3}{3}+O\left(x^5\right) \\ \operatorname{ReLU}(x) & =0+x \quad \text { for } x \geq 0 \end{aligned}$$

其中，$\tanh(x), \operatorname{ReLU}(x)$在零点附近近似$f(x) = x$，这也从数值稳定性角度解释了这二者为何效果比较好。

为使得logistic函数在零点附近也近似$f(x) = x$，我们对其进行调整，即

$$\operatorname{scaled logistic}(x) = 4 \times \operatorname{logistic}(x) - 2$$

这样得到的scaled logistic函数，在零点附近时即为identity function / $f(x) = x$，可以解决掉logistic函数存在的问题。

QA

Q：nan, inf产生的原因？解决方法？

A：inf就是今天讲到的原因（lr太大，权重初始值太大），nan（Not A Number）一般是因为除零，如梯度值较小时将其除零；调小学习率，调小方差，直到正确计算出值，然后再调大使得训练有进展。

---