竞赛习惯
若精度要求为小数点后x位,则
esp = 1e-(x + 2),eg. 精度为小数点后6位,esp = 1e-8规模:$10^9$——大,$10^5$——小
没给范围默认为$10^6$
范围为$10^6$时优先考虑$O(nlogn)$、$O(n)$做法
$m\approx n$:稀疏图,$m\approx n^2$ :稠密图
评测机每秒可以计算$10^8$个数据,可以先根据欲使用算法的时间复杂度算一下数据量(详见AcWing 1624 我的题解)
常用简写:
i != 0:i,判断非0i != -1:~i,判断链表尾(NULL)u / 2:u << 1,完全二叉树中的左子结点u / 2 + 1:u << 1 | 1,完全二叉树中的右子结点(左移后最后1位一定是0,在这时0 | 1 = 1等价于0 + 1 = 1)i % 2 == 1:i & 1,判断奇数
关于7
1 |
|
1 | 0 |
所以当~i作为for循环终止条件时会在i为$-1$时退出循环。
调试技巧
- cout大法:输出中间变量
- 删:删掉可能ERROR的代码
- exit(0):相当于把
exit(0)后面的都删掉,eg. 可放在建图代码后用于判断是否为建图问题 - iii大法:用于查看算法在某段的输出,eg. 查看前十次输出
int iii = 0,cout << ver << endl; if ( ++ iii > 10) exit(0);,详见AcWing 1624。 - !、!!、!!!:在关键语句后添加
, puts("!")以查看其是否执行,详见Acwing1628 - out():二维矩阵可以写个out函数查看
树
给定任意两种遍历序列都可以确定二叉树,但只根据前序遍历和后序遍历无法确定唯一二叉树。eg. AcWing 1497. 树的遍历 AcWing 1609. 前序和后序遍历
二叉搜索树(BST):它的前序遍历为升序排序, 它的镜像的前序遍历记为降序排序。eg. AcWing 1527. 判断二叉搜索树
通过insert建树 eg. AcWing 1605. 二叉搜索树最后两层结点数量
1
2
3
4
5
6
7
8
9
10
11
12
13void insert(int &u, int w)
{
if (!u) // u == 0:没有结点,为其分配索引并赋值
{
u = ++ idx;
v[u] = w;
}
else
{
if (w <= v[u]) insert(l[u], w);
else insert(r[u], w);
}
}完全二叉树(CST):可以使用一个下标自1起的数组作为其结构,左子结点
2 * u,右子结点2 * u + 1。其判断方法:判断最大索引和结点个数的大小关系。eg. AcWing 1550. 完全二叉搜索树1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21void dfs(int u, int k)
{
if (u == -1) return ;
if (k > maxk)
{
maxk = k;
maxid = u;
}
dfs(l[u], 2 * k);
// tr[k] = u;
dfs(r[u], 2 * k + 1);
}
...
if (maxk == n) printf("YES %d\n", maxid);
else if (maxk > n)printf("NO %d\n", root); // 最大索引超过结点个数,说明层序遍历不连续,有空缺结点
...使用树的非递归遍历形式还原树需要记录上一次操作 eg. AcWing 1576. 再次树遍历
找根:eg. AcWing 1589. 构建二叉搜索树
1
2
3
4
5
6
7
8
9
10
11
12
13
14...
cin >> n;
for (int i = 0; i < n; i ++ )
{
int x, y;
cin >> x >> y;
l[i] = x, r[i] = y;
has_parent[x] = has_parent[y] = true;
}
int root;
while (has_parent[root]) root ++ ;
...反转二叉树 eg. AcWing 1592. 反转二叉树
1
2
3
4
5
6
7
8void tree_reverse(int u)
{
if (u == -1) return ;
tree_reverse(l[u]);
tree_reverse(r[u]);
swap(l[u], r[u]);
}PAT评测环境下:
树遍历可以传入已打印数量k的引用以控制最后一个空格1
2
3
4
5
6
7
8
9void dfs(int u, int &k)
{
if (u == -1) return ;
dfs(l[u], k);
cout << u;
if ( ++ k != n) cout << ' ';
dfs(r[u], k);
}特殊地,前序遍历可以传入两个root以控制第一个空格
AVL树:一种自平衡二叉搜索树,其左旋、右旋:就是将不平衡的结点“松弛”,也就是说没有向上的力拽着它,然后固定它的子树,那么问题结点就会自然往下掉,如果问题结点下落的一侧有结点,那么将其及其子树滑落到下落结点的另一侧。每次插入完成后共有四种不平衡情况 eg. AcWing 1552. AVL树的根
- ‘/‘型:不平衡结点为88,断开70——80,让88自然落下
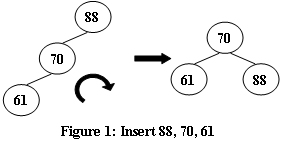
- ‘\\‘型:不平衡结点为88,断开70——88,让88自然落下
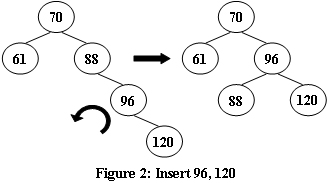
- ‘>‘型(70——96——88):断开70——96,96滑落至88右侧,88右侧原来的90滑落到96左侧,形成’\\’型(70——88——96),取消70的“顶点拉力”,让70自然落下
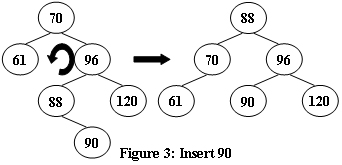
- ‘<‘型(70——61——65):不平衡结点为70,断开70——61,让61自然下落,形成’/‘型(70——65——61),断开70——65,让70自然落下
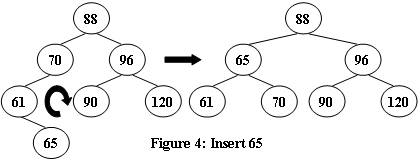
注:自然落下后裸露出的顶点接回此前上方断开的结点,另外yxc老师是按照这里的1、2、4、3讲的。另外,虽然流程上是先下落(旋转)后让冲突侧子树下滑,但是代码更新时要先让冲突侧子树下滑
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53void update(int u)
{
h[u] = 1 + max(h[l[u]], h[r[u]]);
}
int get_balance(int u)
{
return h[l[u]] - h[r[u]];
}
void L(int &u)
{
int p = r[u]; // 固定右子树
r[u] = l[p], l[p] = u; // 这里要先操作多余的结点,不是按思维顺序的,可以先理清关系再写
update(u), update(p);
u = p; // 更新根的索引
}
void R(int &u)
{
int p = l[u];
l[u] = r[p], r[p] = u;
update(u), update(p);
u = p;
}
void insert(int &u, int w)
{
if (!u) u = ++ idx, v[u] = w;
else
{
if (w < v[u])
{
insert(l[u], w);
if (get_balance(u) == 2)
{
if (get_balance(l[u]) == 1) R(u); // 情况1:'/'
else if (get_balance(l[u]) == -1) L(l[u]), R(u); // 情况3:'<'
}
}
else
{
insert(r[u], w);
if (get_balance(u) == -2)
{
if (get_balance(r[u]) == -1) L(u); // 情况2:'\'
else if (get_balance(r[u]) == 1) R(r[u]), L(u); // 情况4:'>'
}
}
}
update(u);
}红黑树(RBT):是一种平衡二叉搜索树,具有以下五个属性。eg. AcWing 1628. 判断红黑树
节点是红色或黑色。
根节点是黑色。
所有叶子都是黑色。(叶子是 NULL节点)
每个红色节点的两个子节点都是黑色。
从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。(可以递归判断:对每一个结点判断其左子树和右子树的黑色结点数目,自身使用引用传递自身树黑色结点数目(返回值用来传递根的权值了))
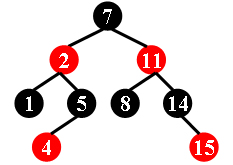
其中加粗的部分是RBT的充分条件,判断RBT时只需判断他们是否成立即可。
将无向图视作树遍历以求最深根结点的时候记得在dfs里加
if (j == father) continue防止走回头路。 eg. AcWing 1498. PAT 1021. 最深的根如果要求从根节点遍历到指定叶节点的深度,可以使用反向dfs + 记忆化搜索 eg. AcWing 1565. 供应链总销售额
将堆视作树遍历以判断其是大根堆还是小根堆时,建立;两个特征
bool gt, lt;gt: is_greater,大根堆特征(路径前一点权值大于后一点权值), lt: is_less,小根堆特征(路径前一点权值小于后一点权值)。如果兼具两个特征说明不是堆另外,堆是一种完全二叉树。
trick:
输出二叉树的后序遍历的第一个数字。只需要在左右遍历后加入
if (!post_first) post_first = root;只有第一个没有左右儿子的点才会到达并执行这行 eg. AcWing 1631. 后序遍历Z 字形遍历 eg. AcWing 1620. Z 字形遍历二叉树
注意reverse范围[first, last)
牢记中序遍历:root左侧是左子树,右侧是右子树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18void bfs(int root)
{
q[ ++ tt] = root;
int depth = 0;
while (hh <= tt)
{
int start = hh, end = tt;
while (hh <= end)
{
int t = q[hh ++ ];
if (l.count(t)) q[ ++ tt] = l[t];
if (r.count(t)) q[ ++ tt] = r[t];
}
if ( ++ depth % 2) reverse(q + start, q + end + 1);
}
}由任意两序还原二叉树,构建子树时的build(…)代码长度一样
1
2if (il < k) lchild = build(il, k - 1, pl + 1, pl + 1 + k - 1 - il, lsum);
if (ir > k) rchild = build(k + 1, ir, pl + 1 + k - 1 - il + 1, pr, rsum);
数论
欧拉筛法
刻进DNA!!数论题必考它!!!
因能在线性时间 $O(n)$ 内筛选出素数集合,故又称线性筛法。
先给出代码,之后给出正确性证明
1 |
|
欧拉筛法的时间复杂度优于埃氏筛法的原因就在于:
- 埃氏筛法的一个合数可能被它的多个质因数重复筛去
- 欧拉筛法的一个合数只会被它的最小质因数筛去
那么其正确性需要证明两点:
所有合数都会被筛去
$proof:$
假设任意合数 $ x = p * x_0$ ,其中 $ p $ 是 $ x $ 的最小质因子,那么 $ x_0 $ 即为 $ x $ 的最大因子。显然地,有 $ p \leq x_0 < x$ 。
当筛法遍历至 $ p $ 时,因 $ p $ 为素数,故有 $ p \in primes $ 。
当筛法遍历至 $ x_0 $ 时,必会执行
st[primes[j] * i] = true;( $ i = x_0, prime[j] = p$)将 $ x $ 筛掉。即任意合数 $ x $ 必会在算法遍历至 $ x_0 $ 时被筛掉
$ Q.E.D$
每个合数只会被其最小质因数筛去(没有重复筛去)
$ proof: $
因
if (i % primes[j] == 0) break;及$primes[j]$递增,所以筛法中的$primes[j]$必小于等于 $i$ 的最小质因数 $p$ 。当筛法执行时
若
i % primes[j] != 0,则$primes[j] < p$,$primes[j]$ 是合数 $primes[j] * i$ 的最小质因数若
i % primes[j] == 0,则$primes[j] = p$,$primes[j]$ 仍是合数 $primes[j] * i$ 的最小质因数即每个合数只会被其最小质因数筛去。
$ Q.E.D$
内层循环枚举质数的条件为primes[j] <= n / i是因为其等价于 $ primes[j] * i \leq n$,即被筛合数应小于指定范围 $ n $。
也不需要加 j < cnt防止越界,因为:
当 $i $ 为合数时, $primes[j]$ 枚举至 $i$ 的最小质因子 $ p $ 时一定会break;,此时必有$ p = primes[j] \in primes $ 。
当 $i $ 为质数时,$primes[j]$ 枚举至 $i$ 时一定会break;而 $i = primes[j]$刚刚在上一行被加入 $primes$ ,故仍必有$ primes[j] \in primes $ 。
另外,一个显然的事情,st[primes[j] * i] = true;筛去的是一个乘积,它必是一个合数。
欧拉函数$ {\varphi (n)} $
若
则
其值为 小于等于n的正整数中与n互质的数的数目。
时间复杂度:$O(\sqrt n)$
由来:容斥原理
……..
if (i % primes[j] == 0)
此时 $primes[j]$ 等于 $i$ 的最小质因数 $ p_1 $ ,故 和 的质因数完全相同,只需更换第一项为 。
if (i % primes[j] != 0)
此时 $primes[j]$ 小于 $i$ 的最小质因数 $ p_1 $,又因其是质数,故 比 多出一个质因数 ,因此需要更换第一个因数为 并增加一项 。
求逆元
由费马小定理($Fermat’s\ little\ theorem$)求逆元
假如 ${a}$ 是一个整数, ${p}$ 是一个质数,如果 $ a$ 不是 $p$ 的倍数,那么
其等价于
那么 $a^{p-2}$ 即为 $a$ 的逆元。
使用扩展欧几里得算法求逆元
扩展欧几里得算法不要求模数为质数,但要求$x$ 、$m$ 互质。
同余方程
其等价一般方程:
令 $y = -y$ ,有裴蜀等式:
由裴蜀定理,当且仅当
时,裴蜀等式有解。
即 $d = 1$ ,$x$ 、$m$ 互质时,$a$ 有逆元。
一次同余方程组
一次同余方程组有两种形式:
- 模数 $m_1, m_2, \dots, m_n$两两互质
- 模数 $m_1, m_2, \dots, m_n$不两两互质
对于情况1,可使用中国剩余定理或一般解法;
对于情况2,则只能使用一般解法。
一般解法:
两个同余方程时:
其等价的一般方程形式:
联立,有裴蜀等式(右侧的等式):
令 $k_2 = -k_2$,移项,有:
由裴蜀定理,当且仅当时,裴蜀等式有整数解。
有解时,使用扩展欧几里得算法,可求得方程
的一组可行解
两侧同乘,可得原方程的一组可行解
又由裴蜀定理,可得原方程的通解
又
所以要求最小非负整数 $x$ ,就要求最小非负整数 $k_1$ ,只需
此时即可得方程组的最小非负解
最后,使用原方程组通解 进行推导得到通解的同余形式以进行多个同余方程时的运算
即:
与原式同构,可得更新方程:
组合数学
根据数据量的不同,可以使用不同复杂度的方法解题。
预处理结果
由组合数递推公式预处理结果,时间复杂度$O(n^2)$ $eg. 1\leq b\leq a\leq 2000$
从 $a$ 个元素中选取 $b$ 个元素,等价于:对于某个元素,
若选取它,则还需从剩余 $a - 1$ 个元素中选取 $b - 1$ 个元素;
若不选取它,则还需从剩余 $a - 1$ 个元素中选取 $b$ 个元素。
预处理阶乘及其逆元
预处理阶乘及其逆元,时间复杂度$O(nlogn)$ $eg. 1\leq b\leq a\leq 10^5$
在同余式中可以将除数视作逆元,如下
两个 $ 10^9 $相乘不会在 $ long\ long $ 范围内溢出 ,三个会。
mod = 1e9 + 7是比1e9大的第一个质数
阶乘递推公式(定义)
对等式取逆得阶乘逆元递推公式
卢卡斯定理
卢卡斯定理($Lucas’s\ theorem$)时间复杂度 $eg. 1\leq b\leq a\leq 10^{18},1 \leq p \leq 10^5$
一次递归:
最终把a, b变成p进制
分解质因数
分解质因数,将阶乘转换为乘法,这样也可以进行高精度运算。
即
我们可以通过枚举所有素数 ,计算所有 ,就是先计算 中 的个数,然后再减去 和 中 的个数即可。
卡特兰数
卡特兰数()
卡特兰数有多种常见公式。
卡特兰数列往往包含很多问题的解,所以重要的是分析出问题的规律以应用卡特兰公式。
| $H_0$ | $H_1$ | $H_2$ | $H_3$ | $H_4$ | $H_5$ | $H_6$ | $\dots$ |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 5 | 14 | 42 | 132 | $\dots$ |
关于卡特兰数的更多知识包含在这里:OEIS A000108
这里给出一种构造性证明方法:
$ proof: $
考虑含 $n$ 个 $+1$ 、$n$ 个 $-1$ 的所有序列,长度为 $2n$。
其中满足前缀和条件
的序列的数量即为卡特兰数 。
首先,含 $n$ 个 $+1$ 、$n$ 个 $-1$ 的所有序列,长度为 $2n$ 的序列数量共有 。
考虑由 个 和 个 组成的序列 ,可知,其数量为 。
其必存在 使得 且 的数量比 的数量多 $1$ 。
令
则
且含 $n$ 个 $+1$ 、$n$ 个 $-1$ (对前 $m$ 个数取相反数后, 的数量比 的数量少 $1$ )。
那么序列 即为不满足前缀和条件的序列,其数量为 或 。
即可得满足前缀和条件的序列的数量为 。
$Q.E.D$
组合恒等式
等式两侧的意义均为从n个数中选出任意个数的方案数量。
$proof:$
由二项式定理得:
$Q.E.D$
博弈论
有向图游戏
有向图游戏是一个经典的博弈游戏——实际上,大部分的公平组合游戏(Impartial Combinatorial Games,ICG)都可以转换为有向图游戏。
在一个有向无环图(DAG)中,只有一个起点,上面有一个棋子,两个玩家轮流沿着有向边推动棋子,不能走的玩家判负。
Nim游戏
$n$ 堆物品,每堆有 $a_i$ 个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。
取走最后一个物品的人获胜。
首先我们知道:
败态:
接着,我们可以按异或和是否为0将所有状态分为两类:状态1和状态2
状态1:
状态2:
再然后,若操作者足够聪明,我们可以发现两件事情:
- 对状态1操作后一定会转移至状态2
- 对状态2操作后一定会转移至状态1
先证明1:
$proof:$
设 $x$ 中二进制最高位 $1$ 在第 $k$ 位
则必存在 $a_i$ 的第 $k$ 位为 $1$,即
(因为操作者足够聪明,他知道若想将此状态转移至状态2只需在两侧同时异或 $x$ ,也就是将 $a_i$ 变为 $a_i \oplus x$,所以他做了如下操作)
从$a_i$堆中拿走 $a_i-a_i \oplus x$ 个石子,因为 $a_i$ 和 $ a_i \oplus x $ 位数相同,且 $ a_i \oplus x $ 在第 $k$ 位上为 $0$,$ a_i $ 在第 $k$ 位上为 $1$ ,所以 $a_i-a_i \oplus x > 0$ ,操作合法。
那么操作后 $a_i$ 堆剩余 $ a_i - (a_i-a_i \oplus x) = a_i \oplus x$ 个石子,新状态为:
即状态2
$Q.E.D$
再证明2:
$proof:$
假设对状态2操作后仍在状态2。
若拿取第 $a_i$ 堆,拿取后变为 $a_i^{\prime}$,$ a_i^{\prime} < a_i $
拿取前:
由假设,拿取后:
对两式进行异或,有:
与 $ a_i^{\prime} < a_i $ 矛盾,故假设不成立,原命题成立。
$Q.E.D$
从这两件事情我们可以发现,拿到状态2的人永远只会在状态2
又因为每人每次拿走石子的数量 $\geq$ 1,
所以在状态2的人,他的石子数量一定会单调递减,最后转移至败态。
所以我们称状态1为必胜态,状态2为必败态。
因此我们可以通过判断初态的异或和为 $0$ 与否,去判断先手方是否必胜,也就是:
初态异或和不为0时,先手方必胜。
初态异或和为0时,先手方必败。
斯普莱格–格隆第定理(S-G定理)
斯普莱格–格隆第定理($Sprague–Grundy\ theorem$)
该定理指出,所有的一般胜利条件下的无偏博弈都能转换成单堆Nim游戏或其无限泛化。
定理做如下定义:
$mex$ (minimum exclusion):译作“最小排除”,意为良序集合的补集的最小值。
即:
对于状态 $x$ 和它的所有 $k$ 个后继状态 $y_1, y_2, \dots, y_k$ ,定义 $SG$ 函数:
注:${\operatorname {mex} (\emptyset )=0}$,即终点状态的 $SG$ 值为 $0$ 。
那么,
对于由 $n$ 个有向图游戏组成的组合游戏,设它们的起点分别为 $s_1, s_2, \dots, s_n $,当且仅当
时,先手方必胜。即:
初态sg异或和不为0时,先手方必胜。
初态sg异或和为0时,先手方必败。
证明方法类似Nim游戏。
同时,还是该组合游戏的 $SG$ 值。(可以用在新状态有多个子状态时计算新状态的SG值,eg. AcWing 894. 拆分-Nim游戏)
eg. AcWing 893. 集合-Nim游戏(每堆石子对应一个DAG)
动态规划
背包DP
闫学灿热狗模型
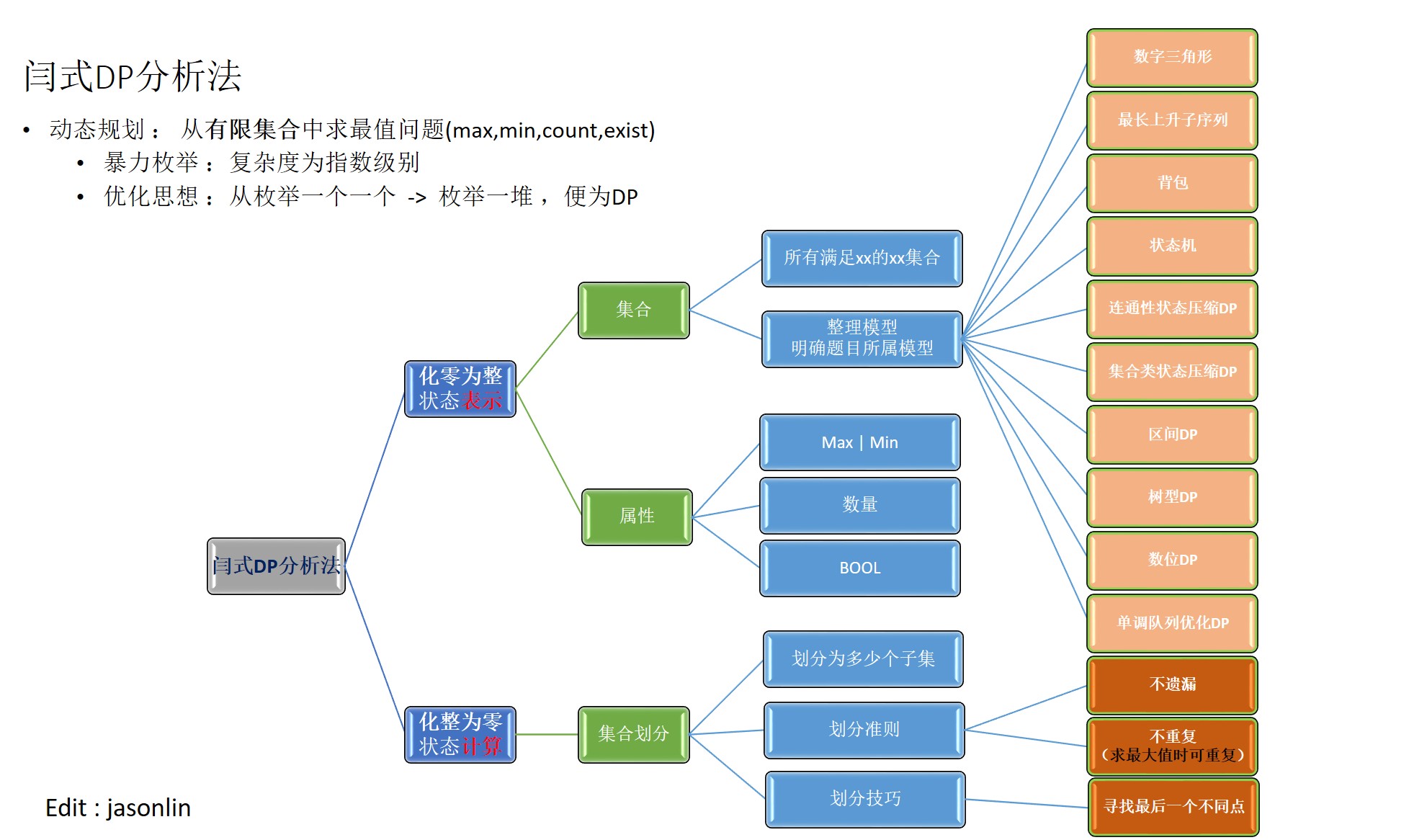
0-1背包
有 $N$ 件物品和一个容量是 $V$ 的背包。每件物品只能使用一次。
第 $i$ 件物品的体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
在这种问题中,每件物品的数量的取值域为 $\{0, 1\}$,故称0-1背包问题。
写作最优化形式,即为:
完全背包
有 $N$ 件物品和一个容量是 $V$ 的背包。每种物品都有无限件可用。
第 $i$ 件物品的体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
输出最大价值。
在这种问题中,每件物品的数量的取值域为 ${\mathbb {N} _{0}=\mathbb {N} ^{0}=\{0,1,2,\dots \}}$,故称完全背包问题,国际上称无界背包问题(unbounded knapsack problem, UKP)。
最优化形式:
多重背包
有 $N$ 种物品和一个容量是 $V$ 的背包。
第 $i$ 种物品最多有 $s_i$ 件,每件体积是 $v_i$,价值是 $w_i$。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
输出最大价值。
在这种问题中,每件物品的数量的取值域为 $ \{0,1,2,\dots , s_i \} $,故称多重背包问题,国际上称有界背包问题(bounded knapsack problem , BKP)
最优化形式:
分组背包
有 $N$ 组物品和一个容量是 $V$ 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 $v_{ij}$,价值是 $w_{ij}$,其中 $i$ 是组号,$j$ 是组内编号。求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
输出最大价值。
线性DP
特征:状态的推导是按照问题规模 i 从小到大依次推过去的,较大规模的问题的解依赖较小规模的问题的解。
区间DP
特征:求一个区间的最优值,一个区间的最优值由两个或多个小区间合并而来。
DP问题的起始下标选择:若状态转移方程中含有f[i - 1],那么令i的起始下标为1;若不含,则可为0。
$状态转移方程的时间复杂度 = 状态数量(方程左边) \times 转移数量(方程右边)$
经验积累
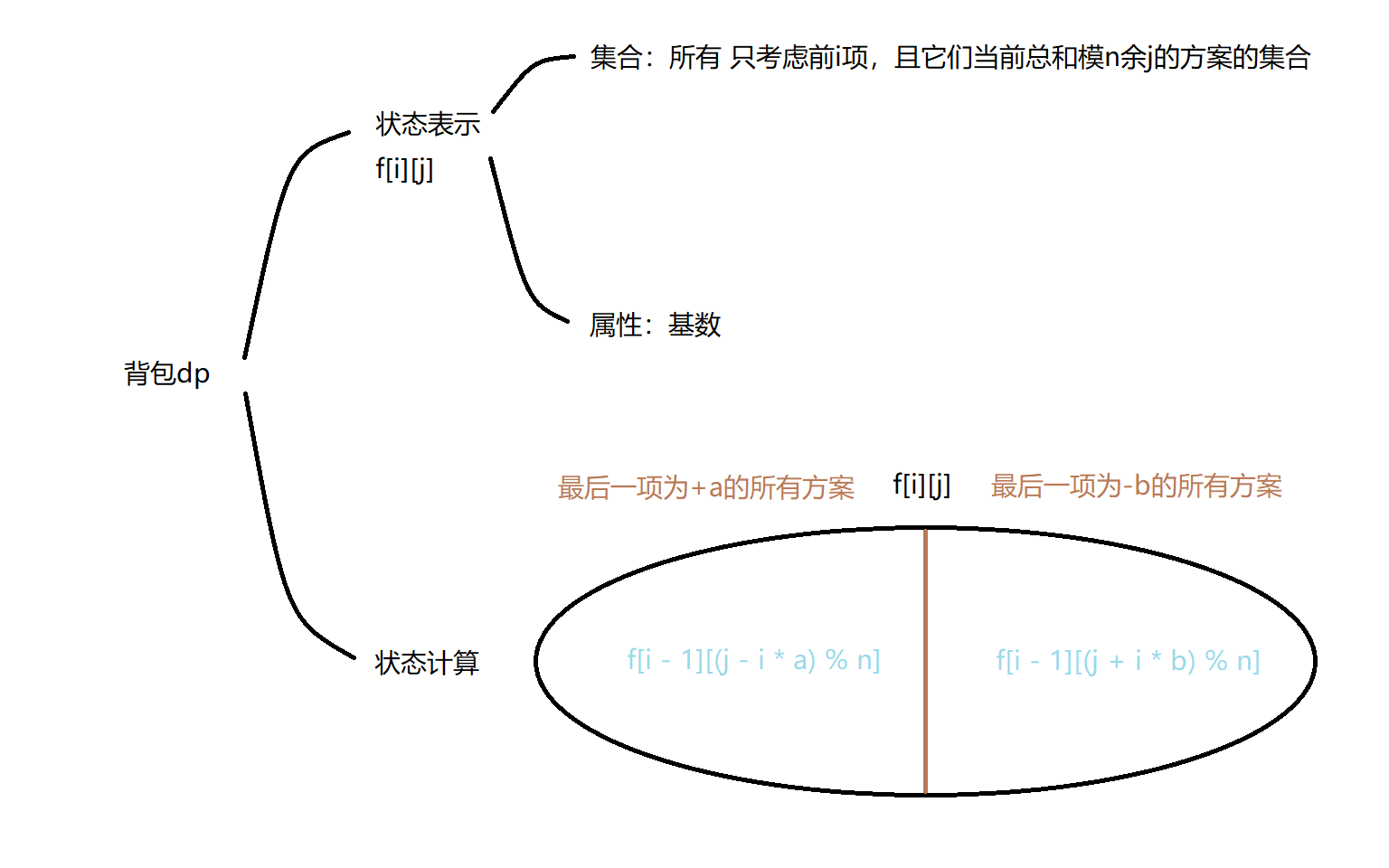
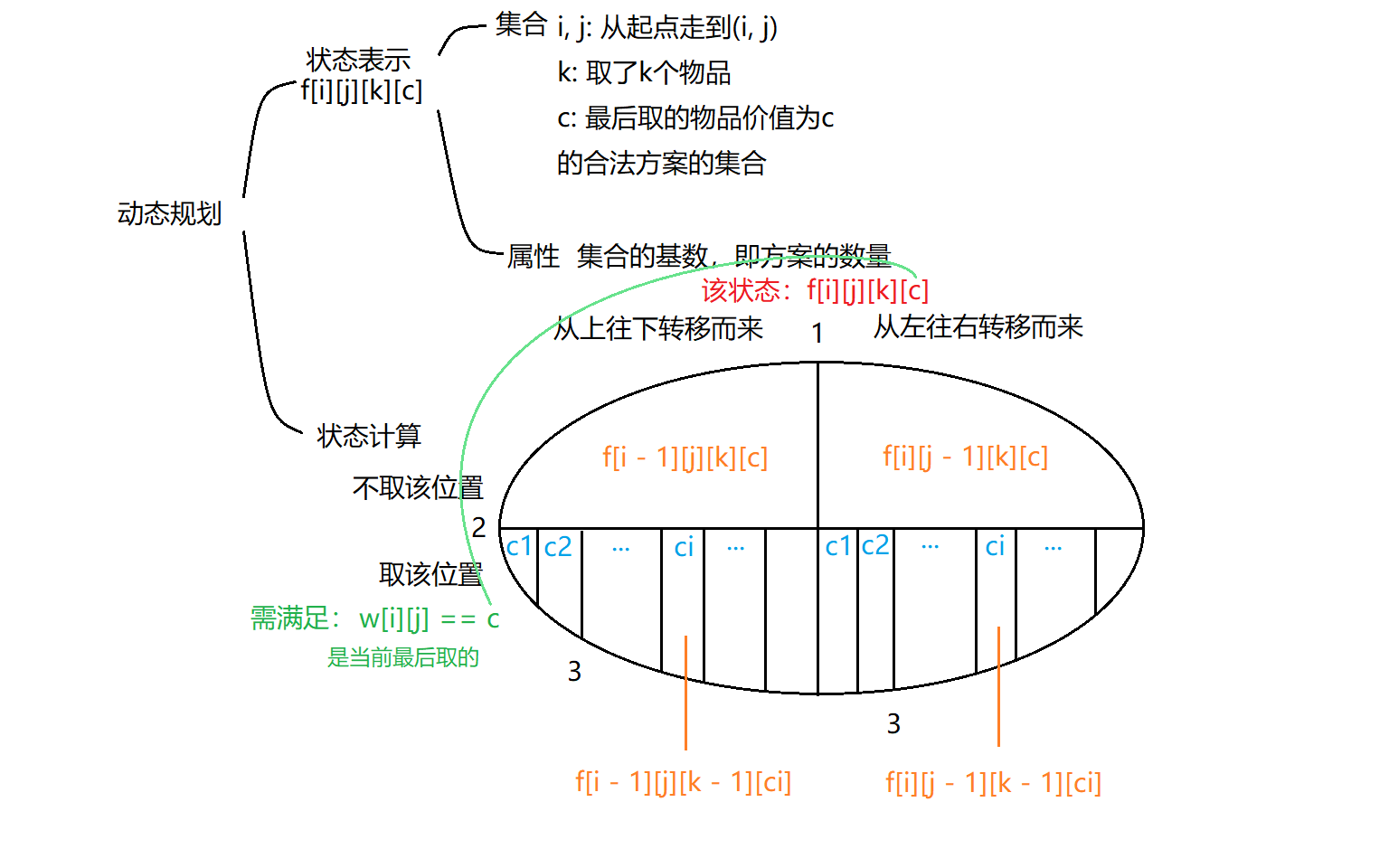
时空复杂度分析
看起来,我们已经学完了大部分内容!
但是,怎么根据题目、范围来选定算法呢?没有这第0步,我们后面的步就容易白给。
由数据范围反推算法复杂度以及算法内容
这部分转自闫学灿老师。
一般ACM或者笔试题的时间限制是1秒或2秒。
在这种情况下,C++代码中的操作次数控制在 $10^7∼10^8$ 为最佳。
下面给出在不同数据范围下,代码的时间复杂度和算法该如何选择:
$n \leq 30 \Rightarrow$ 指数级别 :dfs+剪枝,状态压缩dp
$n≤100 \Rightarrow O(n^3)$ :floyd,dp,高斯消元
$n≤1000 \Rightarrow O(n^2), O(n^2logn)$ :dp,二分,朴素版Dijkstra、朴素版Prim、Bellman-Ford
$n≤10000 \Rightarrow O(n∗\sqrt{n})$ :块状链表、分块、莫队
$n≤100000 \Rightarrow O(nlogn)$ :各种sort,线段树、树状数组、set/map、heap、拓扑排序、dijkstra+heap、prim+heap、Kruskal、spfa、求凸包、求半平面交、二分、CDQ分治、整体二分、后缀数组、树链剖分、动态树
$n≤1000000 \Rightarrow O(n)$, 以及常数较小的 $O(nlogn)$ 算法 : 单调队列、 hash、双指针扫描、并查集,kmp、AC自动机,常数比较小的 $O(nlogn)$ 的做法 :sort、树状数组、heap、dijkstra、spfa
$n≤10000000 \Rightarrow O(n)$ :双指针扫描、kmp、AC自动机、线性筛素数
$n≤10^9 \Rightarrow O(\sqrt{n})$ :判断质数
$n≤10^{18} \Rightarrow O(logn)$ :最大公约数,快速幂,数位DP
$n≤10^{1000} \Rightarrow O((logn)^2)$ :高精度加减乘除
$n≤10^{100000} \Rightarrow O(logk×loglogk)$ :k表示位数,高精度加减、FFT/NTT
作者:yxc
链接:https://www.acwing.com/blog/content/32/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
时间复杂度
空间复杂度
静态分析方法
1 | 1 Byte = 8bit |
那么,$64MB$ 可使用$int$空间$ = \frac{64MB}{4Byte} = 16MB \approx 16\ 000\ 000 Byte$(可以开$16\ 000\ 000$个$int$)
动态分析方法
cout << (sizeof v + sizeof w + sizeof f) / 1024 / 1024 << "MB" << endl;
(sizeof返回size_t,单位为Byte)
注意:
因为操作系统使用虚拟内存技术,所以声明但未使用的空间不会被页面置换进内存,只有当被使用后才会占用内存。
$eg.$ Acwing 2. 01背包问题
1 |
|
memset代码段存在的话便会MLE,不存在的话即使其输出的$114MB > 64MB$也不会MLE。
递归算法
递归算法递归多少层(多深)压多少栈空间
$eg.$ AcWing 785. 快速排序
1 |
|
快速排序每层的时间复杂度为 $O(n)$,深度为 $log_2n$,故其时间复杂度为 $O(nlogn)$
Q:为什么只看深度不看递归的次数?
A:因为快速排序的递归树是一棵二叉树,快速排序过程类似于对其进行DFS,只有从根节点到当前遍历点那一条路径上的状态被压在栈空间中,离开当前状态后栈空间就被标记为回收了。
数学——推公式
这种题特征很明显,输入少、输出少、代码短(前提是知道公式解)
在没有题量基础时只能使用我为数不多的智商去推结论,然后一定把它要背下来
所以用例题讲一下怎么推公式,详见AcWing 1205. 买不到的数目、NOIP2017提高组. 小凯的疑惑
题意:
输入:两个数 $a$ , $b$
输出: $sa + tb$ 的最大不可凑数($s, t \in \mathbb{Z}^{+}$)
由裴蜀定理:
那么若 $a$ , $b$ 不互质,则必存在无穷多个不能被 $gcd(a, b)$ 整除的数
所以我们需要从互质的两数中找规律
若 $a$ , $b$ 互质且 $\in Z$ ,则有:
由裴蜀定理推论(和我记的推论形式不太一样,没细推,相信y总),有:
所以当m足够大时,一定能找到正整数解$(ma - b)\in Z^{+}$和$(mb + a)\in Z^{+}$
所以我们也只需考虑m较小时的情况,先写个暴力将其转换为找规律问题,m较小,取1000
暴力解(这个dfs也很灵活、不模板。。)
1 | import sys |
记录一些互质数的最大不可凑数1
2
3
4
5
6
7
8
9
10
11
12a b m
2 3 1
2 5 3
2 7 5
2 9 7
3 4 5
3 5 7
3 7 11
3 8 13
4 5 11
4 7 17
4 9 23
奥数规律题:两个变量时固定一个变量再找规律
$a = 2$时:
注意到 $b$ 每增加 $2$ ,$m$ 就增加 $2$ ,故$m \propto b$,$ m = b + x$,代入几组数据解得:
$a = 3$时:
注意到 $b$ 每增加 $1$ ,$m$ 就增加 $2$ ,故$m \propto 2b$,$ m = 2b + x$,代入几组数据解得:
$a = 4$时:
注意到 $b$ 每增加 $2$ ,$m$ 就增加 $6$ ,故$m \propto 3b$,$ m = 3b + x$,代入几组数据解得:
…
$a = a$时,归纳推理得:
事实上,归纳推理的结论是不准确的,但这个结论是对的,详见y总在NOIP《小凯的疑惑》处的证明
所以我们直接可以使用公式AC
公式解
1 | a, b = map(int, input().split()) |
python in ACM
记录与C++ in ACM/OI的诸多不同之处
定义
二维数组:[[0] * M for _ in range(N)](N行M列矩阵)
多维数组:用python原生数组创建多维数组,需要从高维度往低维度写,最高维度可以使用语法糖。
eg.
cpp
1 | int f[N][M][K]; |
python1
2
3
4
5
6f = [[[0] * K for _ in range(M)] for _ in range(N)]
# 我喜欢写成这样
f = [[ [0] * K \
for _ in range(M)] \
for _ in range(N)]
二者等价
输入输出
python以\n为分隔符,空行需要读入并扔掉!!(cpp以空白为分隔符)
将连续无分隔符的字符串str分解为字符可使用list(str),也可使用列表解析[i for i in str]
从(1, 1)输入的方式:先定义出0矩阵,然后对1 ~ n + 1行整体替换1 ~ m + 1列(对右下的大正方形按行输入)
eg.
cpp
1 | int w[N][M]; |
python
1 | w = [[0] * (m + 1) for _ in range(n + 1)] |
重定向方式:
1 | import sys |
注意:不能写from sys import stdin, stdout!!,python会把第3行的stdout当成文件变量!!!
循环
while(T -- )这种操作在没有海象运算符(while T := T - 1:)时最好使用for _ in range(T):或while T: T -= 1,循环变量可以帮助读入空行以判断EOF(if T: input())
python for循环侧重于for-each,range也只能对一元一次变量的范围做限制,如果想像cpp for那样使用复杂的进入表达式只能用while
cpp for:1
2
3
4for (init; condition; increment)
{
statement;
}
eg.1
2
3
4for (int i = 1; i * i <= n; i ++)
{
printf("%d\n", i);
}
python while:1
2
3
4init
while condition:
statement
increment
eg.1
2
3
4i = 0
while i * i <= n:
print(i)
i += 1
二者完全等价,不需要其他修改
python只能在自定义函数中返回,想在主函数中退出n层循环只能设置n - 1个标志变量flag/brk/rtn等
简写
可以使用连续判断语法糖
python也可以用逗号连接两句要执行的表达式
:语句块只有一行时也可以写在右侧
库
实现memcpy需要使用copy.deepcopy
python sort的对象中的元素若为列表,会将此列表作为联合主键排序(和cpp sort排PII类似,越靠前优先级越高)
运算规则
str和int不能异或
str不可更改,将其列表解析为列表
>>向下取整,eg. 125 >> 1 == 62
替代语法
引用:可以写个“手动引用”,修改前用新变量获取它的值,对新变量修改完成后再赋回去
eg.
1 | for i in range(1, n + 1): |
高级数据结构
树状数组
在 $O(logn)$ 的时间内
- 给某个位置上的数加上一个数(单点修改)
- 快速求前缀和(区间查询)
单点修改、区间查询是树状数组最常用的情况
树状数组与前缀和数组最大的区别在于其支持修改(在线算法)
树状数组的形态:
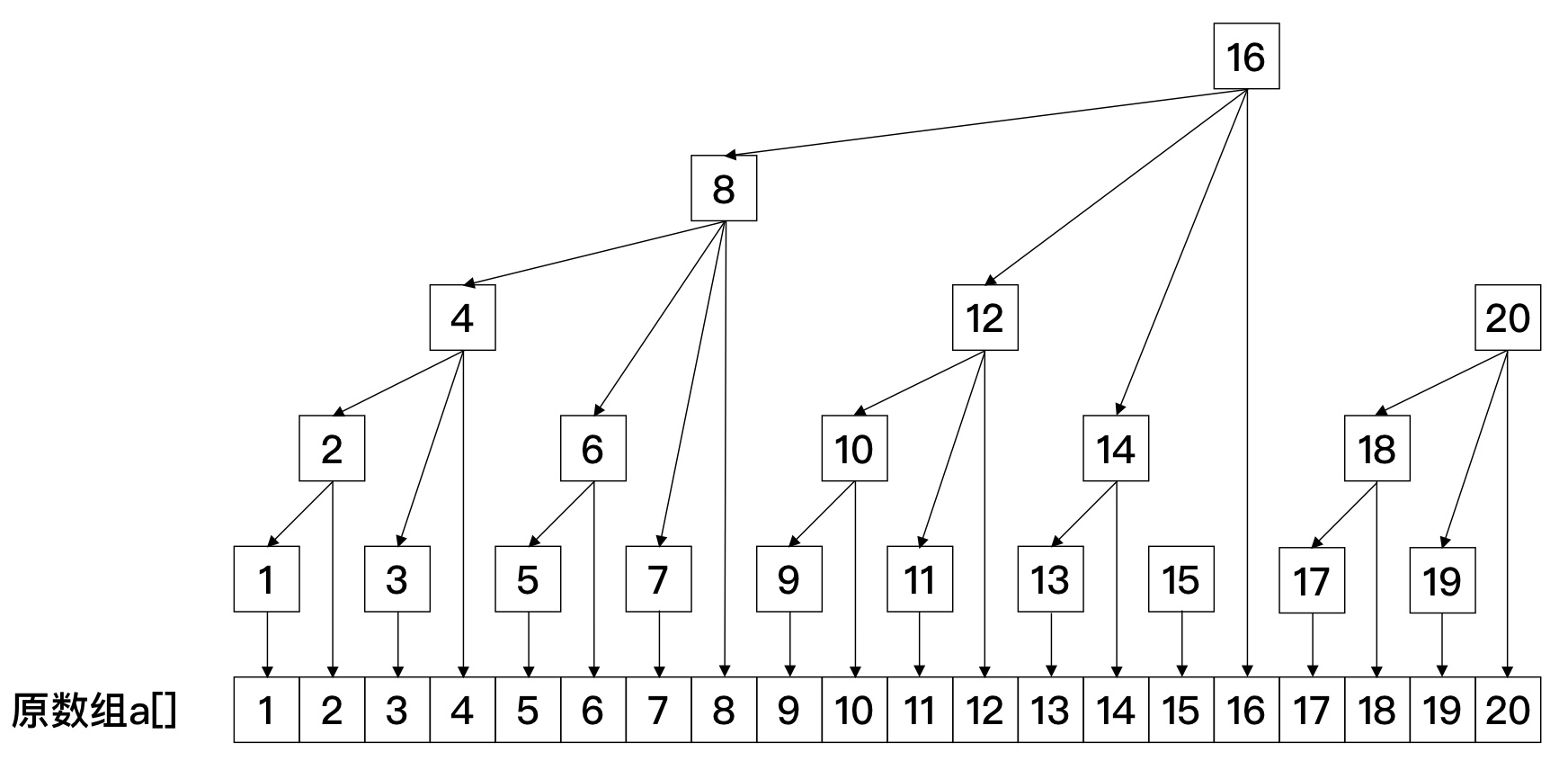
$c_x$ 在二进制表示下的后缀0段长度为k,则位于第k层。
每个 $c_x$ 存储原数组中 $(x - lowbit(x), x]$ 段的和。
三个基本操作:
lowbit(x):计算 $x$ 在二进制下末位1所代表的数值
1 | // cpp version |
1 | # python version |
add(x, v):欲单点修改原数组中的某一个数时,对树状数组的修改
1 | // cpp version1 |
1 | # python version1 |
query(x):查询 $(0, x]$ 段的和($x$ 前缀和)
1 | // cpp version1 |
1 | # python version1 |
线段树
线段树的形态:
常用情况:
- 单点修改、区间查询
- 区间修改、区间查询(lazy标记)
基本操作:
push_up:将信息向上传递
push_down:区间修改使用的操作,有时会被包含在其他操作中
build
modify
query
Q:为什么线段树需要开 $4 * N$ 个结点?
A:参考LeetCode 108. Convert Sorted Array to Binary Search Tree中证明的结论,可以得到线段树所有叶子节点必然在最下面的两层中。考虑倒数第二层的节点,其个数一定小于 $n$ ,那么从倒数第二层一直到根节点的节点数一定小于 $2n$ ,最后一层的节点数最多是是倒数第二层的两倍,那么也小于 $2n$ ,所以总共小于 $4n$ 。
用一段例题(AcWing 1264. 动态求连续区间和)的注释代码理解这些操作
1 | // cpp version |
1 | # python version |
第一讲 基础算法
快速排序
AcWing 785. 快速排序
1 |
|
AcWing 786. 第k个数
1 |
|
归并排序
AcWing 787. 归并排序
1 |
|
AcWing 788. 逆序对的数量
1 |
|
注意有一组数据的rst超过了int范围的上界,需要更大的空间。
二分
AcWing 789. 数的范围
1 |
|
二分形式上就是一个给定范围的while循环
AcWing 790. 数的三次方根
1 |
|
高精度
AcWing 791. 高精度加法
1 |
|
AcWing 792. 高精度减法
1 |
|
AcWing 793. 高精度乘法
1 |
|
AcWing 794. 高精度除法
1 |
|
前缀和与差分
AcWing 795. 前缀和
1 |
|
AcWing 796. 子矩阵的和
1 |
|
AcWing 797. 差分
1 |
|
二刷,发现这种与前缀和相逆的思路更好。
1 | N = 100010 |
AcWing 798. 差分矩阵
1 |
|
双指针算法
AcWing 799. 最长连续不重复子序列
1 |
|
AcWing 800. 数组元素的目标和
扔了拐棍还写得很顺,很开心
思路就是想办法构造出“单调”的情况,不然就变成暴力解O(n^2)了
最开始是想把两个指针放在一侧,但是可能会出现i前进,j后退也能满足解的情况,然后我就把其中一个指针放到了另一侧
以i右侧起,j左侧起为例,这样的话有三种情况:
- 若
a[i] + b[j] < x,因a有序,则a[i - 1] + b[j] < x必成立,这种情况只能让j + 1(向右),尝试从下侧接近x; - 若
a[i] + b[j] > x,因b有序,则a[i] + b[j + 1] > x必成立,这种情况只能让i - 1(向左),尝试从上侧接近x; - 若
a[i] + b[j + 1] == x,则找到结果。
因为双指针是for + while结构,那么取i为for中的循环变量,j为while中的循环变量即可。
用if捕获情况3,出现情况1时while对j进行右移,二者作用结束后剩下情况2,由for对i进行左移。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace std;
const int N = 100010;
int n, m, x;
int a[N], b[N];
int main(){
scanf("%d%d%d", &n, &m, &x);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
for (int i = 0; i < m; i ++ ) scanf("%d", &b[i]);
for (int i = n -1 , j = 0; i >= 0; i -- ){
while (a[i] + b[j] < x) j ++ ;
if (a[i] + b[j] == x){
printf("%d %d", i, j);
break;
}
}
return 0;
}
位运算
AcWing 801. 二进制中1的个数
1 |
|
AcWing 2816. 判断子序列
强套y总for + while板子写的,写完后发现while的j ++和外层for的j ++重复了,其实可以只用一个循环(y总wp)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using namespace std;
const int N = 100010;
int n, m;
int a[N], b[N];
int main(){
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
for (int j = 0; j < m; j ++ ) scanf("%d", &b[j]);
for (int i = 0, j = 0; i <= n; i ++ , j ++ ){ // 每次找到一对匹配的元素,然后再往后找
if (i == n){ // 遍历b前,若发现a遍历完了,则说明a是b的子序列
puts("Yes");
break;
}
while (j < m && a[i] != b[j]) j ++ ; // 单调遍历b中元素直到和a中某元素配对
if (j == m){ // 遍历b后,若发现b遍历完了,则说明a不是b的子序列
puts("No");
break;
}
}
return 0;
}
附y总代码,可见逻辑一样1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
using namespace std;
const int N = 100010;
int n, m;
int a[N], b[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
for (int i = 0; i < m; i ++ ) scanf("%d", &b[i]);
int i = 0, j = 0;
while (i < n && j < m)
{
if (a[i] == b[j]) i ++ ; // 找到一对匹配的元素,然后再往后找
j ++ ;
}
if (i == n) puts("Yes"); // 若发现a遍历完了,则说明a是b的子序列
else puts("No"); // 若发现b遍历完了,则说明a不是b的子序列
return 0;
}
离散化
AcWing 802. 区间和
CSP曾有一道稀疏向量的题。原理就是离散化。
直观上讲,就是将原数组进行“下标按序压缩”
为了防止压缩后的下标里没有查询的边界,把查询的边界也加进去。
1 |
|
区间合并
AcWing 803. 区间合并
1 |
|
第二讲 数据结构
单链表
AcWing 826. 单链表
显式head1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
using namespace std;
const int N = 100010;
int m;
int head, e[N], ne[N], idx; // head, elements, next elements, index
void init(){
head = -1;
idx = 0;
}
void add_to_head(int x){
e[idx] = x, ne[idx] = head, head = idx ++ ;
}
void add(int k, int x){
e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ; // 尾结点指向的-1始终存在,因为不论添加、删除,对后继节点都应理解为已有指针的移动(转动)
}
void remove(int k){
if (k == -1) head = ne[head]; // 这里k的-1代表头结点前面的head,ne[k]的-1才代表NULL
else ne[k] = ne[ne[k]];
}
int main(){
cin >> m;
init();
while (m -- ){
int k, x;
char op;
cin >> op;
switch(op){
case 'H':
cin >> x;
add_to_head(x);
break;
case 'D':
cin >> k;
remove(k - 1);
break;
case 'I':
cin >> k >> x;
add(k - 1, x);
break;
}
}
for (int i = head; i != -1; i = ne[i]) cout << e[i] << ' ';
return 0;
}
隐式head,跟这道题莫名契合1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
using namespace std;
const int N = 100010;
int m;
int e[N], ne[N], idx; //elements, next elements, index
void init(){
ne[0] = -1; // idx0作为head
idx = 1; // 第1个插入的元素位于下标1处
}
void insert(int k, int x){
e[idx] = x, ne[idx] = ne[k], ne[k] = idx ++ ; // 尾结点指向的-1始终存在,因为不论添加、删除,对后继节点都应理解为已有指针的移动(转动)
}
void remove(int k){
ne[k] = ne[ne[k]];
}
int main(){
cin >> m;
init();
while (m -- ){
int k, x;
char op;
cin >> op;
switch(op){
case 'H':
cin >> x;
insert(0, x);
break;
case 'D':
cin >> k;
remove(k);
break;
case 'I':
cin >> k >> x;
insert(k, x);
break;
}
}
for (int i = ne[0]; i != -1; i = ne[i]) cout << e[i] << ' ';
return 0;
}
双链表
AcWing 827. 双链表
1 |
|
栈
AcWing 828. 模拟栈
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
using namespace std;
const int N = 100010;
int m;
int stk[N], sp;
void push(int x){
stk[ ++ sp] = x; // stk[0]不存,用来判空
}
void pop(){
sp -- ;
}
void empty(){
puts(sp ? "NO" : "YES");
}
void top(){
cout << stk[sp] << endl;
}
int main(){
cin >> m;
while (m -- ){
string op;
cin >> op;
if (op == "push"){
int x;
cin >> x;
push(x);
}
else if (op == "pop") pop();
else if (op == "empty") empty();
else if (op == "query") top();
}
return 0;
}
STL1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
const int N = 100010;
int m;
stack<int> s;
int main(){
cin >> m;
while (m -- ){
string op;
cin >> op;
if (op == "push"){
int x;
cin >> x;
s.push(x);
}
else if (op == "pop") s.pop();
else if (op == "empty") puts(s.empty() ? "YES" : "NO");
else if (op == "query") cout << s.top() << endl;
}
return 0;
}
AcWing 3302. 表达式求值
1 |
|
队列
AcWing 829. 模拟队列
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
using namespace std;
const int N = 100010;
int m;
int q[N], hh, tt = -1;
void push(int x){
q[ ++ tt] = x;
}
void pop(){
hh ++ ;
}
void front(){
cout << q[hh] << endl;
}
void empty(){
puts( hh > tt ? "YES" :"NO");
}
int main(){
cin >> m;
while (m -- ){
string op;
cin >> op;
if (op == "push"){
int x;
cin >> x;
push(x);
}
else if(op == "pop") pop();
else if(op == "empty") empty();
else if(op == "query") front();
}
return 0;
}
STL1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
using namespace std;
const int N = 100010;
int m;
queue<int> q;
int main(){
cin >> m;
while (m -- ){
string op;
cin >> op;
if (op == "push"){
int x;
cin >> x;
q.push(x);
}
else if(op == "pop") q.pop();
else if(op == "empty") puts(q.empty() ? "YES" : "NO");
else if(op == "query") cout << q.front() << endl;
}
return 0;
}
单调栈
AcWing 830. 单调栈
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using namespace std;
const int N = 100010;
int n;
int stk[N], sp;
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i ++ ){
int x;
cin >> x;
while (sp && stk[sp] >= x) sp -- ;
if (sp) cout << stk[sp] << ' ';
else cout << "-1 ";
stk[ ++ sp] = x;
}
return 0;
}
STL1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
using namespace std;
const int N = 100010;
int n;
stack<int> s;
int main(){
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
cin >> n;
for (int i = 0; i < n; i ++ ){
int x;
cin >> x;
while (!s.empty() && s.top() >= x) s.pop();
if (!s.empty()) cout << s.top() << ' ';
else cout << "-1 ";
s.push(x);
}
return 0;
}
单调队列
AcWing 154. 滑动窗口
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
using namespace std;
const int N = 1000010;
int n, k;
int a[N], q[N]; // 该队列维护满足单调性的最小窗口,q[hh]、q[tt]分别表示最小窗口的左右指针。
int main(){
scanf("%d%d", &n, &k);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ ){
if (hh <= tt && q[hh] < i - k + 1) hh ++ ;
while (hh <= tt && a[q[tt]] >= a[i]) tt -- ;
q[ ++ tt] = i;
if (i >= k - 1) printf("%d ", a[q[hh]]); // 当原窗口终点到达起始状态时开始
}
puts("");
hh = 0, tt = -1;
for (int i = 0; i < n; i ++ ){
if (hh <= tt && q[hh] < i - k + 1) hh ++ ;
while (hh <= tt && a[q[tt]] <= a[i]) tt -- ;
q[ ++ tt] = i;
if (i >= k - 1) printf("%d ", a[q[hh]]);
}
puts("");
return 0;
}
STL1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
using namespace std;
const int N = 1000010;
int n, k;
int a[N];
deque<int> q;
int main(){
scanf("%d%d", &n, &k);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
for (int i = 0; i < n; i ++ ){
if (!q.empty() && q.front() < i - k + 1) q.pop_front();
while (!q.empty() && a[q.back()] >= a[i]) q.pop_back();
q.push_back(i);
if (i >= k - 1) printf("%d ", a[q.front()]); // 当原窗口终点到达起始状态时开始
}
puts("");
q = deque<int>();
for (int i = 0; i < n; i ++ ){
if (!q.empty() && q.front() < i - k + 1) q.pop_front();
while (!q.empty() && a[q.back()] <= a[i]) q.pop_back();
q.push_back(i);
if (i >= k - 1) printf("%d ", a[q.front()]);
}
puts("");
return 0;
}
KMP
AcWing 831. KMP字符串
j就像是在p串上往回凿一个点然后把p往前拖1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
using namespace std;
const int N =100010, M = 1000010;
int n, m;
char s[M], p[N];
int nxt[N];
int main(){
cin >> n >> p + 1 >> m >> s + 1;
for (int i = 2, j = 0; i <= n; i ++ ){ // 第一个字符都匹不上时就是退无可退,不管它,就让它为0
while (p[i] != p[j + 1] && j) j = nxt[j];
if (p[i] == p[j + 1]) j ++ ;
nxt[i] = j;
}
for (int i = 1, j = 0; i <= m; i ++ ){
while (s[i] != p[j + 1] && j) j = nxt[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == n){
printf("%d ", i - n + 1 - 1);
j = nxt[j];
}
}
return 0;
}
这个没有错位的版本我比较喜欢hh
好吧,这个版本nxt数组的获得与使用我不是很懂,看来把比较的思路扭回来,那倒回的思路就得扭过去。
还是理解y总的吧,y总nxt数组的使用就是:
若两个比较的字符不相等,且j可以倒回(j != 0),那j这一处就应该倒回到nxt[j],所以j = nxt[j]。
j代表已匹配上的串的结束下标,0用来判断是否退无可退。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
using namespace std;
const int N = 100010, M = 1000010;
int n, m;
char p[N], s[M];
int nxt[N];
int main(){
cin >> n >> p >> m >> s;
for (int i = 1, j = 0; i < n; i ++ ){
while (p[i] != p[j] && j) j = nxt[j - 1];
if (p[i] == p[j]) j ++ ;
nxt[i] = j;
}
for (int i = 0, j = 0; i < m; i ++ ){
while (s[i] != p[j] && j) j = nxt[j - 1];
if (s[i] == p[j]) j ++ ;
if (j == n){
printf("%d ", i - n + 1);
j = nxt[j - 1];
}
}
return 0;
}
Trie
AcWing 835. Trie字符串统计
1 |
|
AcWing 143. 最大异或对
这题整明白要考啥之后其实比上一题简单,上一题是不定深度多叉树,这题是固定深度二叉树。
总之,就是遍历每个数,尝试着找与这个数具有最大海明距离的数,意思就是每一位能取反就取反,因为:
- 如果可以找到这一位取反后的位,那么在异或后这一位就会得到1,
res += 1 << i - 如果找不到这一位取反后的位,那么在异或后这一位就会得到0,
res += 0 << i(可省略)
这样就会得到该数和使其具有最大海明距离的数组成的的最大异或对及其进行异或运算的结果,然后只需打擂得到最大异或对的异或结果就可以了1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
using namespace std;
const int N = 100010, M = 3100010;
int n;
int a[N], son[M][2], idx;
void insert(int x) {
int p = 0;
for (int i = 30; i >= 0; i -- ) {
int u = x >> i & 1;
if (!son[p][u]) son[p][u] = ++ idx;
p = son[p][u];
}
}
int query(int x) {
int p = 0, res = 0;
for (int i = 30; i >= 0; i -- ) {
int u = x >> i & 1;
if (son[p][!u]) {
res += 1 << i;
p = son[p][!u];
}
else {
res += 0 << i;
p = son[p][u];
}
}
return res;
}
int main() {
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) {
scanf("%d", &a[i]);
insert(a[i]);
}
int res = 0;
for (int i = 0; i < n; i ++ ) res = max(res, query(a[i]));
printf("%d", res);
return 0;
}并查集
AcWing 836. 合并集合
1 |
|
AcWing 837. 连通块中点的数量
按秩合并就只有一句hh~1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
using namespace std;
const int N =100010;
int n, m;
int p[N], sz[N];
int find(int x) {
return p[x] == x ? x : p[x] = find(p[x]);
}
void unn(int a, int b) {
int aa = find(a), bb= find(b);
if (aa != bb) {
if (sz[aa] > sz[bb]) swap(aa, bb); // 按秩合并
p[aa] = bb;
sz[bb] += sz[aa];
}
}
int main(){
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) {
p[i] = i;
sz[i] = 1;
}
while (m -- ) {
char op[3];
int a, b;
scanf("%s", &op);
if (op[0] == 'C') {
scanf("%d%d", &a, &b);
unn(a,b);
}
else if (op[1] == '1') {
scanf("%d%d", &a, &b);
puts(find(a) == find(b) ? "Yes" : "No");
}
else if (op[1] == '2') {
scanf("%d", &a);
printf("%d\n", sz[find(a)]);
}
}
return 0;
}
AcWing 240. 食物链
按我理解这就是一个带权并查集,权重为到根节点的距离,通过距离判断“吃”关系时用到了一些数论知识(感谢信安数学)
“吃”关系的构建过程大概为每次通过给出一个“圆杠圆”结构,下圆吃上圆,把这个结构不停叠加到树上即可,但真正重要的是权重不是结构,所以可以采用路径压缩破坏结构,但一定要计算新权重。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
using namespace std;
const int N = 50010;
int n, m;
int p[N], d[N]; // parent[N], distance[N]
int find(int x) {
// int xx;
// return p[x] == x ? x : (xx = find(p[x]), d[x] += d[p[x]], p[x] = xx); // tips:逗号表达式优先级最低且自左向右结合
if (p[x] != x) {
int xx = find(p[x]);
d[x] += d[p[x]];
p[x] = xx;
}
return p[x];
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) p[i] = i;
int res = 0;
while (m -- ) {
int t, x, y;
scanf("%d%d%d", &t, &x, &y);
if (x > n || y > n) res ++ ;
else {
int xx = find(x), yy = find(y);
if (t == 1) {
if (xx == yy && (d[x] - d[y]) % 3) res ++ ; // d[x] === d[y] mod 3 真 "==="在此代表同余号(三等号)
else if (xx != yy){
p[xx] = yy;
d[xx] = d[y] - d[x]; // d[xx] + d[x] === d[y] mod 3 可以直接用等式满足同余式条件
}
}
else if (t == 2) {
if (xx == yy && (d[x] - d[y] - 1) % 3) res ++ ; // d[x] - 1 === d[y] mod 3 真 highlight:C++取余不采用最小非负剩余系,判断同余式最好将一侧移项为0
else if (xx != yy){
p[xx] = yy;
d[xx] = d[y] - d[x] + 1; // d[xx] + d[x] - d[y] === 1 mod 3
}
}
}
}
printf("%d", res);
return 0;
}
堆
AcWing 838. 堆排序
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
using namespace std;
const int N = 100010;
int n, m;
int h[N], sz;
void down(int u) {
int t = u;
// 后两步是上左右逐个比较打擂,不是上同时和左右比较,所以索引用t,打赢的继续跟下一个打。
if (2 * u <= sz && h[2 * u] < h[t]) t = 2 * u;
if (2 * u + 1<= sz && h[2 * u + 1] < h[t]) t = 2 * u + 1;
if (t != u) {
swap(h[u], h[t]);
down(t);
}
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]);
sz = n;
for (int i = n / 2; i; i -- ) down(i); // n / 2:从倒数第二层起,n对应高度h = $log_2^n$,那n / 2对应高度为$log_2^n$ - 1 = h - 1
while (m -- ) {
printf("%d ", h[1]);
h[1] = h[sz -- ];
down(1);
}
return 0;
}
STL 慢1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
using namespace std;
const int N = 100010;
int n, m;
priority_queue<int, vector<int>, greater<int>> q;
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) {
int x;
scanf("%d", &x);
q.push(x);
}
while (m -- ) {
printf("%d ", q.top());
q.pop();
}
return 0;
}
AcWing 839. 模拟堆
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
using namespace std;
const int N = 100010;
int n;
int h[N], hk[N], kh[N], sz; // hk:堆下标映射到输入下标 kh:输入下标映射到堆下标
void heap_swap(int a, int b) {
swap(kh[hk[a]],kh[hk[b]]), swap(hk[a], hk[b]);
// swap(hk[a],hk[b]), swap(kh[hk[a]], kh[hk[b]]); // 先改哪个都行
swap(h[a], h[b]);
}
void down(int u) {
int t = u;
if (2 * u <= sz && h[2 * u] < h[t]) t = 2 * u;
if (2 * u + 1 <= sz && h[2 * u + 1] < h[t]) t = 2 * u + 1;
if (u != t) {
heap_swap(u, t);
down(t);
}
}
void up(int u) {
while (u / 2 && h[u] < h[u / 2]) {
heap_swap(u, u / 2);
u /= 2;
}
}
int main() {
scanf("%d", &n);
int idx = 0;
while (n -- ) {
char op[5];
int k, x;
scanf("%s", &op);
if (!strcmp(op, "I")) {
scanf("%d", &x);
sz ++ , idx ++ ;
h[sz] = x;
hk[sz] = idx, kh[idx] = sz;
up(sz);
}
else if (!strcmp(op, "PM")) printf("%d\n", h[1]);
else if (!strcmp(op, "DM")) {
heap_swap(1, sz);
sz -- ;
down(1);
}
else if (!strcmp(op,"D")) {
scanf("%d", &k);
k = kh[k];
heap_swap(k, sz);
sz -- ;
down(k), up(k); // 只会执行一条
}
else if (!strcmp(op,"C")) {
scanf("%d%d", &k, &x);
k = kh[k];
h[k] = x;
down(k), up(k);
}
}
return 0;
}
哈希表
AcWing 840. 模拟散列表
开放寻址法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using namespace std;
const int N = 200003, NONE = 0x3f3f3f3f;
int n;
int h[N]; // 1 int = 4bytes
int find(int x) {
int k = (x % N + N) % N;
while (h[k] != NONE && h[k] != x) k = (k + 1) % N;
return k;
}
int main() {
scanf("%d", &n);
memset(h, 0x3f, sizeof h); // memset初始化的基本单位是byte
while (n -- ) {
char op[2];
int x;
scanf("%s%d", &op, &x);
int k = find(x);
if (*op == 'I') h[k] = x;
else if (*op == 'Q') puts(h[k] == x ? "Yes" : "No");
}
return 0;
}
拉链法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
const int N = 100003;
int n;
int h[N], e[N], ne[N], idx; // e[N]、ne[N]二者只是模拟Node,数据结构取决于如何使用这些模拟的Node
void insert(int x) {
int k = (x % N + N) % N; // highlight:C++中可将(余数 + N) % N以调整至N的最小非负剩余系
e[idx] = x;
ne[idx] = h[k];
h[k] = idx ++ ;
}
bool find(int x) {
int k = (x % N + N) % N;
for (int i = h[k]; i != -1; i = ne[i])
if (e[i] == x) return true;
return false;
}
int main() {
scanf("%d", &n);
memset(h, -1, sizeof h);
while (n -- ) {
char op[2];
int x;
scanf("%s%d", &op, &x);
if (*op == 'I') insert(x);
else if (*op == 'Q') puts(find(x) ? "Yes" : "No");
}
return 0;
}
STL 慢1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace std;
const int N = 200003, NONE = 0x3f3f3f3f;
int n;
unordered_map<int, int> mp;
int main() {
scanf("%d", &n);
while (n -- ) {
char op[2];
int x;
scanf("%s%d", &op, &x);
if (*op == 'I') mp[x] ++ ;
else if (*op == 'Q') puts(mp[x] > 0 ? "Yes" : "No");
}
return 0;
}
对常用memset的测试
1 |
|
1 | 00000000000000000000000000000000 0 |
AcWing 841. 字符串哈希
1 |
|
第三讲 搜索与图论
DFS
AcWing 842. 排列数字
1 |
|
AcWing 843. n-皇后问题
有规律的搜索1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
using namespace std;
const int N = 10;
int n;
char g[N][N];
int col[N], dg[N], udg[N]; // diagonal
void dfs(int u) {
if (u == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]); // highlight
puts("");
}
for (int i = 0; i < n; i ++ ) {
if (!col[i] && !dg[u + i] && !udg[n - i + u]) { // 用简单的几何也可以算,u + i:等边直角三角形的另一边长度u + 距纵轴距离i,n - i + u:n -(距纵轴距离i - 等边RT的另一边长度u)
g[u][i] = 'Q';
col[i] = dg[u + i] = udg[n - i + u] = true;
dfs(u + 1);
g[u][i] = '.';
col[i] = dg[u + i] = udg[n - i + u] = false;
}
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0);
return 0;
}
无规律的搜索(暴力搜索)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
using namespace std;
const int N = 10;
int n;
char g[N][N];
bool row[N], col[N], dg[N], udg[N];
void dfs(int x, int y, int s) {
// if (s > n) return ; // 我觉得只要算法是正确的,那么皇后数量就不会超过n
if (y == n) y = 0, x ++ ; // 列遍历结束
if (x == n) { // 行遍历结束
if (s == n) {
for (int i = 0; i < n; i ++ ) puts(g[i]);
puts("");
}
return ;
}
// 不放皇后
// g[x][y] = '.';
dfs(x, y + 1, s);
// 放皇后
if (!row[x] && !col[y] && !dg[y + x] && !udg[n - y + x]) {
g[x][y] = 'Q';
row[x] = col[y] = dg[y + x] = udg[n - y + x] = true;
dfs(x, y + 1, s + 1);
g[x][y] = '.';
row[x] = col[y] = dg[y + x] = udg[n - y + x] = false;
}
}
int main() {
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
g[i][j] = '.';
dfs(0, 0, 0);
return 0;
}
BFS
AcWing 844. 走迷宫
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
using namespace std;
using PII = pair<int, int>;
const int N = 110;
int n, m;
int g[N][N], d[N][N];
int hh, tt = -1;
PII q[N * N];
int bfs() {
memset(d, -1, sizeof d);
d[0][0] = 0;
q[ ++ tt] = {0, 0};
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (hh <= tt) {
auto t = q[hh ++];
for (int i = 0; i < 4; i ++ ) {
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
d[x][y] = d[t.first][t.second] + 1;
q[ ++ tt] = {x, y};
}
}
}
return d[n - 1][m - 1];
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
STL1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
using namespace std;
using PII = pair<int, int>;
const int N = 110;
int n, m;
int g[N][N], d[N][N];
queue<PII> q;
int bfs() {
memset(d, -1, sizeof d);
d[0][0] = 0;
q.push({0, 0});
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};
while (q.size()) {
auto t = q.front(); q.pop();
for (int i = 0; i < 4; i ++ ) {
int x = t.first + dx[i], y = t.second + dy[i];
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1) {
d[x][y] = d[t.first][t.second] + 1;
q.push({x, y});
}
}
}
return d[n - 1][m - 1];
}
int main() {
cin >> n >> m;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < m; j ++ )
cin >> g[i][j];
cout << bfs() << endl;
return 0;
}
AcWing 845. 八数码
1 |
|
树与图的深度优先遍历
AcWing 846. 树的重心
1 |
|
树与图的广度优先遍历
AcWing 847. 图中点的层次
模拟1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N];
int hh, tt = -1;
int q[N];
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int bfs() {
memset(d, -1, sizeof d);
q[ ++ tt] = 1;
d[1] = 0;
while (hh <= tt) {
int t = q[hh ++ ];
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] == -1) {
d[j] = d[t] + 1;
q[ ++ tt] = j;
}
}
}
return d[n];
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0; i < m; i ++ ) {
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs() << endl;
return 0;
}
STL1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N];
queue<int> q;
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int bfs() {
memset(d, -1, sizeof d);
q.push(1);
d[1] = 0;
while (q.size()) {
int t = q.front(); q.pop();
for (int i = h[t]; i != -1; i = ne[i]) {
int j = e[i];
if (d[j] == -1) {
d[j] = d[t] + 1;
q.push(j);
}
}
}
return d[n];
}
int main() {
memset(h, -1, sizeof h);
cin >> n >> m;
for (int i = 0; i < m; i ++ ) {
int a, b;
cin >> a >> b;
add(a, b);
}
cout << bfs() << endl;
return 0;
}
拓扑排序
AcWing 848. 有向图的拓扑序列
1 |
|
Dijkstra
AcWing 849. Dijkstra求最短路 I
1 |
|
关于0x3f3f3f3f
首先我们要知道,无穷大加无穷大等于无穷大
但计算机因其存储方式,很容易发生整数溢出,这在没有大整数类和自动扩容机制的C++下尤为明显。
所以我们要选取一个足够大但又不会导致相加溢出的数充当无穷大
那么0x3f == 0b0011 1111 == 0b0100 0000 - 0b10x3f + 0x3f ==0b0100 0000 - 0b1 + 0b0100 0000 == 0b1000 0000 - 0b10
没有发生溢出,满足必要性
但并没有说这个充当无穷大的值一定应为0x3f3f3f3f(充分性),所以我觉得可能是因为这个值在保证大的情况下可以加好几次
AcWing 850. Dijkstra求最短路 II
1 |
|
Bellman-Ford
AcWing 853. 有边数限制的最短路
对于获得最短路径的最终状态来说,串联没有影响。
而对于有边数限制的最短路来说,串联会导致得到的结果是不符合要求的,超过边数限制的最短路。
1 |
|
SPFA
AcWing 851. spfa求最短路
1 |
|
AcWing 852. spfa判断负环
1 |
|
Floyd
AcWing 854. Floyd求最短路
1 |
|
Prim
AcWing 858. Prim算法求最小生成树
1 |
|
Kruskal
AcWing 859. Kruskal算法求最小生成树
kruskal是并查集的一个应用
1 |
|
染色法判定二分图
AcWing 860. 染色法判定二分图
1 |
|
匈牙利算法
AcWing 861. 二分图的最大匹配
数组st在该情景下的意义可为:男生是否询问过女生1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
using namespace std;
const int N = 510, M = 100010;
int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N]; // match[i]:女生i的对象
bool query[N]; // bool st[N]; // 男生是否询问过女生
void add(int a, int b) {
e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}
int find(int x) {
for (int i = h[x]; i != -1; i = ne[i]) { // 遍历男生x的所有可联系女生
int j = e[i]; // 女生的编号j
if (!query[j]) { // 如果没询问过
query[j] = true; // 标记为询问,然后去问她
if (!match[j] || find(match[j])){ // 如果女生j没有对象,或者女生j的对象match[j]可以再找一个。 // highlight:query的作用就在这里,递归产生的find栈不会再去询问match[j]自己的对象j
match[j] = x; // 那女生j把男生x作为对象
return true; // 男生x成功找到对象(在未询问女生中)
}
}
}
return false; // 男生x没找着对象(在未询问女生中)
}
int main() {
memset(h, -1, sizeof h);
scanf("%d%d%d", &n1, &n2, &m);
for (int i = 0; i < m; i ++ ) {
int a, b;
scanf("%d%d", &a, &b);
add(a, b);
}
int res = 0;
for (int i = 1; i <= n1; i ++ ) {
memset(query, false, sizeof query); // 重复使用query,每个男生最初都没有询问过女生
if (find(i)) res ++ ;
}
printf("%d\n", res);
return 0;
}
第四讲 数学知识
质数
AcWing 866. 试除法判定质数
$d | n \iff \frac{n}{d} | n$
令我们枚举的d较小,即 $ d \leq \frac{n}{d} \iff d^2 \leq n \iff d \leq \sqrt{n} $
对应的代码就是
i <= n / ii * i <= ni <= sqrt(n)
推荐使用方式1,因为
2:当循环结束时,必然有$ i ^ 2 <= n$,$ (i + 1) ^ 2 > n $的情况,这时若$ n \approx 2^{32} - 1$(int最大值),那么$ (i + 1) ^ 2 $会溢出为负值继续循环一次,很危险。
3:函数sqrt()采用二分算法,时间复杂度为$ O(logn) $,应用它虽然减少了循环次数却也增加了单次循环时间,总时间复杂度即$ O(\sqrt{n}) * O(logn)$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using namespace std;
int n;
bool is_prime(int x)
{
if (x < 2) return false;
for (int i = 2; i <= x / i; i ++ )
if (x % i == 0) return false;
return true;
}
int main()
{
cin >> n;
while (n -- )
{
int a;
cin >> a;
if (is_prime(a)) puts("Yes");
else puts("No");
}
return 0;
}
AcWing 867. 分解质因数
1 |
|
AcWing 868. 筛质数
朴素筛法:筛掉所有数的倍数,时间复杂度:$O(nlogn)$
略
Eratosthenes筛法(埃氏筛法):筛掉所有质数的倍数,时间复杂度:$O(nloglogn) \approx O(n)$,
Eratosthenes筛法的一种证明:由算数基本定理:每个大于1的自然数,要么本身就是质数,要么可以写为2个或以上的质数的积,而且这些质因子按大小排列之后,写法仅有一种方式。那么所有大于1的自然数可以划分为两个集合:质数集合、以质数为因数的集合,那么我们把质数的倍数筛掉后就不存在以质数为因数的集合了。>=2的自然数集都可以这么筛,那2~n的集合自然也可以这么筛。
线性筛法(欧拉筛法):在线性时间内筛出素数。每个合数只被其最小质因子筛掉1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using namespace std;
const int N = 1000010;
int n;
int primes[N], cnt;
bool st[N]; // 0:没被筛过 1:被筛过
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
if (!st[i])
{
primes[cnt ++ ] = i;
for (int j = i + i; j <= n; j += i) st[j] = true;
}
}
int main()
{
cin >> n;
get_primes(n);
// for (int i = 0; i < cnt; i ++ ) cout << primes[i] << ' ';
// cout << endl;
cout << cnt;
return 0;
}
约数
AcWing 869. 试除法求约数
$1 \sim n$中所有约数的个数 = $ \frac{n}{1} + \frac{n}{2} + \dots + \frac{n}{n} = nlogn $,那么每个数的平均约数个数 = $ logn $
那么对每个的约数排序的时间复杂度为$O(logn * log(logn))(sort部分) < O(\sqrt n)(for部分)$
那么该组合算法的时间复杂度$O(\sqrt n)$
本题数据量为:$n\sqrt a = 100 \sqrt {2 10 ^ 9} \approx 100 4万 = 400 万 < 1亿$
4万 ^ 2 = 1.6 10 ^ 9,
5万 ^ 2 = 2.5 10 ^ 91
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
using namespace std;
int n;
vector<int> get_divisors(int n)
{
vector<int> res;
for (int i = 1; i <= n / i; i ++ )
if (n % i == 0)
{
res.push_back(i);
if (i != n / i) res.push_back(n / i);
}
sort(res.begin(), res.end());
return res;
}
int main()
{
cin >> n;
while (n -- )
{
int x;
cin >> x;
auto ans = get_divisors(x);
for (auto i : ans) cout << i << ' ';
cout << endl;
}
return 0;
}
AcWing 870. 约数个数
由算数基本定理:
设 $d$ 是 $N$ 的约数,则
他们具有相同的质因子 $q _ i$ ,且 $ 0 \leq \beta_i \leq \alpha_i$
那么 $ N $ 的因数个数,即d的数量为
另外:在int范围内,约数个数最多的数大概有1500个约数,也就是说int范围每个数的约数个数都不超过15001
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
using namespace std;
using LL = long long;
const int N = 110, MOD = 1e9 + 7;
int n;
unordered_map<int, int> alphas;
int main()
{
cin >> n;
while (n -- )
{
int a;
cin >> a;
for (int i = 2; i <= a / i; i ++ )
while (a % i == 0)
{
a /= i;
alphas[i] ++ ;
}
if (a > 1) alphas[a] ++ ;
}
LL res = 1;
for (auto a : alphas) res = res * (a.second + 1) % MOD;
printf("%lld\n", res);
return 0;
}
AcWing 871. 约数之和
接上题,将 $N$ 的约数 $d$ 每一项的可能值( $ \beta _ i $ 从 $ 0 $ 遍历至 $ \alpha _ i $)写成和式再积起来即可
1 |
|
AcWing 872. 最大公约数
$(a, b) = (b, a\ mod\ b)$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace std;
int n;
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int main()
{
scanf("%d", &n);
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", gcd(a,b));
}
return 0;
}
欧拉函数
AcWing 873. 欧拉函数
1 |
|
AcWing 874. 筛法求欧拉函数
1 |
|
快速幂
AcWing 875. 快速幂
1 |
|
AcWing 876. 快速幂求逆元
1 |
|
扩展欧几里得算法
AcWing 877. 扩展欧几里得算法
1 |
|
AcWing 878. 线性同余方程
令 $ y = -y $
由扩展欧几里得可以求得:
由贝祖定理:
若 $x$, $y$ 有解,则$ d | b $
那么只需将等式$(3)$乘$ \frac{b}{d} $,变为
此时由 $(2)$ $(4)$ 同构,可得
虽然直接这样写会WA,但是在数学上是正确的。
错误的原因在于我们的答案在LL范围内,而题目要求“输出答案必须在 $int$ 范围之内”,我们可以 $ \% m $ 直接把答案压到最小剩余系范围内,这样就一定在int范围内了
1 |
|
中国剩余定理
AcWing 204. 表达整数的奇怪方式
注意本题输入顺序及表达(与一般表示相反)!先输入模数再输入同余数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
using namespace std;
using LL = long long;
const int N = 30;
int n;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
if (b)
{
LL d = exgcd(b, a % b, y, x);
y -= a / b * x;
return d;
}
else
{
x = 1, y = 0;
return a;
}
}
int main()
{
scanf("%d", &n);
LL x = 0;
LL m1, a1;
scanf("%lld%lld", &m1, &a1);
for (int i = 0; i < n - 1; i ++ )
{
LL m2, a2;
scanf("%lld%lld", &m2, &a2);
LL k1, k2;
LL d = exgcd(m1, m2, k1, k2); // k1:“gcd方程”特解
if ((a2 - a1) % d)
{
x = -1;
break;
}
k1 *= (a2 - a1) / d; // k1:原方程特解
LL t = m2 / d;
k1 = (k1 % t + t) % t; // k1:原方程最小非负解
x = k1 * m1 + a1; // x:原方程组最小非负解
LL m = m1 / d * m2; // lcm
a1 = k1 * m1 + a1;
m1 = m;
}
if (x != -1) x = (a1 % m1 + m1) % m1;
printf("%lld\n", x);
return 0;
}
高斯消元
AcWing 883. 高斯消元解线性方程组
1 |
|
AcWing 884. 高斯消元解异或线性方程组
({0, 1}, ^)群,在{0, 1}域下,^等价于+,&等价于*1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
using namespace std;
const int N = 110;
int n;
int a[N][N];
int gauss()
{
int c, r;
for (c = 0, r = 0; c < n; c ++ )
{
int t = r;
for (int i = r; i < n; i ++ )
if (a[i][c])
t = i;
if (a[t][c] == 0) continue;
for (int i = c; i <= n; i ++ ) swap(a[t][i], a[r][i]);
for (int i = r + 1; i < n; i ++ )
if (a[i][c]) // 首一,需要消掉本行1后的元素
for (int j = c; j <= n ; j ++ )
a[i][j] ^= a[r][j];
r ++ ;
}
if (r < n) // 秩小于行数
{
for (int i = r; i < n; i ++ )
if (a[i][n]) // 0 0 ... 0 1
return 2;
return 1;
}
for (int i = n - 1; i >= 0; i -- )
for (int j = i + 1; j < n; j ++ )
a[i][n] ^= a[j][n] & a[i][j];
return 0;
}
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n + 1; j ++ )
scanf("%d", &a[i][j]);
int t = gauss();
if (t == 2) puts("No solution");
else if (t == 1) puts("Multiple sets of solutions");
else if (t == 0) for (int i = 0; i < n; i ++ ) printf("%d\n", a[i][n]);
return 0;
}
求组合数
AcWing 885. 求组合数 I
从a中元素选b个元素 等价于
- 某个元素被选中,接着从剩余a-1个中选取b-1个
- 某个元素未被选中,接着从剩余a-1个钟选取b个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
using namespace std;
const int N = 2010, MOD = 1e9 + 7;
int n;
int c[N][N];
void init()
{
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % MOD;
}
int main()
{
scanf("%d", &n);
init();
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", c[a][b]);
}
return 0;
}AcWing 886. 求组合数 II
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
using namespace std;
using LL = long long;
const int N = 100010, mod = 1e9 +7;
int n;
int fact[N], infact[N]; // factorial, inverse element of factorial
// 只要两个10^9相乘就要转LL防止爆int
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
k >>= 1;
a = (LL)a * a % p;
}
return res;
}
int main()
{
scanf("%d", &n);
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
while (n -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", (LL)fact[a] * infact[b] % mod * infact[a - b] % mod);
}
return 0;
}AcWing 887. 求组合数 III
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
using namespace std;
using LL = long long;
int n;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
k >>= 1;
a = (LL)a * a % p;
}
return res;
}
int C(int a, int b, int p)
{
if (b > a) return 0;
int res = 1;
for (int i = b, j = a;i >= 1; i -- , j -- )
{
res = (LL)res * j % p;
res = (LL)res * qmi(i, p - 2, p) % p;
}
return res;
}
int lucas(LL a, LL b, int p)
{
if (a < p && b < p) return C(a, b, p);
return (LL)lucas(a / p, b / p, p) * C(a % p, b % p, p) % p; // highlight:这里要递归使用lucas's Theorem以完全分解至p进制!
}
int main()
{
scanf("%d", &n);
while (n -- )
{
LL a, b;
int p;
scanf("%lld%lld%d", &a, &b, &p);
printf("%d\n", lucas(a, b, p));
}
return 0;
}AcWing 888. 求组合数 IV
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
using namespace std;
const int N = 5010;
int primes[N], cnt;
bool st[N];
int sum[N];
void get_primes(int n)
{
for (int i = 2; i <= n; i ++ )
{
if (!st[i]) primes[cnt ++ ] = i;
for (int j = 0; primes[j] <= n / i; j ++ )
{
st[primes[j] * i] = true;
if (i % primes[j] == 0) break;
}
}
}
int get(int x, int p)
{
int res = 0;
while (x)
{
res += x / p;
x /= p;
}
return res;
}
vector<int> mul(vector<int> &A, int b)
{
vector<int> res;
for (int i = 0, t = 0; i < A.size() || t; i ++ )
{
if (i < A.size()) t += A[i] * b;
res.push_back(t % 10);
t /= 10;
}
while (res.back() == 0 && res.size() > 1) res.pop_back();
return res;
}
int main()
{
int a, b;
scanf("%d%d", &a, &b);
get_primes(a);
for (int i = 0; i < cnt; i ++ )
{
int p = primes[i];
sum[i] = get(a, p) - get(b, p) - get(a - b, p);
}
vector<int> res;
res.push_back(1);
for (int i = 0; i < cnt; i ++ )
while (sum[i] -- )
// for (int j = 0; j < sum[i]; j ++ )
res = mul(res, primes[i]);
for (int i = res.size() - 1; i >= 0; i -- ) printf("%d", res[i]);
puts("");
return 0;
}AcWing 889. 满足条件的01序列
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
using namespace std;
using LL = long long;
const int N =100010, mod = 1e9 + 7;
int n;
int qmi(int a, int k, int p)
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
k >>= 1;
a = (LL)a * a % p;
}
return res;
}
int main()
{
scanf("%d", &n);
int a = 2 * n, b = n;
int res = 1;
for (int i = b, j = a; i >= 1; i --, j -- )
{
res = (LL)res * j % mod;
res = (LL)res * qmi(i, mod - 2, mod) % mod;
}
res = (LL)res * qmi(n + 1, mod - 2, mod) % mod;
printf("%d\n", res);
return 0;
}容斥原理
AcWing 890. 能被整除的数
容斥原理应用,见得少真的想不到呜呜呜1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
using namespace std;
using LL = long long;
const int N = 20;
int n, m;
int p[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < m; i ++ ) scanf("%d", &p[i]);
int res = 0;
for (int i = 1; i < 1 << m; i ++ ) // 遍历2 ^ m - 1种状态(除全0,即不选集合)
{
int t = 1, cnt = 0; // t:选中集合对应质数的积,cnt:选中集合的数量
for (int j = 0; j < m; j ++ ) // 遍历i的每一位二进制数(遍历所有集合的选中状态)
if (i >> j & 1) // 若选中集合
{
if ((LL)t * p[j] > n) // 若选中集合对应质数的积大于给定整数,说明给定整数中一定没有选中集合对应质数的公倍数。
{
t = -1;
break;
}
t *= p[j];
cnt ++ ;
}
if (t != -1)
{
if (cnt & 1) res += n / t; // 若选中奇数个集合,自增
else res -= n / t; // 若选中偶数个集合, 自减
}
}
printf("%d\n", res);
return 0;
}
博弈论
AcWing 891. Nim游戏
1 |
|
AcWing 892. 台阶-Nim游戏
对于这种问题,可以先模拟 $ n=1, 2, 3, 4, \dots $ 这些简单情况,然后大胆推理(好吧其实我不知道还有什么别的办法)
$n = 1$时:先手直接将第 $1$ 级台阶上的石子 $a_1$ 拿到第 $0$ 级,先手必胜。
$n = 2$时,先手在某一步:
- 若 $a_1 = 0$ ,
若 $a_2 = 0$,先手败。
若 $a_2 \neq 0$ ,先手只能将 $a_2$ 减少,$ a_1 $增加,敌手只需不停重复 $n = 1$的情况即可让先手败。 - 若 $a_1 \neq 0$ ,
若 $a_2 = 0$,先手做 $n = 1$ 时情况,先手胜
若 $a_2 \neq 0$ ,先手做 $n = 1$ 时情况,让敌手进入 $a_1 = 0, a_2 \neq 0$的情况,敌手必败,先手必胜。
1 |
|
AcWing 893. 集合-Nim游戏
1 |
|
AcWing 894. 拆分-Nim游戏
和上一题最大的区别是每个新状态不再是单个状态的sg值,而是拆分出的两个子状态的sg异或和(SG原理)。
因为两堆石子无序,所以我们假设第一堆大于等于第二堆,枚举所有可能的新状态(两个拆分子状态),然后将其sg异或和插入集合。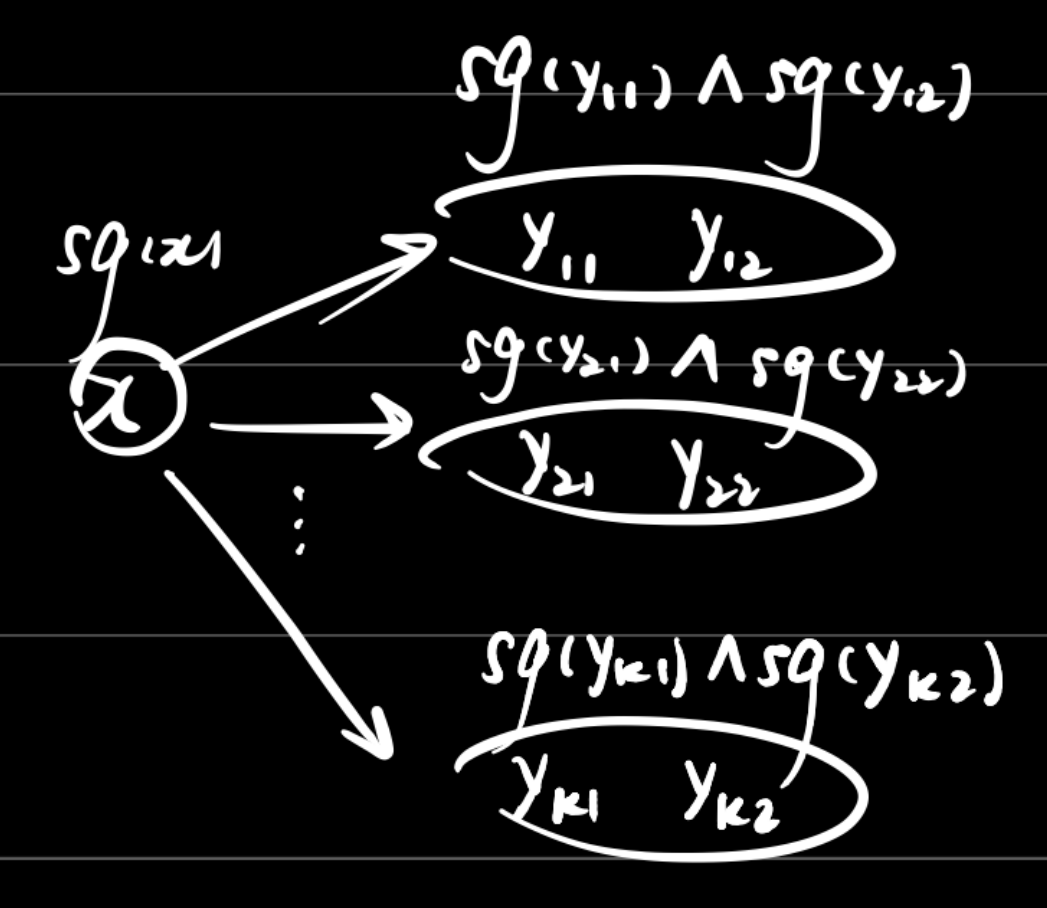
1 |
|
第五讲 动态规划
背包问题
Acwing 2. 01背包问题
朴素版:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
}
printf("%d\n", f[n][m]);
return 0;
}
空间优化版(滚动数组):
改写思路:
- 将f声明为一维数组
- 将f曾经的第一纬度删掉,此时赋值号右侧为”上层”,左侧为”本层”
- 去除
f[j] = f[j]恒等式,将if (j >= v[i])整合进第二层for循环 - 若从左向右更新,当更新右侧格子时,左边格子已经被更新为本层格子而非上层格子,所以将第二层
for循环改为从右向左更新1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++ )
for (int j = m; j >= v[i]; j -- )
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
return 0;
}
Acwing 3. 完全背包问题
朴素版:
本题TLE
1 |
|
“就近转移”优化:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
{
f[i][j] = f[i - 1][j];
if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
printf("%d\n", f[n][m]);
return 0;
}
滚动数组优化:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
using namespace std;
const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d%d", &v[i], &w[i]);
for (int i = 1; i <= n; i ++ )
for (int j = v[i]; j <= m; j ++ )
f[j] = max(f[j], f[j - v[i]] + w[i]);
printf("%d\n", f[m]);
return 0;
}
Acwing 4. 多重背包问题
注意:这里有三重循环,分别是
物品序号——当前容量——物品件数
当物品件数变多时,其单独作为一重循环会极大地增加时间复杂度,
所以在多包2中,我们将每个物品构造成$logs$个物品,他们的体积和价值的系数(件数)呈指数序列$1, 2, 4, 8, \dots, k, c$(最后两项我还没想出来怎么用数学语言表述),本质上就是将其二进制表示然后计算其位权,最后若不能恰好表示则有剩余件数c
这样我们就用空间换时间,将其变为了01背包问题,去除了最后一重循环,但第一重循环的范围从$N$增加为$NlogS$
总时间复杂度由 $O(n \cdot m \cdot s)$ 变为 $O(nlogs \cdot m)$
朴素版:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
const int N = 110;
int n, m;
int v[N], w[N], s[N];
int f[N][N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d%d%d", &v[i], &w[i], &s[i]);
for (int i = 1; i <= n; i ++ )
for (int j = 0; j <= m; j ++ )
for (int k = 0; k <= s[i] && k * v[i] <= j; k ++ )
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
printf("%d\n", f[n][m]);
return 0;
}
Acwing 5. 多重背包问题 II
优化思路写在上一题和朴素做法做对比了
空间换时间,位优化版:
1 |
|
Acwing 9. 分组背包问题
1 |
|
线性DP
Acwing 898. 数字三角形
1 |
|
Acwing 895. 最长上升子序列
不记录转移1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
using namespace std;
const int N = 1010;
int n;
int a[N], f[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ )
{
f[i] = 1;
for (int j = 1; j <= i; j ++ )
if (a[j] < a[i])
f[i] = max(f[i], f[j] + 1);
}
int res = 0;
for (int i = 1; i <= n; i ++ )
res = max(res, f[i]);
printf("%d\n", res);
return 0;
}
记录转移1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
using namespace std;
const int N = 1010;
int n;
int a[N], f[N], g[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ )
{
f[i] = 1;
for (int j = 1; j <= i; j ++ )
if (a[j] < a[i])
if (f[i] < f[j] + 1)
{
f[i] = f[j] + 1;
g[i] = j;
}
}
int k = 1;
for (int i = 1; i <= n; i ++ )
if (f[k] < f[i])
k = i;
printf("%d\n", f[k]);
for (int i = 0, len = f[k]; i < len; i ++)
{
printf("%d ", a[k]);
k = g[k];
}
return 0;
}
Acwing 896. 最长上升子序列 II
用了和yls相同的思路,但是二分部分采用了lower_bound
向量q的定义是:长度为i的严格递增子串中,末尾元素最小为q[i]
这样的向量q一定是严格递增的,因为若q[i] >= q[i + 1],那么q[i + 1]所对应的长度为i + 1的子串的前i个元素所形成的子串的末尾元素 < q[i] < q[i + 1],与定义矛盾。
所以新进来的元素要么加在末尾(接在目前最长的递增子串后),要么替代第一个大于等于它的元素(更新满足q定义的递增子串的末尾),这里的思想是贪心:对于同样长度的子串,它的末尾元素越小越好,这样它才有机会接上更多的元素。
1 |
|
Acwing 897. 最长公共子序列
1 |
|
Acwing 902. 最短编辑距离
这道题对我而言,lc官方的视频题解更好理解,学习要获取多方资源才行。
状态表示:f[i][j]表示将a[1 .. i]和b[1 .. j]整相等所需要的最小操作数。
状态计算:
当遍历到某个f[i][j]时,两段文本的末尾元素有两种情况:
- $a[i] = b[j]$,这时不需要操作这两段文本的末尾元素,直接从他们的前一个转移即可(只要把前面那两段整相等了,那么这两段无需操作自然相等),
f[i][j] = f[i - 1][j - 1] - $a[i] \neq b[j]$,我们可以进行三种操作,这三种操作分别是:
- 删除:操作1次,将a的末尾元素
a[i]删除,然后把a[1 .. i - 1]和b[1 .. j]整成相等的,这步所需要的最小操作数为f[i - 1][j],f[i][j] = 1 + f[i - 1][j] - 插入:操作1次,在a的末尾元素后插入插入一个新元素
a[i + 1] = b[j],这样我们就可以像情况1那样不考虑这两个末尾元素,而是考虑子结构a[1 .. i]和b[1 .. j - 1],这步所需要的最小操作数为f[i][j - 1],f[i][j] = 1 + f[i][j - 1] - 替换:操作1次,将a的末尾元素
a[i]替换为b[j],同样地,就可以不考虑这两个末尾元素,而是考虑子结构a[1 .. i - 1]和b[1 .. j - 1],这步所需要的最小操作数为f[i - 1][j - 1],f[i][j] = 1 + f[i - 1][j - 1]
可以看出这三种情况都是先进行了1步操作,然后再进行将子结构整相等的操作。
因此我们可以写出这样的状态转移方程:
注意到这里存在[i - 1]这种字样,谨记yxc老师说的,这种情况我们的存储和循环都要从1起,同时要对0行、0列进行初始化1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
using namespace std;
const int N = 1010;
int n, m;
char a[N], b[N];
int f[N][N];
int main()
{
scanf("%d%s", &n, a + 1);
scanf("%d%s", &m, b + 1);
for (int i = 1; i <= n; i ++ ) f[i][0] = i;
for (int j = 1; j <= m; j ++ ) f[0][j] = j;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1];
else f[i][j] = 1 + min(f[i - 1][j - 1], min(f[i - 1][j], f[i][j - 1]));
// else f[i][j] = 1 + min(f[i - 1][j - 1], f[i - 1][j], f[i][j - 1]);
}
printf("%d\n", f[n][m]);
return 0;
}
Acwing 899. 编辑距离
多次使用上一题的算法得到最短编辑距离然后比较、计数即可。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
using namespace std;
const int N = 20, M = 1010;
int n, m;
char str[M][N];
int f[N][N];
int min_edit_distance(char a[], char b[])
{
memset(f, 0, sizeof f);
int la = strlen(a + 1), lb = strlen(b + 1);
for (int i = 0; i <= la; i ++ ) f[i][0] = i;
for (int j = 0; j <= lb; j ++ ) f[0][j] = j;
for (int i = 1; i <= la; i ++ )
for (int j = 1; j <= lb; j ++ )
if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1];
else f[i][j] = 1 + min(f[i - 1][j], min(f[i][j - 1], f[i - 1][j - 1]));
return f[la][lb];
}
int main()
{
scanf("%d%d", &n, &m);
for (int i = 0; i < n; i ++ ) scanf("%s", str[i] + 1);
while (m -- )
{
char tar[N]; // target
int ub; // upperbound
scanf("%s%d", tar + 1, &ub);
int res = 0;
for (int i = 0; i < n; i ++ )
if (min_edit_distance(str[i], tar) <= ub) res ++ ;
printf("%d\n", res);
}
return 0;
}
区间DP
Acwing 282. 石子合并
1 |
|
计数类DP
Acwing 900. 整数划分
这种dp是在其他dp的基础上,计算所有转移的方案数,所以转移方程的形式是 $’+’$ 而不是 $’max’$ 或 $’min’$。
完全背包dp+计数
状态表示(最优子结构):f[i][j]:在1 .. i中选,且总和为j的方案的数
状态转移:
由1
2f[i][j] = f[i - 1][j] + f[i - 1][j - i] + f[i - 1][j - i * 2] + ... + f[i - 1][j - i * s]
f[i][j - i] = f[i - 1][j - i] + f[i - 1][j - i * 2] + ... + f[i - 1][j - i * s]
可得f[i][j] = f[i - 1][j] + f[i][j - i]
采用滚动数组后:f[j] = f[j] + f[j - i]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N];
int main()
{
scanf("%d", &n);
f[0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = i; j <= n; j ++ )
f[j] = (f[j] + f[j - i]) % mod;
printf("%d\n", f[n]);
return 0;
}
其他dp+计数:
状态表示:f[i][j]:总和为i,且由j个数表示的方案的数
状态转移:
f[i][j]的最小数是1:将这个最小数1减去,其对应方案数f[i - 1][j - 1]f[i][j]的最小数大于1:将所有数减去1,其对应方案数f[i - j][j]
转移的状态不重不漏,故f[i][j] = f[i - 1][j - 1] + f[i - j][j]
结果表示:
总方案数即为总和为n,且由任意个数表示的方案,即f[n][1] + f[n][2] + ... + f[n][n]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n;
int f[N][N];
int main()
{
scanf("%d", &n);
f[0][0] = 1;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= i; j ++ )
f[i][j] = (f[i - 1][j - 1] + f[i - j][j]) % mod;
int res = 0;
for (int i = 1; i <= n; i ++ ) res = (res + f[n][i]) % mod;
printf("%d\n", res);
return 0;
}
数位统计DP
Acwing 338. 计数问题
大无语题1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
using namespace std;
int a, b;
int get_sz(int n)
{
int res = 0;
while (n)
{
res ++ ;
n /= 10;
}
return res;
}
int count(int n, int x)
{
int res = 0;
int sz = get_sz(n);
// 设整数为abc d efg, d为当前遍历到的数,下标为i
for (int i = 1; i <= sz; i ++ )
{
int p = pow(10, i - 1); // p为efg这几位所能形成的最大值(用来切掉efg段用的)
int dl = n / p /10, di = n / p % 10, dr = n % p;
// digit_l:切掉efg段得abcd,再切掉1个10进制位得abc
// digit_i:切掉efg段得abcd,取最后1个十进制位得成d
// digit_r:取efg段得efg
// 000 < abc段 <= abc - 1
if (x) res += dl * p; // x != 0,那么abc段遍历000 .. abc-1,efg段遍历000 .. 999,做笛卡尔积得到abc*1000种方案
else if (!x && dl) res += (dl - 1) * p; // x == 0 且 abc段 != 0,那么abc段遍历001 .. abc-1(没有0000efg这种表示方法),efg段遍历000 .. 999,做笛卡尔积得到(abc - 1) * 1000种方案
// abc段 == abc
if (di > x && (x || dl)) res += p; // 第i位数di > x, 那么abc段 = abc, efg段遍历000 .. 999, 做笛卡尔积得到1 * 1000种方案
else if (di == x && (x || dl)) res += dr + 1; // 第i位数di == x, 那么abc段 = abc,efg段遍历000 .. efg,做笛卡尔积得到1 * (efg + 1)种方案
// 记得限制abc和d不能同时为0
}
return res;
}
int main()
{
while (scanf("%d%d", &a, &b), a || b)
{
if (a > b) swap(a, b);
for (int i = 0; i <= 9; i ++ )
printf("%d ", count(b, i) - count(a - 1, i));
puts("");
}
return 0;
}
状态压缩DP
Acwing 291. 蒙德里安的梦想
这种问题将所有状态压缩为数,一定要分清各个数据结构的维度是状态还是行列!1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
using namespace std;
using LL = long long;
const int N = 12, M = 1 << N;
int n, m;
LL f[N][M]; // f[i][j]含义:第i列,状态为j时的可行状态数
bool st[M]; // state1
vector<int> state[M]; // state2,state[i][j]:某列状态为i时,其前一列的可行状态j
int main()
{
while (cin >> n >> m, n || m)
{
// 预处理可行状态state1(满足奇偶关系)
for (int i = 0; i < 1 << n; i ++ ) // 所有状态
{
int cnt = 0; // 每个0段的大小
bool is_valid = true; // 假设状态i有效
for (int j = 0; j < n; j ++ ) // 用j遍历状态i的每一位数
if (i >> j & 1) // i的第j个数为1
{
if (cnt & 1) // 第j个数前面的0段为奇数段
{
is_valid = false; // 状态i不行
break; // 不用看了
}
else cnt = 0; // 第j个数前面的0段为偶数段。目前可行,接着遍历,对下个0段重新计数
}
else cnt ++ ; // i的第j个数为0,0段大小加1
if (cnt & 1) is_valid = false; // 特判最后一个0段,因为它后面没有1
st[i] = is_valid; // 将该状态记录进state1
}
// 预处理可行状态state2(满足冲突关系)
for (int i = 0; i < 1 << n; i ++ ) // 第i列起始小格的状态
{
state[i].clear(); // 清空,准备装入可行状态
for (int j = 0; j < 1 << n; j ++ ) // 第i - 1列插进来的小长方形
if ((i & j) == 0 && st[i | j]) // 两相邻列无交集(不冲突)且第i - 1列插进来后满足奇偶关系
state[i].push_back(j); // 装入i的可行状态的前一列的可行状态
}
// 动态规划
memset(f, 0, sizeof f);
f[0][0] = 1;
for (int i = 1; i <= m; i ++ ) // 第i列
for (int j = 0; j < 1 << n; j ++ ) // 第i列的状态j
for (auto k : state[j]) // 当第i列状态为j时,i - 1列的可行状态k
f[i][j] += f[i - 1][k]; // 把前一列每个可行状态的方案数加入本列本状态的方案数。
cout << f[m][0] << endl; // 下标为m且没有插到棋盘外的方案数即为最终答案(第一维下标应为0 .. m - 1)
}
return 0;
}
Acwing 91. 最短Hamilton路径
本题应将状态(走过路径)压缩至第一维度1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
using namespace std;
const int N = 21, M = 1 << N;
int n;
int w[N][N];
int f[M][N];
int main()
{
cin >> n;
for (int i = 0; i < n; i ++ )
for (int j = 0; j < n; j ++ )
cin >> w[i][j];
memset(f, 0x3f, sizeof f);
f[1][0] = 0; // 初始状态在点0,故第0位是00...01 = 1,第一维度为1,第二维度是0
for (int i = 0; i < 1 << n; i ++ ) // 枚举所有状态
for (int j = 0; j < n; j ++ ) // 对每个状态枚举所有点j
if (i >> j & 1) // 找到一个走过的点j
for (int k = 0; k < n; k ++ ) // 枚举点j的上一点k
if (i >> k & 1) // 找到一个走过的点k
f[i][j] = min(f[i][j], f[i - (1 << j)][k] + w[k][j]); //更新经点k走到点j的最短路径的距离(先将点j对应的二进制位减去,代表当前路只走到k的状态,然后获取距离、加上k -> j的距离,然后打擂)
cout << f[(1 << n) - 1][n - 1] << endl; // 选出Hamilton路径,即状态为全1,即(1 << n) - 1、重点为n - 1的路径
return 0;
}
树形DP
Acwing 285. 没有上司的舞会
1 |
|
记忆化搜索
Acwing 901. 滑雪
1 |
|
第六讲 贪心
区间问题
AcWing 905. 区间选点
贪心策略:
- 将所有区间按右端点非降序排序
- 遍历所有区间
- 若当前区间中已包含点,pass
- 若当前区间不包含点,在其右端点加一个点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
using namespace std;
const int N = 100010, INF = 0x3f3f3f3f;
int n;
struct Range
{
int l, r;
bool operator< (const Range &W) const
{
return r < W.r;
}
}range[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
range[i] = {a, b};
}
sort(range, range + n);
int res = 0;
int ed = -INF; // 当前最优区间(右端点被尽可能多的区间包含的区间)的右端点,同时也是最新加的点的坐标
for (int i = 0; i < n; i ++ )
{
Range rg = range[i];
if (ed < rg.l)
{
res ++ ; // 加入一个点
ed = rg.r; // 将该区间选为最优区间,更新最优右端点
}
}
printf("%d\n", res);
return 0;
}
AcWing 908. 最大不相交区间数量
1 |
|
AcWing 906. 区间分组
1 |
|
AcWing 907. 区间覆盖
贪心策略:
- 将所有区间按左端点非降序排序
- 遍历区间,每次:在所有能覆盖st的区间中选择右端点最大的那个区间,然后将这个右端点更新为新的st(每次都覆盖从左边st起 连续的 尽可能多的 长度)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
using namespace std;
const int N = 100010, INF = 0x3f3f3f3f;
int n;
struct Range
{
int l, r;
bool operator< (const Range& W) const
{
return l < W.l;
}
}range[N];
int main()
{
int st, ed;
scanf("%d%d", &st, &ed);
scanf("%d", &n);
for (int i = 0; i < n; i ++ )
{
int l, r;
scanf("%d%d", &l, &r);
range[i] = {l, r};
}
sort(range, range + n);
int res = 0;
bool success = false;
for (int i = 0; i < n; i ++ )
{
int j = i, r = -INF;
while (j < n && range[j].l <= st)
{
r = max(r, range[j].r);
j ++ ;
}
if (r < st) break;
res ++ ;
if (r >= ed) // 只有进入这里才是找到了
{
success = true;
break;
}
st = r;
i = j - 1;
}
if (!success) res = -1;
printf("%d\n", res);
return 0;
}
Huffman树
AcWing 148. 合并果子
这个题没有要求合并两堆的位置必须相邻,所以可以直接贪心(每次合并所需的体力最小)。另外贪心一般是局部最优解,但这个应该是全局最优解。
若要求了相邻,那么只能动态规划。
1 |
|
排序不等式
AcWing 913. 排队打水
上课讲了挺多遍,但是没有证明
当打水时间数组(非严格)单调递增时,总打水时间最小
$proof:$
假设打水时间数组不单调递增,即存在某个 $i$ 使得 $t_i > t_{i + 1}$ (单调递减)时,总打水时间更小。
那么二者之后(含)的打水总时间为
$t_{减} = t_i (n - i) + t_{i + 1} (n - i - 1)$
若将其交换,二者单调递增后,二者之后(含)的打水总时间为
$t_{增} = t_{i + 1} (n - i) + t_i (n - i - 1)$
那么:
与假设自身矛盾,故不存在$t_i > t_{i + 1}$ (单调递减)时,总打水时间最小。
$Q.E.D$
ps. 贪心算法的证明一般采用反证法、同时满足$\leq$和$\geq$、数学归纳法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
using LL = long long;
const int N = 100010;
int n;
int a[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
LL res = 0;
for (int i = 0; i < n; i ++ )
res += a[i] * (n - i - 1);
printf("%lld\n", res);
return 0;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
using LL = long long;
const int N = 100010;
int n;
int a[N];
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
sort(a + 1, a + n + 1);
LL res = 0;
for (int i = 1; i <= n; i ++ )
res += a[i] * (n - i);
printf("%lld\n", res);
return 0;
}
第二种表示方法1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
using namespace std;
using LL = long long;
const int N = 100010;
int n;
int a[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
reverse(a, a + n);
LL res = 0;
for (int i = 0; i < n; i ++ ) res += a[i] * i; // 把要等着i的人放在前面存储,这样表示方便
printf("%lld\n", res);
return 0;
}
绝对值不等式
AcWing 104. 货仓选址
中位数,考试扣了我15分的题。
排序不等式:
对于升序序列 $\\{x_i\\}$
引理:
那么:
所以,
若 $n$ 为奇数,则 $x$ 为中位数时,$d$ 最小
若 $n$ 为偶数,则 $x$ 在中位数对所形成的闭区间中时,$d$ 最小
二维最短曼哈顿距离:因坐标轴独立,故可以分别计算相加
二维最短欧几里得距离:费马点1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
using namespace std;
const int N = 100010;
int n;
int a[N];
int main()
{
scanf("%d", &n);
for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);
sort(a, a + n);
int res = 0;
for (int i = 0; i < n; i ++ ) res += abs(a[i] - a[n / 2]);
printf("%d\n", res);
return 0;
}
推公式
AcWing 125. 耍杂技的牛
推公式(感觉是猜公式hh)叠牛汉:
题目给出:
那么自然想到两个变量分别的排放顺序:
- $w$ 轻的放上面、$w$ 重的放下面
- $s$ 小的放上面、$s$ 大的放下面
那么需要找到一个公式把他们综合起来然后按其贪心。
(猜一个权重相等的形式: $w+s$,越大越往下放)
贪心策略:将所有牛按$w + s$非降序排序所得到的 最高风险值 最小
(想个办法证明它对。)
$proof:$
假设$w + s$不单调递增,即存在某个 $i$ 使得 $w_i + s_{i} > w_{i + 1} + s_{i +1} $ (单调递减)时,最大风险值更小。
那么:
| 状态\风险值\牛 | i | i + 1 |
|---|---|---|
| 交换前(降序) | $\sum_{i = 1}^{i - 1}w_i - s_i$ | $\sum_{i = 1}^{i}w_i - s_{i +1}$ |
| 交换后(升序) | $\sum_{i = 1}^{i - 1}w_i - s_{i + 1}$ | $\sum_{i = 1}^{i - 1}w_i + w_{i + 1} - s_i$ |
因我们想知道交换前后二者最大危险值的相对大小,所以可以同时先化简他们
$ - \sum_{i = 1}^{i - 1}w_i$,有:
| 状态\风险值\牛 | i | i + 1 |
|---|---|---|
| 交换前(降序) | $ - s_i$ | $w_i - s_{i +1}$ |
| 交换后(升序) | $ - s_{i + 1}$ | $w_{i + 1} - s_i$ |
$+(s_i +s_{i +1})$,有:
| 状态\风险值\牛 | i | i + 1 |
|---|---|---|
| 交换前(降序) | $ s_{i + 1}$ | $w_i + s_{i}$ |
| 交换后(升序) | $ s_{i} $ | $w_{i + 1} + s_{i +1}$ |
因为
所以
即降序的最大风险值更大,与假设矛盾。
故原命题成立
$Q.E.D$
1 |
|
