人工智能领域的一本经典教材。

作为导论，涵盖知识还是很广泛的。

绪论

略

知识表示与知识图谱

知识的概念

知识：把有关信息关联在一起所形成的信息结构

知识分为“事实”和“规则”。

相对正确性：在一定的条件及环境下，知识一般是正确的。

不确定性：知识不是“真”与“假”的二值结构，“真”与“假”间存在中间状态，“真”是有程度的。

可表示性：知识可以用适当形式表现出来。

可利用性：知识可以被利用。

知识表示：将人类知识形式化或者模型化。

一阶谓词逻辑表示法

人工智能中的逻辑分为经典命题逻辑和一阶谓词逻辑。

命题（proposition）：一个非真即假的陈述句。通常用大写的英文字母表示。

命题可以在一种条件下为真，在另一种条件下为假。

按抽象与否，命题分为命题常量与命题变元，命题变元只有把确定的命题代入后才有可能具有明确的真值。

原子命题：简单陈述句表达的命题。

复合命题：对原子命题使用连接词构成的命题。

谓词（predicate）：即谓语，分为谓词名与个体两个部分。其一般形式：

其中，P是谓词名，$x_1, x_2, \dots, x_n$是个体。

元数：谓词包含的个体数目

项：个体常量、个体变元、函数的统称

个体域：个体变元的取值范围

函数：一种一一映射，其值为个体域中的某个个体

谓词公式

连接词（按优先级顺序）

$\neg$：“非”（negation）

$\wedge$：“合取”（conjunction）

$\vee$：“析取”（disjunction）

$\rightarrow$：“蕴涵”（implication），$P\rightarrow Q$：P蕴涵Q，P称前件、Q称后件。

$\leftrightarrow$：“等价”（equivalence）

$P$ $Q$ $\neg P$ $P\vee Q$ $P\wedge Q$ $P\rightarrow Q$ $P\leftrightarrow Q$
T T F T T T T
T F F T F F F
F T T T F T F
F F T F F T T

注意：蕴涵的真值，如果前件为假，那么无法判断后件为何值时蕴涵式为假。所以前件为假时蕴涵式为真。

$\forall$：全称量词（universal quantifier）“任意”

$\exists$：存在量词（existential quantifier）“存在”

量词的辖域：量词后的整体谓词公式，辖域内与量词同名的变元称为约束变元，不同名的称为自由变元。

常用等价式

吸收律：

德摩根律：

连接词化归律：

量词转换律：

永真蕴涵

如果$P\rightarrow Q$永真，则$P\Rightarrow Q$

假言推理：又称肯定前件（Modus Ponens）

拒取式推理：又称否定后件（Modus Tollens）

（逆否后肯定前件）

假言三段论：

全称固化（全称量词消去，UI）：

存在固化（存在量词消去，EI）：

反证法：

$P\Rightarrow Q$，当且仅当$P\wedge \neg Q \Leftrightarrow F$

证明很容易，先把左边化成蕴涵。从左到右：只有P:T Q:F 左式才会F，而P:T Q:F则右侧为真，其余三种情况都为假。从右到左：则P:F Q:T，这是为真的情况。（正式的证明以后再写）

产生式表示法

确定性规则知识的产生式：

不确定性规则知识的产生式：

习题

关于习题部分，书后有详细的答案，而且较为准确，我当时写的比较潦草，所以这里只点出几个值得注意的点。下同。

2.1 (5)

答案为：

原自然语言表述：要想出国留学，必须通过外语考试。

这里的答案用了一个逆否命题的形式：如果没通过外语考试，那么不能出国留学。

第五版中2.5后新增了一道题：

2.6 用产生式表示：如果一个人发烧、呕吐、出现黄恒，那么得肝炎的可能性有7成。

确定性推理方法

推理：从已知的事实出发，通过运用已掌握的知识，找出其中蕴涵的事实，或归纳出新的事实的过程。

按推出结论的途径：

  • 演绎推理：一般到个别

  • 归纳推理：个别到一般

  • 默认推理

按推理所用的知识：

  • 确定性推理

  • 不确定性推理

按推理过程中推出的结论是否越来越接近最终目标：

  • 单调推理

  • 非单调推理

按推理中是否运用与推理有关的启发性知识：

  • 启发式推理

  • 非启发式推理

自然演绎推理

例3.1

设已知如下事实：

  1. 凡是容易的课程小王 (Wang) 都喜欢;
  2. C 班的课程都是容易的;
  3. ds是C班的一门课程。

求证：小王喜欢 ds 这门课程。

证明：

设：
$Easy(x)$：x是容易的;
$Like(y, x)$：y喜欢 x ;
$C(x)$：x是C班的一门课程。

谓词公式集：

G：

推理：

全称固化：

全称固化：

P规则、假言推理：

T规则、假言推理：

即小王喜欢ds这门课程。

谓词公式集->子句集

原子（atom）谓词公式：一个不能再分解的命题

文字（literal）：原子谓词公式及其否定

子句（clause）：文字的析取式

子句集（set of clauses）：子句构成的集合

空子句（拉丁语nihil）：NIL，不含任何文字的子句。NIL是永假的，不可满足的

转换步骤：

例3.2

将下列谓词公式化为子句集

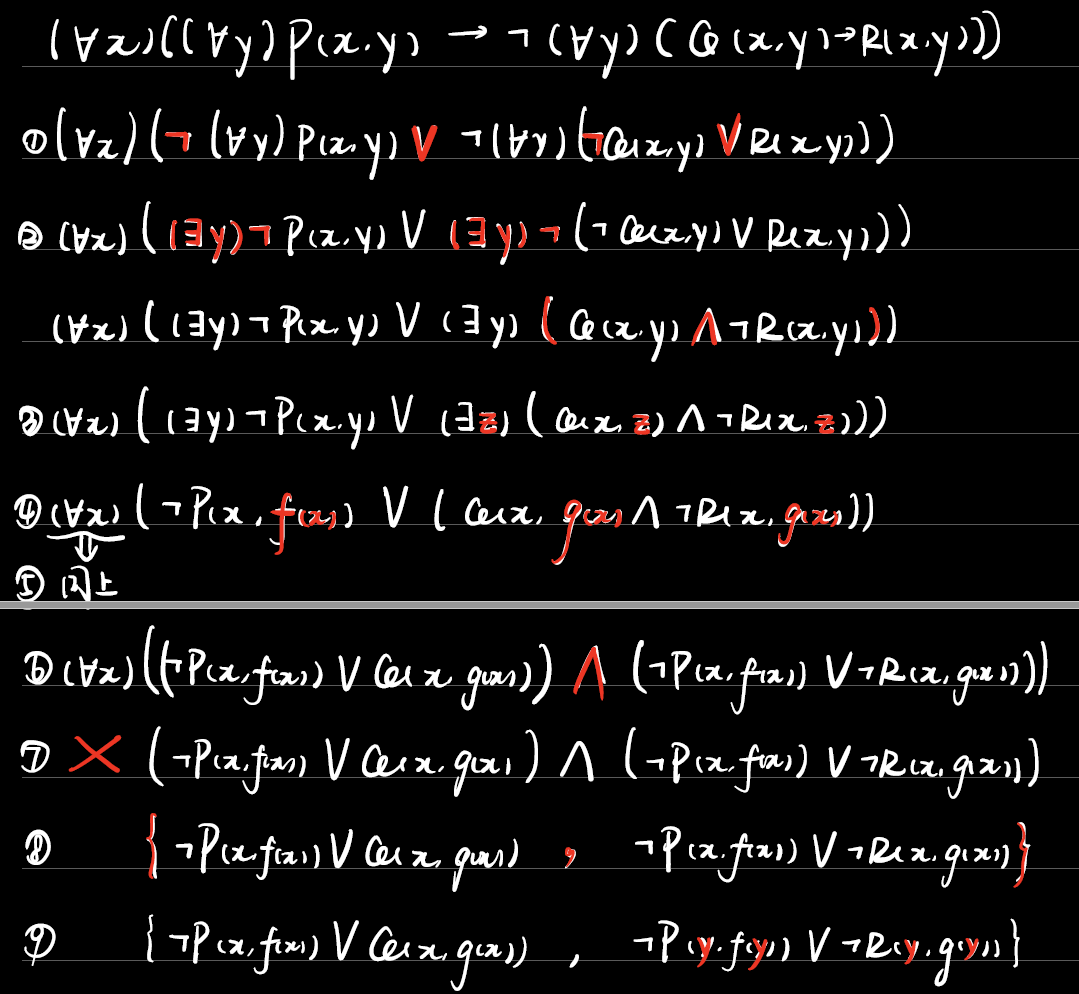
例3.3

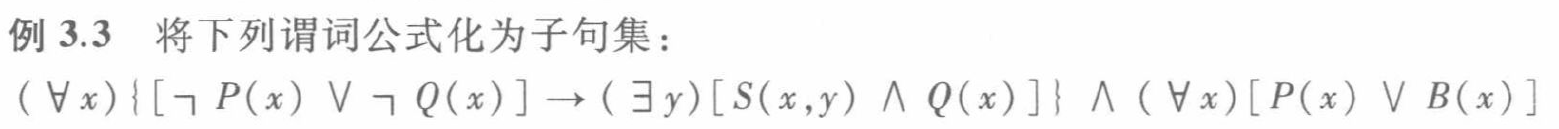
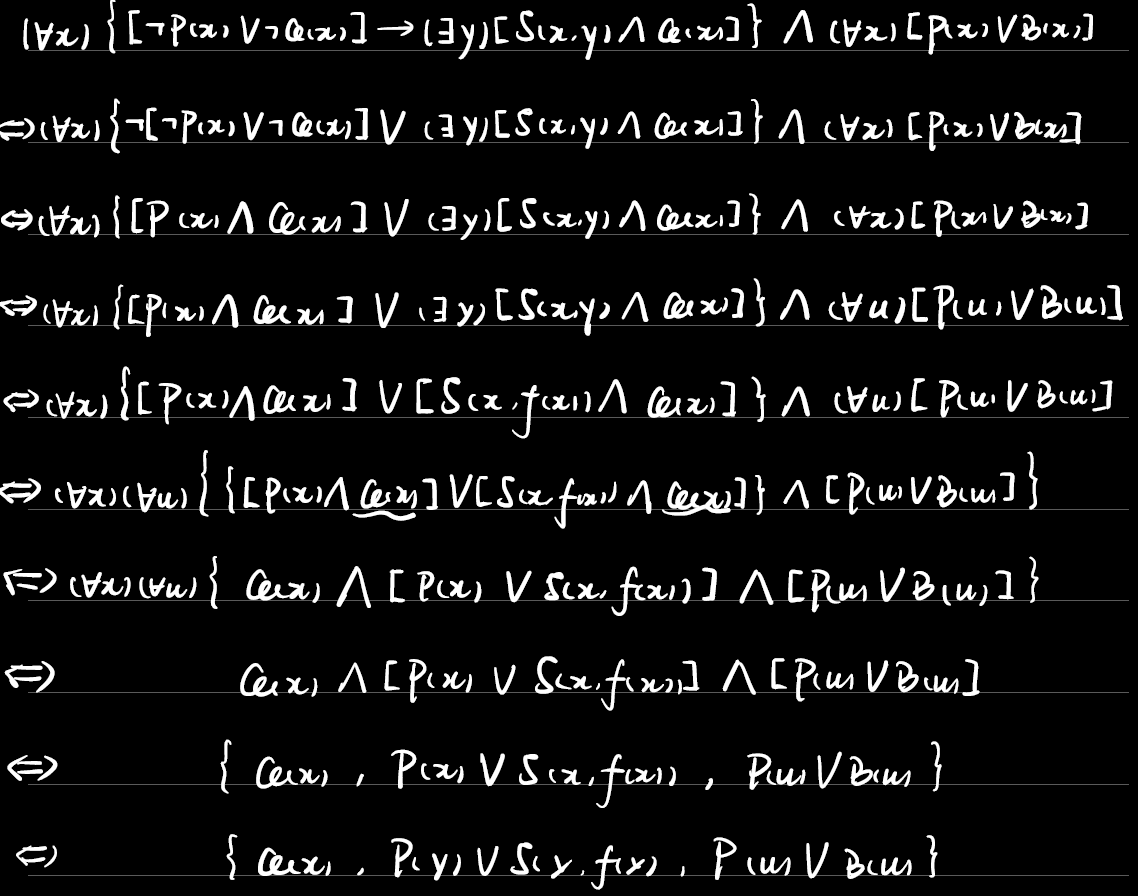
例3.4

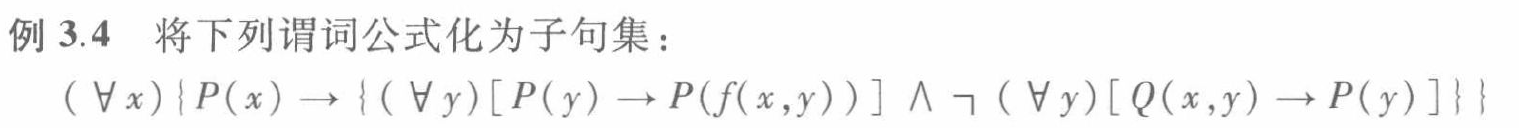
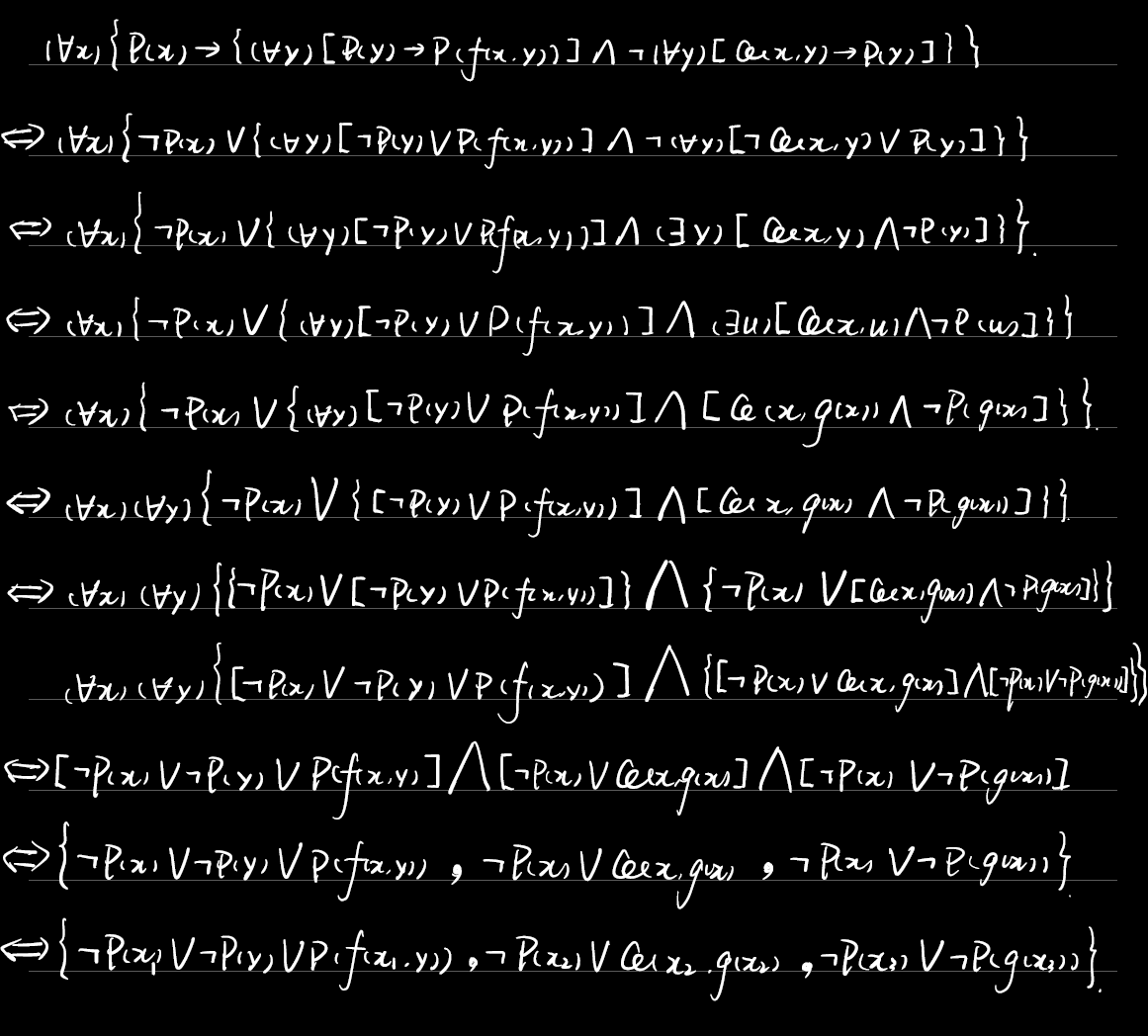
例3.5

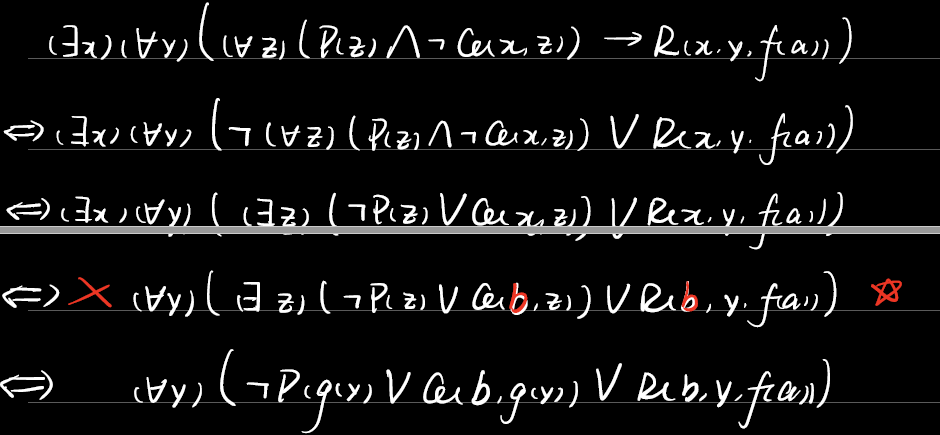
谓词公式不可满足$\Leftrightarrow$其子句集不可满足

鲁宾孙归结原理

命题逻辑中的归结原理

归结：

它类似直接把两式析取，但和析取的真值表不同。

定理：

推论：

归结出的结论把亲本换掉形成的$S_1$，或者直接塞进原子句集形成的$S_2$，对每一个而言，若它不满足则S不满足。

谓词逻辑中的归结原理

最一般合一

相当于$x \cdot a/x = a$，乘了$\sigma$就把$x$全换成$a$

归结：

若$C_1$和$C_2$中没有相同变元（若有则要改名）、$C_1$和$C_2$中没有可合一子句（若有则要先合一）

则

例3.6

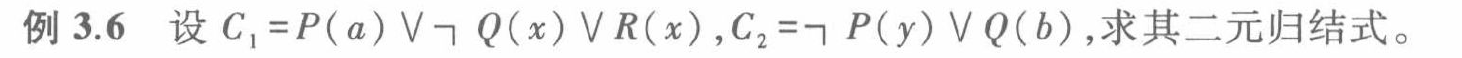
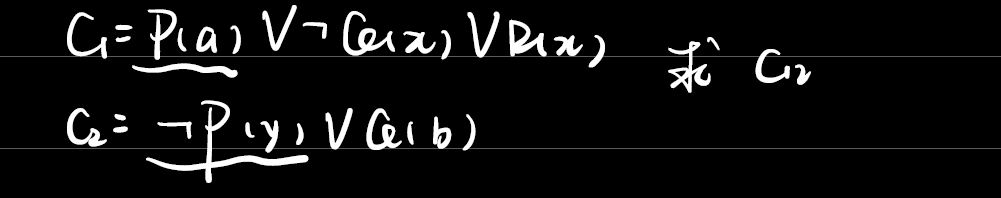
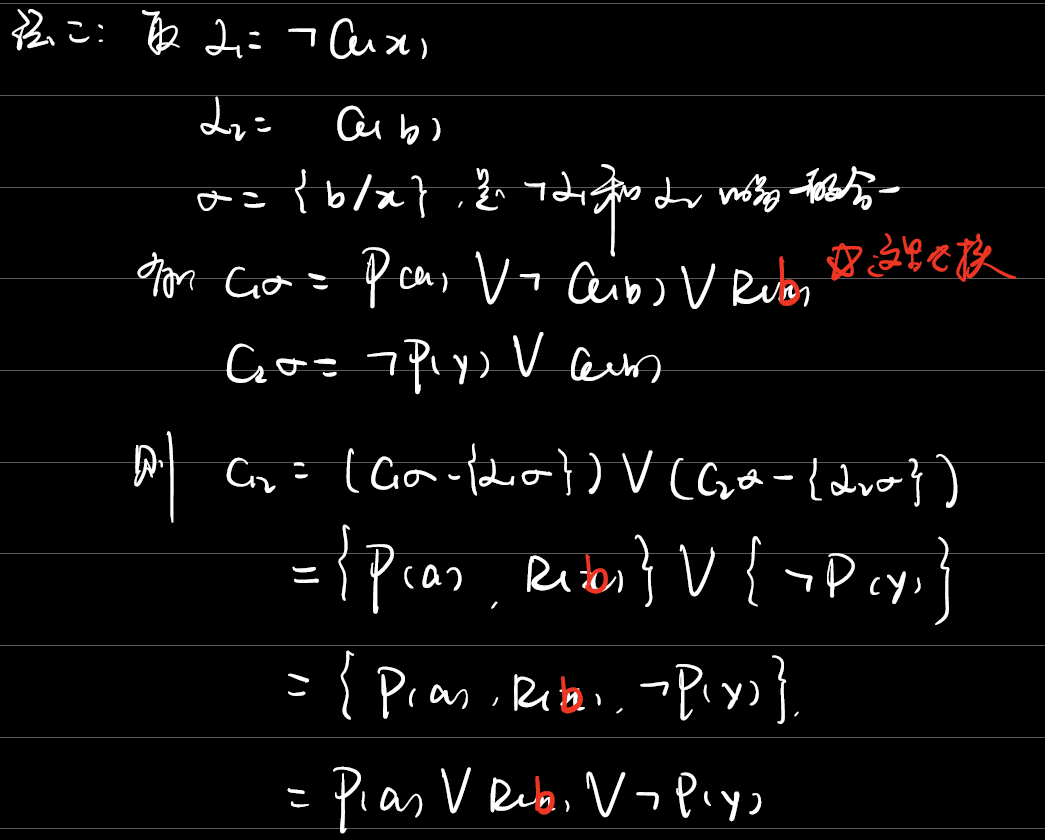
例3.7

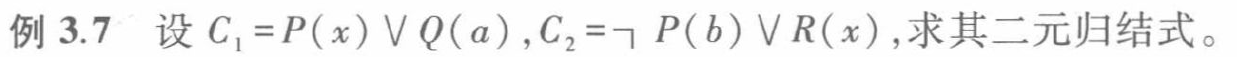
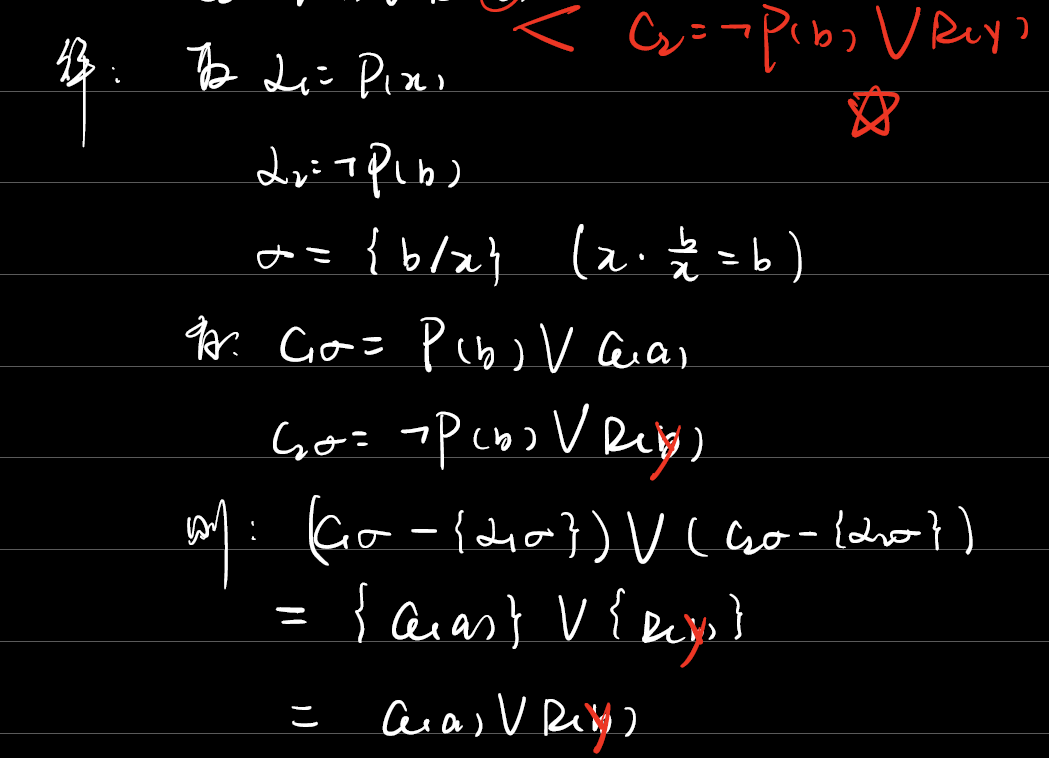
例3.8

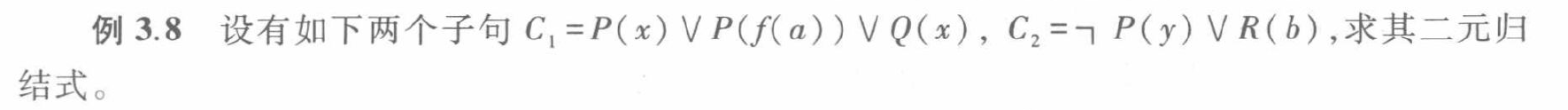
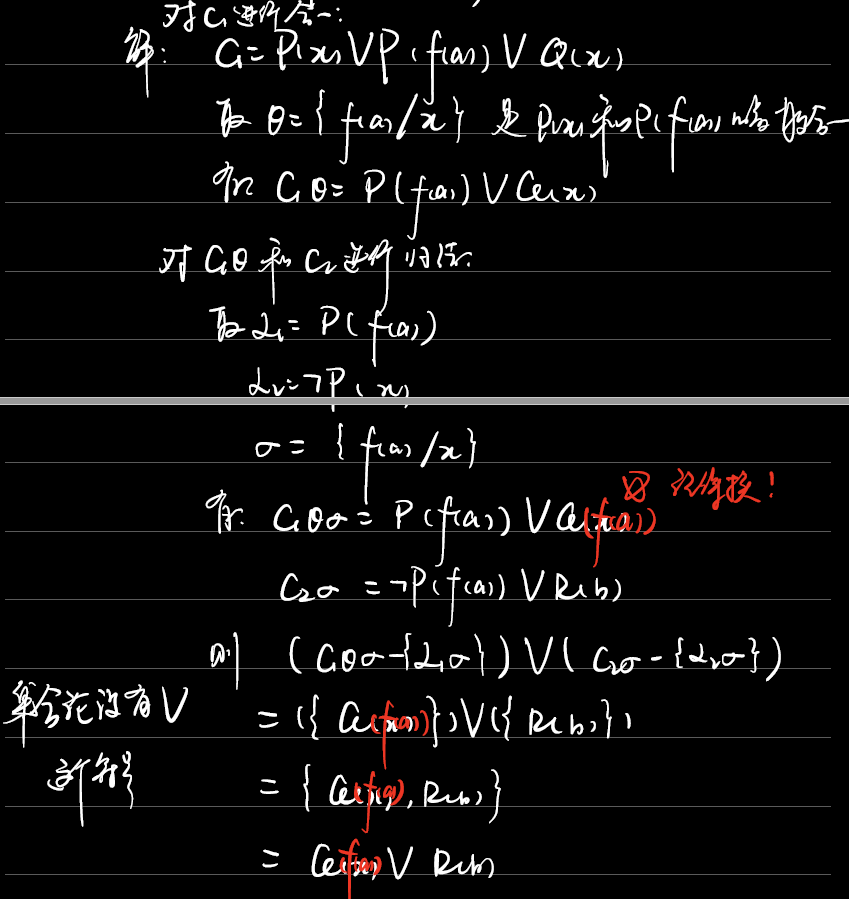
因子：$C\sigma$是$C$的因子

单元因子：$C\sigma$是一个单文字

归结反演（证明）

如果没有归结出空子句，则无法确定S是否可满足。

用之前的反证法，把结论的否定塞进谓词公式集

例3.9

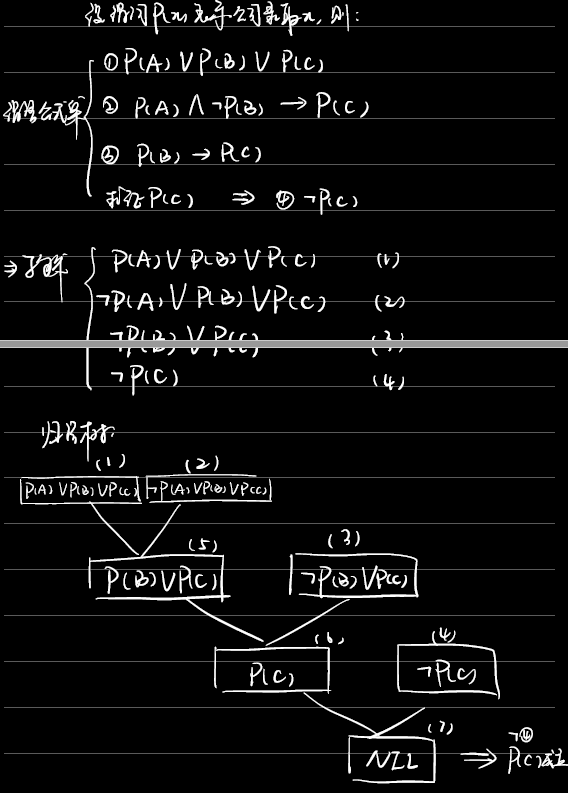
例3.10

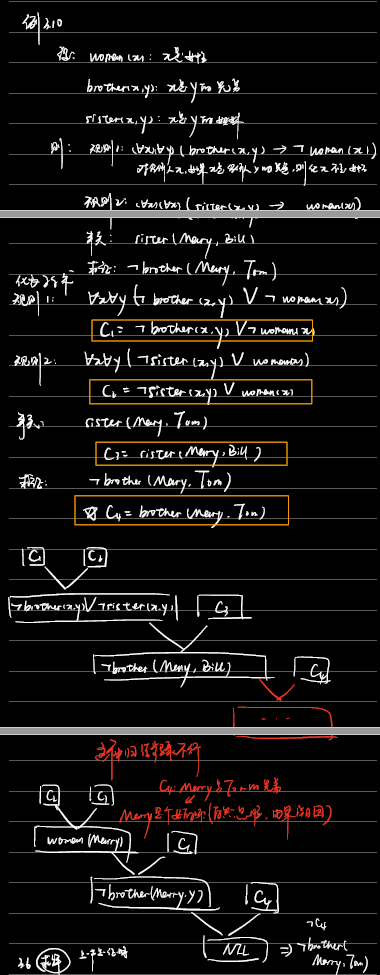
求解

把问题的否定 析取 $ANSWER(variable)$得到$\neg G \vee ANSWER(variable)$，然后将其扔到谓词公式集。

例3.11

例3.12

习题

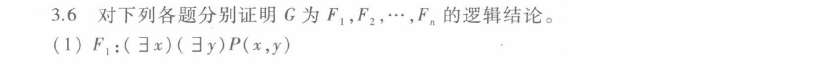
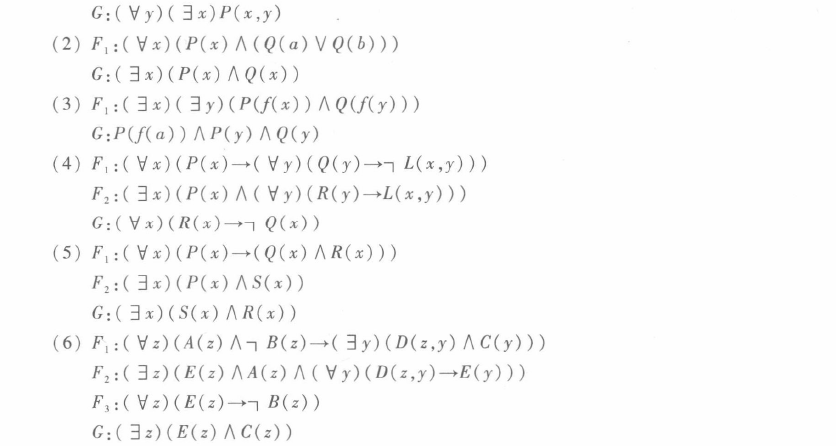
3.1 注意$B,C \Rightarrow B\wedge C$这一步要写出来。

3.2 注意量词的消去规则：从左往右看，逐次缩小域。存在量词若无”$\forall$”约束，则换为常量$a,b,c,\dots$；若有”$\forall variables$”，则换为$skolem$函数$f(variables),g(variables),h(variables),\dots$。

3.4 (3)、(4) 注意谓词连接词的优先级：$\neg \wedge \vee \rightarrow \leftrightarrow$

3.4 (6) 变元太多，可以用大括号把要替换的变元都写出来，然后直接写答案。

3.6 (2) 这里答案很奇怪，我认为是他错了。

3.6 (6) 子句很多，不容易归结。注意$a$和$f(a)$不能合一。

3.7 对于这种复杂的证明，要尽可能多地、更准确地设出谓词公式，包括作用的对象，比如$Dolphin(x)$：$x$是海豚。

3.8、3.9：注意结论$G$的表示：

“没有人去储蓄钱”应为$(\forall x)(\forall y)(Money(y)\rightarrow\neg Save(x,y))$，意为：对于任意x、任意y，如果y是钱，那么没有x去储蓄钱y。

“不会有人使用Internet”应为$(\forall x)(\forall y)(Internet(y)\rightarrow\neg Use(x,y))$，意为：对于任意x、任意y，如果y是Internet，那么不会有x使用Internet y。

不确定性推理方法

知识的静态强度：知识的不确定性程度

知识的动态强度：证据的不确定性程度

可信度方法

可信度方法：根据经验对一个事物或现象为真的相信程度。

知识不确定性的表示

C-F（Certainty-Factor）模型中的知识：

其中$CF(H, E)$称可信度因子（certainty factor），是当前提条件$E$为真时，对结论$H$的支持程度。

$CF(H, E) \in [-1,1]$时：小于0代表E支持H为假，等于0代表E与H无关，大于0代表E支持H为真，绝对值越大越支持。

证据不确定性的表示

$CF(E)=x$：E的可信度为x

静态强度$CF(H, E)$：表示当E对应的证据为真时对H的支持程度

动态强度$CF(E)$：E当前的不确定程度

组合证据不确定性的算法

当组合证据是多个单一证据的合取时，即：

若$CF(E_1), CF(E_2), \dots CF(E_n)$已知，则：

其实很好理解，如果一个人对你说了关于某一件事的观点和得到这个观点的n个小观点，当你认为其中一个小观点不太可信时，那你就会认为他对这件事的观点不太可信。

当组合证据是多个单一证据的析取时，即：

若$CF(E_1), CF(E_2), \dots CF(E_n)$已知，则：

同样地，n个人对你说了关于某一件事的n个观点，你会相信这n个观点里最可信的一个作为对这件事的观点。

注：理解部分只是暂时写一下，有时间再修改润色。

不确定性的传递算法

就是从$CF(E)\in[-1, 1]$映射到$CF(H)\in[0,1]$。

结论不确定性的合成算法

若由多条不同知识推出了相同的结论，但可信度不同，则可用合成算法求出综合可信度

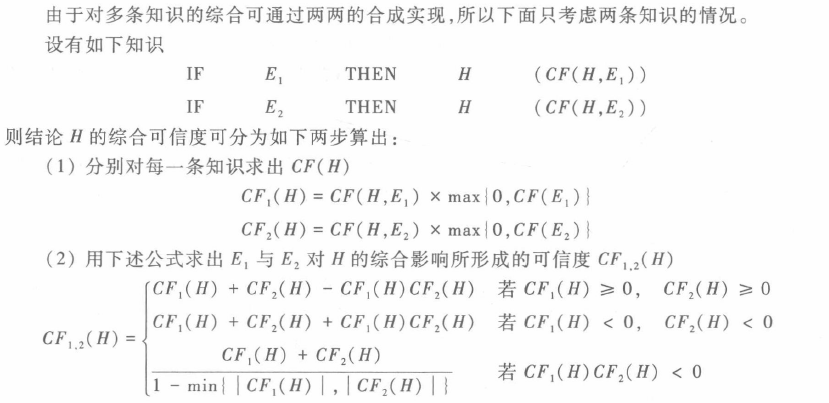
这个公式其实也很好记，综合可信度$C_{12}$是由$CF_1(H)+CF_2(H)$向0靠近得来的（将$CF_1(H)+CF_2(H)$的绝对值变小）。

对于1. $CF_1(H)+CF_2(H)$为正，$CF_1(H)CF_2(H)$为正，正-正靠近0

对于2. $CF_1(H)+CF_2(H)$为负，$CF_1(H)CF_2(H)$为正，负+正靠近0

对于3. $CF_1(H)+CF_2(H)$不确定，但分母是1-较小值=较大值，所以分式是绝对值较小值

例4.1

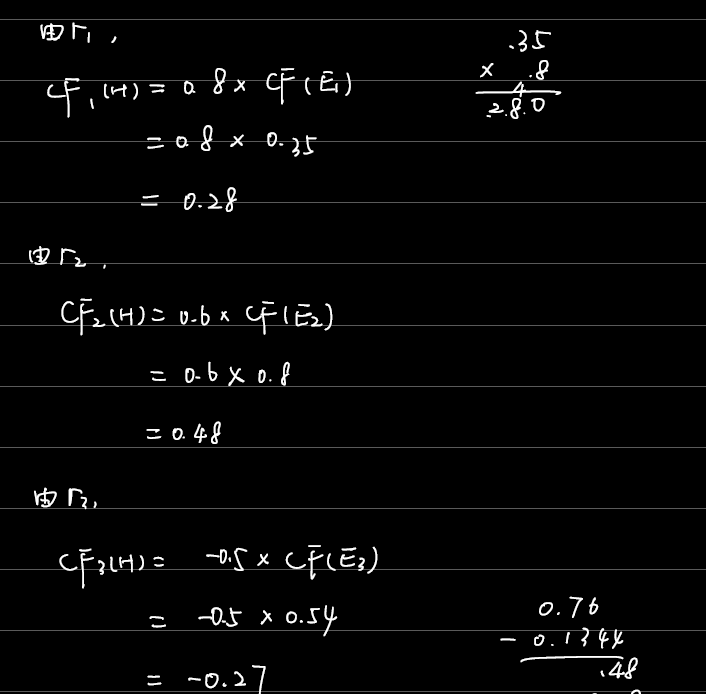
证据理论

概率分配函数

设D为样本空间，D中元素互斥，领域中的命题都用D的子集表示。

基本概率分配函数（Basic Probability Assignment Function）$M:2^D\rightarrow[0,1]$，即对任何一个属于D的子集A，映射到一个数$M\in [0,1]$，且满足：

则称$M$是$2^D$上的基本概率分配函数，$M(A)$称为$A$的基本概率数。

信任函数

信任函数（Belief Function）$Bel:2^D\rightarrow[0,1]$，且：

Bel函数又称下限函数，Bel(A)表示对命题A为真的总信任程度。

似然函数

似然函数（Plausibility Function）$Pl:2^D\rightarrow[0,1]$，且：

Pl函数又称上限函数、不可驳斥函数，Pl(A)表示对命题A为非假的总信任程度。

M正交和

设$M_1$和$M_2$是两个基本概率分配函数，其正交和$M=M_1\oplus M_2$为：

不确定性推理

例4.3

模糊推理方法

模糊集合（fuzzy sets）

论域（Domain of discourse）：所讨论的全体对象称为域。

元素（Element）：论域中的每个对象。

集合（Set）：论域中具有某种相同属性的、确定的、可以彼此区别的元素的全体。

隶属度（Degree of Membership）：描述模糊集合中的每一个元素属于这个模糊集合的强度的一个介于0到1之间的实数。

隶属函数（Membership function）：模糊集合中所有元素的隶属度全体。

表示方法：

  1. Zadeh表示法：

    离散：

    \\和+/$\sum$分别表示分隔符、模糊集合整体。

    连续：

    $\int$表示模糊集合整体。

  2. 序偶表示法：

  3. 向量表示法：

模糊集合的运算

包含：若$\mu_A(x)\geq \mu_B(x)$，则$A\supset B$

相等：若$\mu_A(x)= \mu_B(x)$，则$A= B$

交：$\mu_{A\cap B}(x)=min\{\mu_A(x), \mu_B(x)\}=\mu_A(x)\wedge\mu_B(x)$

并：$\mu_{A\cup B}(x)=max\{\mu_A(x), \mu_B(x)\}=\mu_A(x)\vee\mu_B(x)$

补：$\mu_{\overline{A}}(x)=1-\mu_A(x)$

代数积：$\mu_{A\cdot B}(x)=\mu_A(x)\mu_B(x)$

代数和：

有界和：$\mu_{A\oplus B}(x) = min\{1,\mu_A(x)+\mu_B(x)\}$

有界积：$\mu_{A\otimes B}(x) = max\{0,\mu_A(x)+\mu_B(x)-1\}$

注：下方的$\mu$和$R$应为粗体，代表向量和矩阵，我暂时不会打。

叉积：$R = \mu_{A\times B}(a,b) = \mu_A^\mathrm{T}\circ\mu_B$

$\circ$为模糊向量最小乘积

模糊关系R合成：$S = Q \circ R$

$\circ$有两种常用计算方法：

  1. 最小-最大合成法：在矩阵乘法的基础上，将乘积换为取小、求和换为取大；
  2. 代数积-最大合成法：在矩阵乘法的基础上，将乘积换为代数积、求和换为取大。

模糊推理

模糊知识表示：

模糊规则推理：

已知$A$、$B$、$A’$，求$B’$

模糊决策

模糊决策：将模糊推理得到的模糊向量转化为确定值的过程。

  1. 最大隶属度法

  2. 加权平均判决法

  3. 中位数法

    注：可以先计算sum/2，当累加到最接近该值的$\mu(u_i)$时，$U = u_i$。

综合应用

例4.10

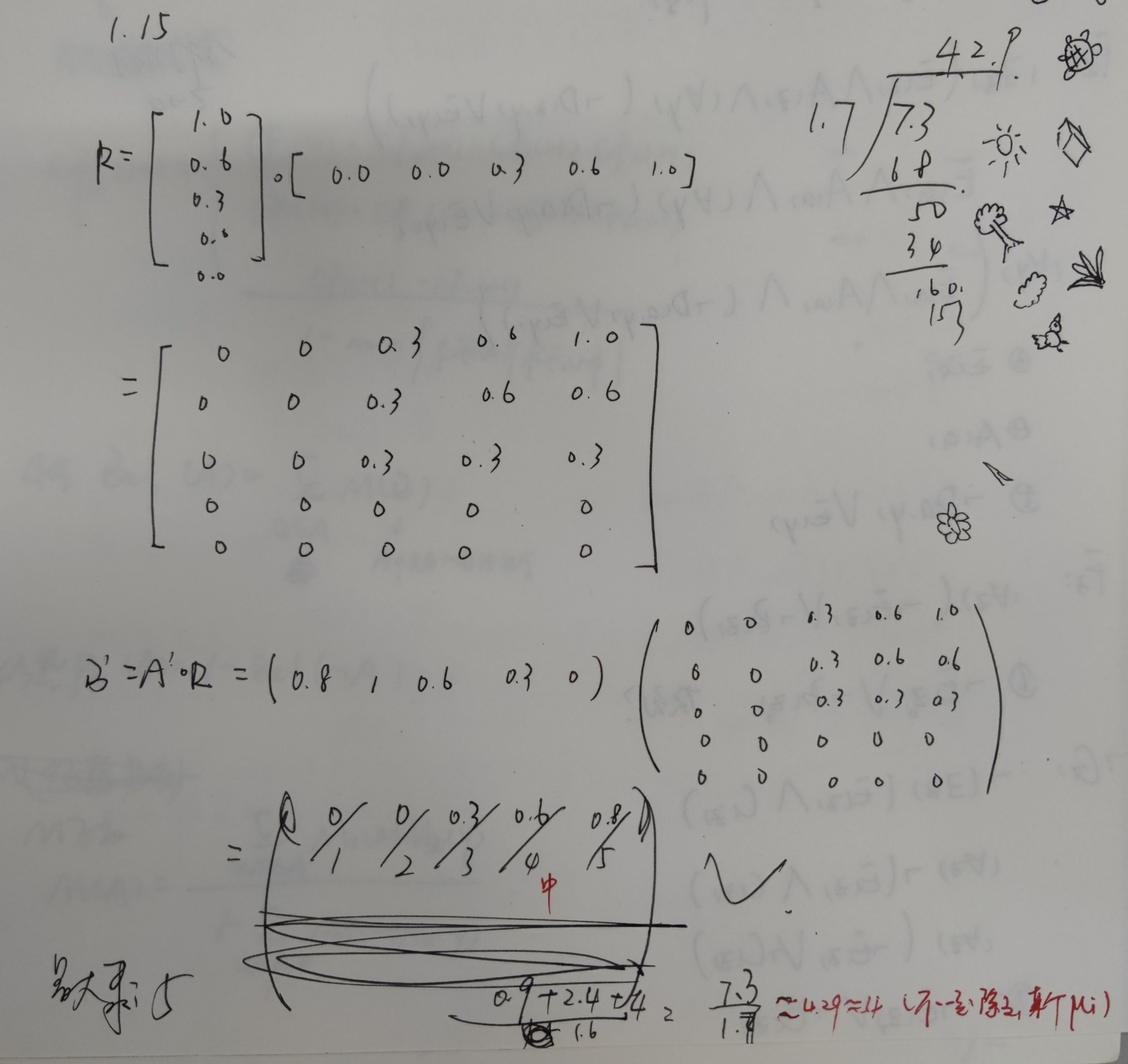
注：右边是女朋友画的。

习题

4.2 初始可信度需要参与合成。

4.3 本题中的推理网络还蛮好用，不过没在正文中出现。

4.9 极小-极大算法可以用“打擂法”在脑中遍历一次直接得出结果。

搜索求解策略

搜索的概念

盲目搜索（Blind search）：在对特定问题不具有任何有关信息的条件下，按固定的步骤（依次或随机调用操作算子）进行的搜索。

启发式搜索（Heuristic search）：考虑特定问题领域可应用的知识，动态地确定调用操作算子的步骤，优先选择较合适的操作算子，以求减少不必要的搜索、尽快达到结束状态、提高搜索效率的搜索。

状态空间的搜索策略

状态空间：利用状态变量和操作符号，表示系统或问题的有关知识的符号体系。

$S$：状态集合

$O$：操作算子的集合

$S_0$：初始状态

$G$：目的状态

求解路径：从$S_0$结点到$G$结点的路径

解：求解路径上的操作算子序列

盲目的图搜索策略

回溯策略

回溯（Backtracking）

数据结构：

路径状态表（Path States Table, PS）：保存当前搜索路径上的状态。

新的路径状态表（New Path States Table, NPS）：保存等待搜索的状态。

不可解状态表（No Solvable States Table, NSS）：保存找不到解路径的状态。

当前正在被遍历的状态（Current State, CS）：当前正在被遍历的状态（hhhh废话）。

宽度优先搜索策略

宽度优先搜索（Breadth-First Search）

数据结构：

open表：NPS表，保存已生成但未被遍历的状态。

closed表：PS表和NSS表，保存已遍历的状态。

Pascal伪代码描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Procedure breadth_first_search
begin
open := [S0];			// 队列
closed := [];			// 栈
while open != [] do
	begin
		从open表中删除第一个状态，赋给n;
		将n放入closed表中;
		if n = G then return (success);
		生成n的所有子状态;
		从n的所有子状态中删除已在open表或closed表中出现的状态;
		将n的剩余子状态，按生成次序加入open表的后段;
	end;
end;

深度优先搜索策略

深度优先搜索（Depth-First Search）

数据结构：

open表：NPS表，保存已生成但未被遍历的状态。

closed表：PS表和NSS表，保存已遍历的状态。

Pascal伪代码描述：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Procedure breadth_first_search
begin
open := [S0];			// 栈
closed := [];			// 栈
while open != [] do
	begin
		从open表中删除第一个状态，赋给n;
		将n放入closed表中;
		if n = G then return (success);
		if n的深度 < depth_limit then continue;
		生成n的所有子状态;
		从n的所有子状态中删除已在open表或closed表中出现的状态;
		将n的剩余子状态，按生成次序加入open表的前段;
	end;
end;

注：这一节书上讲的很差，建议去算法方面的书学习这里。我要是还有时间会补这里的。

启发式图搜索策略

启发式策略

启发式策略利用启发信息引导搜索。

启发信息：与问题有关的信息。

例5.6 井字棋

采用启发式策略，搜索树如下：

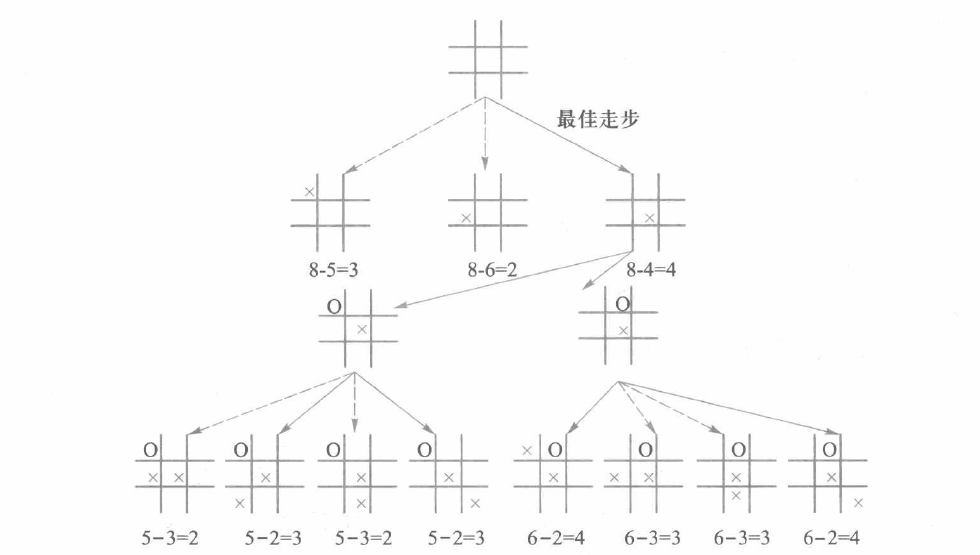
其实这种启发式策略很简单，就是将净赢状态数作为启发值，搜索启发值最大的那个/那些状态。

以第一步为例（X方回合）：

首先缩减状态空间，可以看出共有3种不同的落子处（类似魔方中的角块、棱块、中心块）。

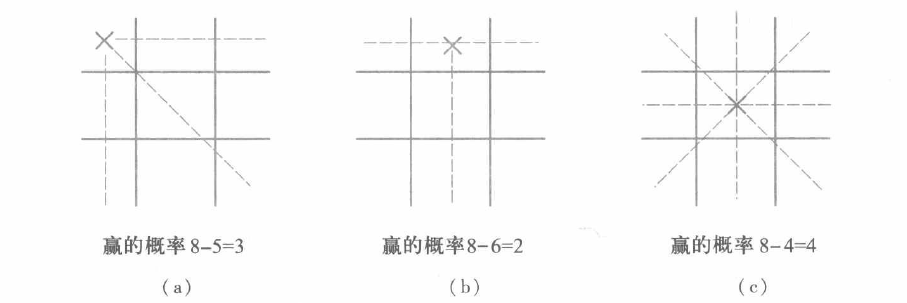
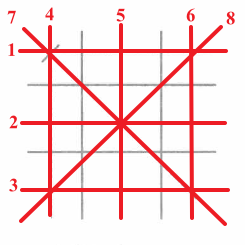
既然井字棋的规则是只要没被对方棋占住的空格就都可以下，那么以(a)图为例，X方的赢状态数共有8种。

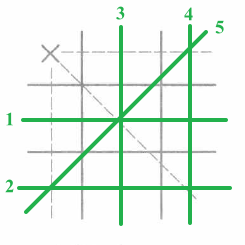
那么下完这步后，O方的赢状态数共有5种。

所以X方若下在角块处，净赢状态数共有8-5=3种，而下在中心块有8-4=4种，所以依启发式策略，第一步搜索了X方下在中心块的状态。

启发信息和估价函数

A搜索算法

A*搜索算法

智能计算及其应用

注：这一章后面就进入机器学习部分了，所以到这里人工智能的基本知识就结束了，后面看西瓜书就可以了。